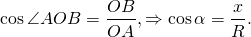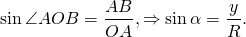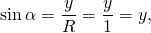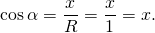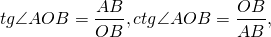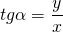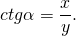Ордината точки единичной окружности не может быть равна

Геометрия | 5 — 9 классы

Может ли ордината точки единичной полуокружности иметь значения 0, 6 ; 1 / 7 ; — 0, 3 ; 7 ; 1, 002 ?

1 / 7 — может — 0, 3— может

Все числа, которые больше нуля, не могут быть значениями в единичной окружности, ибо радиус единичной окружности равен 1.

Видео:Тригонометрическая окружность. Как выучить?Скачать

Помогите пожайлуста решить?

Помогите пожайлуста решить!

Точка (1 / 2 ; корень из 3 делить на 2) лежит на единичной полуокружности Синус угла MOX.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Как расположена единичная полуокружность в системе координат?

Как расположена единичная полуокружность в системе координат?

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Найдите синус, косинус и тангенс угла АОМ, если О — начало координат, а точки А(1 : 0), М( — 1 / 5 : у) лежат на единичной полуокружности?

Найдите синус, косинус и тангенс угла АОМ, если О — начало координат, а точки А(1 : 0), М( — 1 / 5 : у) лежат на единичной полуокружности.

Видео:Изобразить на единичной окружности точку.Скачать

Выясните принадлежит ли полуокружности точки?

Выясните принадлежит ли полуокружности точки.

Видео:9 класс, 9 урок, Синус, косинус, тангенс, котангенсСкачать

Принадлежит ли единичной полуокружности точка : а) ( — 0, 6 ; 0, 8)?

Принадлежит ли единичной полуокружности точка : а) ( — 0, 6 ; 0, 8)?

Видео:Как искать точки на тригонометрической окружности.Скачать

Ордината точки, лежащей на единичной окружности, — это : ?

Ордината точки, лежащей на единичной окружности, — это : .

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать

Касательная к графику функции y = X ^ 2 — 2x + a, в точке с абциссой x = 3 пересекает ось ординат, в точке с ординатой » — 6″?

Касательная к графику функции y = X ^ 2 — 2x + a, в точке с абциссой x = 3 пересекает ось ординат, в точке с ординатой » — 6″.

Найдите значение параметра а.

Видео:Как найти координаты точек на тригонометрической окружностиСкачать

Найдите синус, косинус и тангенс угла BOP, если О — начало координат, а точки В(1 ; 0) и P ( — 3 / 4 : y) лежат на единичной полуокружности?

Найдите синус, косинус и тангенс угла BOP, если О — начало координат, а точки В(1 ; 0) и P ( — 3 / 4 : y) лежат на единичной полуокружности.

Видео:Тригонометрическая окружность для непонимающихСкачать

Какое из значений не может иметь ордината точки M на единичной полуокружности?

Какое из значений не может иметь ордината точки M на единичной полуокружности.

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Какое из значений не может иметь абсцисса точки М на единичной окружности?

Какое из значений не может иметь абсцисса точки М на единичной окружности?

На этой странице находится вопрос Может ли ордината точки единичной полуокружности иметь значения 0, 6 ; 1 / 7 ; — 0, 3 ; 7 ; 1, 002 ?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 5 — 9 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

Симметрия — это соответствие, неизменность, которая проявляется при каких — либо изменениях.

РЕШЕНИЕ Формула боковой поверхности конуса S = π * R * L, где L — образующая конуса. — гипотенуза прямоугольного треугольника. Образующая — L — катет при угле 45° L = √2 * R = 5√2 И находим площадь S = π * 5 * 5 * √2 = 25√2 * π — ОТВЕТ Рисунок — в ..

Надеюсь что понятно.

R = a / корень из 2 — формула нахождения радиуса описанной окружности. А — сторона квадрата R = 8 * корень из 2 / корень из 2 = 8 (сокращаем корни).

А)Около четырехугольника можно описать окружность, если суммы углов равны 180°. По теореме косинусов из треугольника АВС : АC2 = AB2 + CB2–2·AB·CB·cos∠B 49 = 9 + 25–30·cos∠B cos∠B = 15 / (–30) = –1 / 2 По теореме косинусов из треугольника АDС : АC2 ..

Решение : A = B 180 — (56 + 56) = 68.

Квадратный корень из 3 * 3 + 5 * 5 9 + 25 = 34 корень из 34 (клеток).

S = (8×11) / 2 = 44 Площадь равна полупроизведению двух катетов.

Трапеция прямоугольная, Углы А и В по 90 градДиагональ ВД является основанием равнобедренного тре — ка ВДС (по усл)Углы при основании будут равныПоскольку в трап основания параллельны, то диагональ ВД — секущая, углы СВД и ВДА противолежащие и равные..

АВС — рівнобедрений трикутник, у якого АВ = ВС = 50 ; ВК⊥АС. За умовою ВК = х ; АС = 1, 5х ; АК = 0, 75х. ΔАВК. АК² + ВК² = АВ² ; (0, 75х)² + х² = 2500 ; х² = 1600 ; х = 40 ; ВК = 40 см ; АС = 1, 5·40 = 60 см. S(АВС) = 0, 5ВК·АС = 0, 5·40·60 = 12..

Видео:9 класс. Геометрия. Тригонометрические функции угла от 0° до 180°. Единичная окружность. Урок #1Скачать

Единичная окружность

Что такое единичная окружность и как с ее помощью вводятся определения синуса, косинуса, тангенса и котангенса?

Рассмотрим в прямоугольной декартовой системе координат окружность с центром в начале координат — точке O.

Отметим на окружности точку P, лежащую на оси абсцисс справа от точки O.

Осуществим поворот радиуса OP около точки O на угол α в верхнюю полуплоскость.

При этом радиус OP займет положение OA. Говорят, что при повороте на угол альфа радиус OP переходит в радиус OA, а точка P переходит в точку точку A(x;y).

Опустив перпендикуляр AB из точки A на ось Оx, получим прямоугольный треугольник OAB, в котором гипотенуза OA равна радиусу окружности, катеты AB и OB — ординате и абсциссе точки A: OA=R, AB=y, OB=x.

Катет AB — противолежащий углу AOB, равному α, катет OB — прилежащий.

По определению косинуса острого угла в прямоугольном треугольнике,

Таким образом, на окружности косинус угла α — это отношение абсциссы точки A окружности к радиусу этой окружности.

Аналогично, по определению синуса острого угла в прямоугольном треугольнике,

Значит, синус угла α — это отношение ординаты точки A окружности к радиусу этой окружности.

Для окружности любого радиуса отношения x/R и y/R не зависят от величины радиуса, а зависят только от угла альфа. Поэтому удобно взять R=1. Для окружности единичного радиуса определение синуса и косинуса упрощаются:

Окружность с центром в начале координат и радиусом, равным единице, называется единичной окружностью.

Отсюда получаем определения синуса и косинуса на единичной окружности.

Синусом угла α называется ордината точки A единичной окружности, полученной при повороте точки P(1;0) на угол α.

Косинусом угла α называется абсцисса точки A единичной окружности, полученной при повороте точки P(1;0) на угол α.

Применив определения тангенса и котангенса острого угла в прямоугольном треугольнике в ∆AOB, получаем:

Приходим к определению тангенса и котангенса на единичной окружности.

Тангенсом угла α называется отношение ординаты точки A единичной окружности к абсциссе этой точки.

Котангенсом угла α называется отношение абсциссы точки A единичной окружности к ординате этой точки.

Видео:10 класс. Косинусы и синусы вершин тригонометрической окружностиСкачать

One Comment

Искала везде. Нигде нет такого подробного и понятного объяснения. Огромное Вам спасибо!

Видео:6 Линия тангенсов и линия котангенсовСкачать

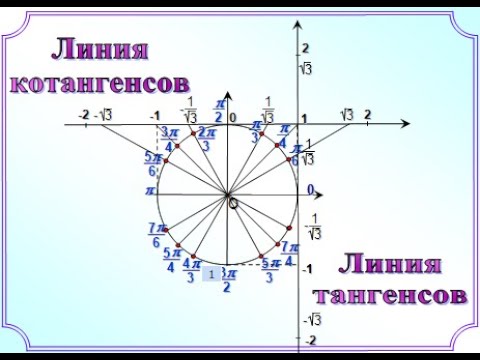
Информационные технологии на уроках математики

Разделы: Математика

Тема урока: Определение синуса и косинуса угла.

Цели урока:

• ввести определение синуса и косинуса любого угла; отработать алгоритм нахождения синуса и косинуса на числовой окружности;
• развивать логическое мышление, умение обобщать.
• воспитывать самостоятельность, ответственность, творческое отношение к деятельности.

Тип урока: объяснения нового материала сопровождается показом презентации. (Приложение 1)

Формы работы: фронтальный опрос, фронтальное обсуждение и решение у доски.

Оборудование: компьютер, проектор, экран, шарнирная модель с изображением на миллиметровой бумаге окружности большого радиуса, на которой нанесены градусные меры с шагом в 30 градусов, и с подвижным радиусом, чертежные инструменты.

1. Приветствие

Сообщение темы и целей урока.

2. Введение в атмосферу урока

Показ учебной презентации с помощью видеопроектора. (Слайд 1)
Запишите тему урока: «Определение синуса и косинуса угла». Как называется раздел математики, зашифрованный в ребусе. (Слайд 2)
Ответ: Тригонометрия.
Слово “тригонометрия” (от греческих слов “тригонон” – треугольник и “метрео” – измеряю) означает “измерение треугольников”. Возникновение тригонометрии связано с развитием астрономии – науки о движении небесных тел, о строении и развитии Вселенной. (Слайд 3)

3.Фронтальный опрос

Вы уже знакомы с понятием синус и косинус и можете найти синус и косинус углов, радианная мера которых заключена между 0 и . (Слайд 4). Найдите cos150 о ; sin45 о ; sin0 о ; sin30 о ; sin120 о ; cos135 о ; cos90 о ; cos60 о .

4. Объяснение нового материала

А как найти значение sin240 о и cos240 о ? Как определить синус и косинус любого угла? (Слайд 5)
Для этого рассмотрим прямоугольную систему координат и окружность единичного радиуса с центром в начале координат. Пусть подвижный вектор, совершив поворот от вектора ОА до вектора ОВ, образовал угол АОВ, радианная мера которого равна радиан. Точку В назовем точкой, соответствующей углу , или коротко, точкой . Заметим, что если точка В соответствует числу , то она соответствует и всем числам вида + 2к, где к – целое число. Положение точки В будет определяться углом поворота с одной стороны, с другой стороны координатами (X; Y) в прямоугольной системе координат. (Слайд 6)
Какая связь между координатами (X; Y) и углом поворота А?

Учащиеся делают вывод: X = cos А; Y = sin ?. (Слайд 7)

Определение: Число, равное ординате точки единичной окружности, соответствующей углу , называют синусом угла . Число, равное абсциссе точки единичной окружности, соответствующей углу , называют косинусом угла . (Слайд 8)

Из сказанного выше следует, что для любого угла существует и притом единственный синус и косинус, значит синус и косинус являются функциями угла.

Пример 1: Найдем значение sin240 о и cos 240 о . Для этого:

1. На числовой окружности найдем точку, соответствующую углу поворота 240 о .
2. Найдем координаты этой точки.
3. X = cos240 о ; Y = sin240 о . (Слайды 9, 10)

5. Закрепление

Учащиеся на доске. № 7.31. Найдите cos0 о ; sin0 о ; cos270 о ; sin270 о .

Показать, как заполняется таблица значений тригонометрических функций аргументов от 0 до 2 о . Для этого рассмотреть прямоугольный треугольник с гипотенузой, равной 1. Для точки /4 все сводится к рассмотрению равнобедренного прямоугольного треугольника. Его катеты равны 2/2, 2/2; значит, координаты точки /4 (2/2, 2/2) Аналогично обстоит дело с точками 3/4, 5/ 4, 7/4, но разница лишь в знаках абсциссы и ординаты. Запомните, что модули абсциссы и ординаты у середин всех четвертей равны 2/2, а знаки определяются по чертежу. (Слайд 11). Для точки /6 все сводится к рассмотрению прямоугольного треугольника с гипотенузой 1 и углом 30 о . Тогда катет, противолежащий углу 30 о будет равен 1/2 , а прилежащий катет равен 3/2 . Значит, координаты точки /6 (3/2, 1/2) . Для точки /3 (1/2, 3/2). (Слайд 12)

6. Беседа по вопросам

1. Какую окружность в тригонометрии называют единичной окружностью?
Ответ: Единичной окружностью в тригонометрии называют окружность радиуса 1 с центром в начале координат.

2. Какую точку единичной окружности называют точкой, соответствующей углу ?
Ответ: точку В назовем точкой, соответствующей углу , если подвижный вектор, совершив поворот от вектора ОА до вектора ОВ, образовал угол АОВ, радианная мера которого равна радиан.

3. Какая связь между координатами (X; Y) и углом поворота ?
Ответ: Абсциссу х называют косинусом числа , а ординату y называют синусом числа .

4. Почему синус и косинус являются функциями угла?
Ответ: Синус и косинус являются функциями угла, потому что для любого угла существует и притом единственный синус и косинус.

5. Какие значения могут принимать синус и косинус?
Ответ: Синус и косинус принимают значения от –1 до 1.

6. Синус и косинус имеют одинаковые знаки, в какой четверти находится угол?
Ответ: Синус и косинус положительны в первой четверти и отрицательны в третьей четверти.

7. Подведение итогов, домашнее задание: П.7.3. № 7.33–7.35.

📺 Видео

Знаки тригонометрических функций на единичной окружности. Тригонометрия 8-11 класс.Скачать

Синус, косинус произвольного угла. 9 класс.Скачать

ЗНАЧЕНИЯ СИНУСА И КОСИНУСА НА ОКРУЖНОСТИСкачать

Определение синуса косинуса тангенса котангенса на единичной окружности. Шпаргалка по тригонометрииСкачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

3 Единичная окружность на координатной плоскости 10 классСкачать