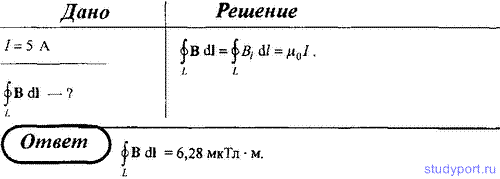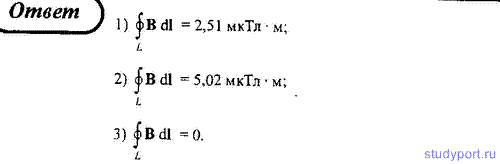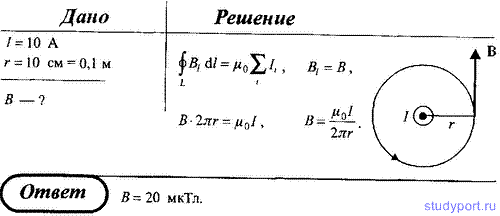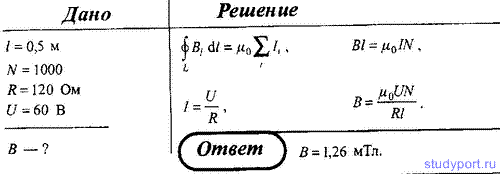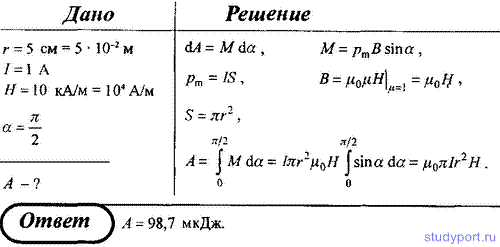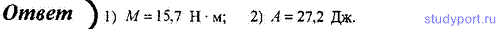Определить циркуляцию вектора магнитной индукции по окружности (7 видео)

Определить циркуляцию вектора магнитной индукции по окружности

2.3. Циркуляция вектора магнитной индукции

2.3.1. Теорема о циркуляции вектора магнитной индукции

Связь между током и магнитным полем, образованным этим током, устанавливает эмпирический закон Био — Савара — Лапласа. Еще одной из форм связи является теорема о циркуляции вектора магнитной индукции.

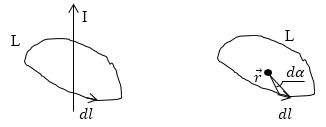
Возьмем контур l (рис. 2.3.1), охватывающий прямой ток I, и вычислим для него циркуляцию вектора магнитной индукции B, т.е. .

Вначале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В каждой точке контура вектор B направлен по касательной к окружности, проходящей через эту точку (линии B прямого тока — окружности).

Воспользуемся свойствами скалярного произведения векторов.

. — проекция dl на вектор B, но . где R — расстояние от прямой тока I до dl;

— это теорема о циркуляции вектора B: циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную.

Иначе обстоит дело, если ток не охватывается контуром (рис. 2.3.2).

Содержание

Теорема о циркуляции вектора индукции магнитного поля
Интегральная форма теоремы о циркуляции
Готовые работы на аналогичную тему
Дифференциальная форма теоремы о циркуляции
Магнитное поле
🎥 Видео

Видео:Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать

Теорема о циркуляции вектора индукции магнитного поля

Вы будете перенаправлены на Автор24

Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Интегральная форма теоремы о циркуляции

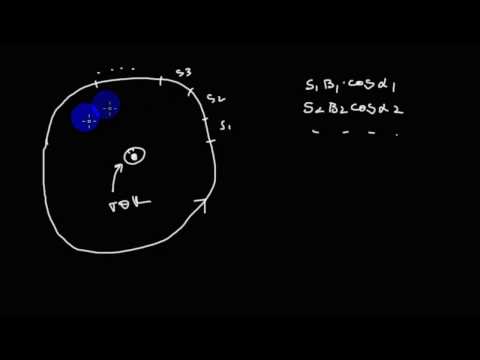
Линии индукции магнитного поля, которое возникает вокруг постоянного тока, который течет по прямолинейному длинному проводнику — концентрические окружности с центрами на линии тока. Интеграл вида $ointlimits_L<overrightarrowdoverrightarrow> $- циркуляция вектора $overrightarrow$ по замкнутому контуру L. Найдем $ointlimits_L<overrightarrowdoverrightarrow>$ по некоторому замкнутому контуру вокруг тока I (рис. 1).

Линии магнитной индукции лежат в плоскостях перпендикулярных линии тока I, контур L выбираем в плоскости одной из линий $overrightarrow.$ Используем рис.1, получим:

Обозначим $left(widehat<overrightarrowdoverrightarrow>right)=alpha $, тогда имеем:

По условию магнитное поле создает бесконечно длинный прямой проводник с током, индукцию поля которого мы знаем, и запишем в точке на расстоянии r от проводника как:

Подставим (3) и (2) в формулу (1), получим:

Теперь найдем циркуляцию вектора магнитной индукции, используя (4), получим:

где использовано то, что для замкнутого контура, который окружает начало координат:

Из полученного результата в (5) видим, что циркуляция вектора магнитной индукции по замкнутому контуру вокруг тока не зависит от вида контура и определена только силой тока. В том случае если контур ток не охватывает, то циркуляция вектора индукции равна нулю.

Тогда теорема о циркуляции для нескольких токов формулируется следующим образом:

Циркуляция индукции магнитного поля постоянных токов по произвольному замкнутому контуру равна алгебраической сумме токов, которые пронизывают этот контур.

Готовые работы на аналогичную тему

В математическом виде данная формулировка выглядит как уравнение:

где через I — обозначают полный ток (алгебраическая сумма всех токов, охватываемых контуром). Теорема о циркуляции еще называется законом полного тока. Надо иметь в виду, что циркуляция вектора $overrightarrow$ по замкнутому контуру равна нулю не только в случае отсутствия токов, которые пронизывают заданный контур, но и если токи текут в противоположных направлениях и в сумме дают ноль. В формуле (7) знак тока учитывается по правилу правого винта. Этот закон мы получили для прямого бесконечного проводника, но он справедлив и для произвольного тока.

Видео:Теорема о циркуляции вектора магнитной индукции. Магнитный поток.Скачать

Дифференциальная форма теоремы о циркуляции

Пусть S — поверхность, которую охватывает контур L. Положительная нормаль к поверхности связана с направлением обхода контура L правилом правого винта. Силу полного тока, который течет через поверхность S можно записать как:

где $overrightarrow$ — объёмная плотность тока. В таком случае теорему о циркуляции запишем как:

По теореме Стокса можно записать, что:

Равенство (11) выполняется для любой поверхности, следовательно, подынтегральное выражение также равно нулю:

[rotoverrightarrow-_0overrightarrow=0to rotoverrightarrow=_0overrightarrow left(12right).]

Равенство (12) дифференциальная форма теоремы о циркуляции. Она справедлива для произвольного поля в каждой точке.

Напомним, что теорема о циркуляции в виде (7) и (12) записана для поля в вакууме и стационарных токов.

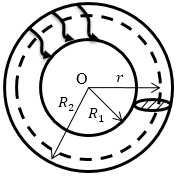
Задание: Тороид имеет каркас в виде тора и на него намотан проводник, по которому течет ток. Магнитное поле данной конфигурации токов сосредоточено в основном внутри тороида. Поле имеет осевую симметрию. Силовые линии магнитного поля тороида представляют собой окружности с центром на оси тороида. Используя теорему о циркуляции, найдите магнитное поле внутри тороида (рис.2) (B(r)). Если сила тока в нем равна I. N — число витков тороида.

В качестве контура циркуляции выберем силовую линию в виде окружности радиуса r (рис.2). Запишем, что циркуляция вектора индукции магнитного поля вдоль выбранной окружности равна:

[ointlimits_L<overrightarrowdoverrightarrow>=B2pi r left(1.1right).]

Тогда теорема о циркуляции предстанет в виде:

где $N$ — число витков с током. Выразим модуль вектора индукции, получим:

Задание: Какова циркуляция вектора индукции вдоль контура, который охватывает токи $I_1=5 A, I_2=6 A$, $I_3=10 A$, если первые два тока текут в одном направлении, третий в противоположном.

По теореме о циркуляции:

Для нашего случая имеем:

Проведем вычисление, получим:

[ointlimits_L<overrightarrowdoverrightarrow>=5+6-10=1 left(Тлcdot мright).]

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 09 02 2021

Видео:Электродинамика | теорема о циркуляции магнитной индукции | 1Скачать

Магнитное поле

155. Определите, во сколько раз постоянная Холла у меди больше, чем у алюминия, если известно, что в алюминии на один атом в среднем приходится два свободных электрона, а в меди – 0,8 свободных электронов. Плотность меди и алюминия соответственно равны 8,93 и 2,7 г/см 3 .

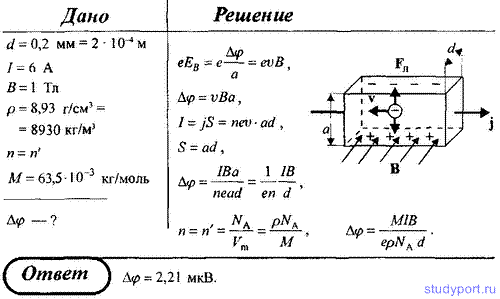
156. Через сечение пластинки толщиной d = 0,2 мм пропускается ток I = 6 А. Пластинка помещается в однородное магнитное поле индукцией В = 1 Тл, перпендикулярное ребру пластинки и направлению тока. Считая концентрацию электронов проводимости равной концентрации атомов, определить возникающую в пластинке поперечную (холловскую) разность потенциалов. Плотность меди ρ = 8,93 г/см 3 .

157. Определите циркуляцию вектора магнитной индукции по окружности, через центр которой перпендикулярно ее плоскости прохо бесконечно длинный прямолинейный провод, по которому течет ток I = 5 А.

158. Определите циркуляцию вектора магнитной индукции для замкнутых контуров, изобра на рисунке, если сила тока в обоих проводниках I = 2 А.

159. По прямому бесконечно длинному проводнику течет ток I = 10 А. Определите, пользуясь теоремой о циркуляции вектора В, магнитную индукцию В в точке, расположенной на расстоянии r = 10 см от проводника.

161. Соленоид длиной l = 0,5 м содержит N = 1000 витков. Определите магнитную индукцию В поля внутри соленоида, если сопротивление его обмоток R = 120 Ом, а напряжение на её концах U = 60 В.

162. В соленоиде длиной l = 0,4 м и диаметром D = 5 см создается магнитное поле, напряженность которого Н = 1,5 кА/м. Определите: 1) магнитодвижущую силу Fm; 2) разность потенциалов U на концах обмотки, если для нее используется алюминиевая проволока (ρ = 26 нОм*м) диаметром d = 1 мм.

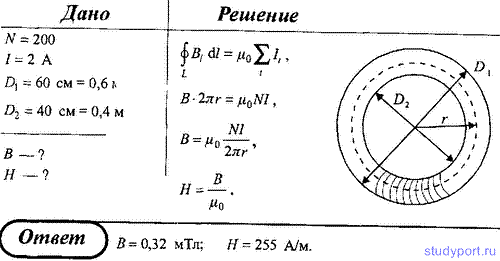
163. Определите, пользуясь теоремой о циркуляции вектора В, индукцию и напряженность магнитного поля на оси тороида без сердечника, по обмотке которого, содержащей 200 витков, протекает ток 2 А. Внешний диаметр тороида равен 60 см, внутренний – 40 см.

164. Определите магнитный поток сквозь площадь поперечного сечения катушки (без сердечника), имеющей на каждом сантиметре длины n = 8 витков. Радиус соленоида r = 2 см, сила тока в нем I = 2 А.

165. Внутри соленоида с числом витков N = 200 с никелевым сердечником (μ = 200) напряженность однородного магнитного поля Н = 10 кА/м. Площадь поперечного сечения сердечника S = 10 см 2 . Определите: 1) магнитную индукцию поля внутри соленоида; 2) потокосцепление.

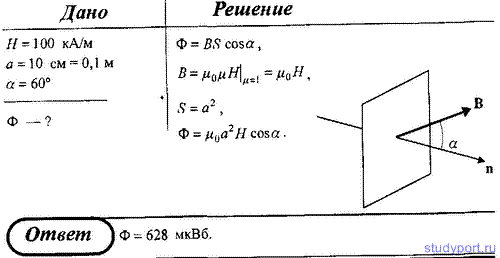
166. В однородное магнитное поле напряженность H = 100 кА/м помещена квадратная рамка со стороной a = 10 см. Плоскость рамки составляет с направлением магнитного поля угол α = 60°. Определите магнитный поток, пронизывающий рамку.

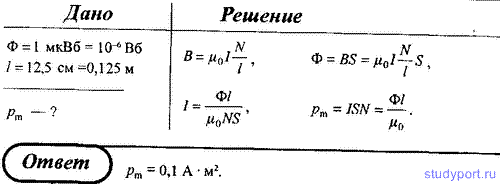
167. Поток магнитной индукции через площадь поперечного сечения соленоида (без сердечника) равен Ф = 1 мкВб. Длина соленоида l = 12,5 см. Определите магнитный момент р_m этого соленоида.

168. В одной плоскости с бесконечными прямолинейным проводом с током I = 20 А расположена квадратная рамка со стороной, длина которой a = 10 см, причем две стороны рамки параллельны проводу, а расстояние d от провода до ближайшей стороны рамки равно 5 см. Определите магнитный поток Ф, пронизывающий рамку.

169. Прямой провод длиной l = 20 см с током I = 5 А, находящийся в однородном магнитном поле с индукцией В = 0,1 Тл, расположен перпендикулярно линиям магнитной индукции. Определите работу сил поля, под действием которых проводник переместился на 2 см.

170. Квадратный проводящий контур со стороной l = 20 см и током I = 10 А свободно подвешен в однородном магнитном поле с магнитной индукцией В = 0,2 Тл. Определите работу, которую необходимо совершить, чтобы повернуть контур на 180° вокруг оси, перпендикулярной направлению магнитного поля.

171. В однородном магнитном поле с магнитной индукцией B = 0,2 Тл находится квадратный проводящий контур со стороной l = 20 см и током I = 10 А. Плоскость квадрата составляет с направлением поля угол в 30°. Определите работу удаления контура за пределы поля.

172. Круговой проводящий контур радиусом r = 5 см и током I = 1 А находится в магнитном поле, причем плоскость контура перпендикулярна направлению поля. Напряженность поля равна 10 кА/м. Определите работу, которую необходимо совершить, чтобы повернуть контур на 90° вокруг оси, совпадающей с диаметром контура.

173. В однородном магнитном поле с магнитной индукцией В = 1 Тл находится плоская катушка из 100 витков радиусом r = 10 см, плоскость которой с направлением поля составляет угол β = 60°. По катушке течет ток I = 10 А. Определите: 1) вращающий момент, действующий на ка; 2) работу для удаления этой катушки из магнитного поля.

174. Круглая рамка с током (S = 15 см 2 ) закреплена параллельно магнитному полю (В = 0,1 Тл), и на нее действует вращающий момент М = 0,45 мН * м. Определите силу тока, текущего по рамке.