С помощю этого онлайн калькулятора можно найти точку пересечения прямой и плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямой и плоскости задайте вид уравнения прямой («канонический» или «параметрический» ), введите данные в уравнения прямой и плоскости и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
- Предупреждение
- Точка пересечения прямой и плоскости − теория, примеры и решения
- 1. Точка пересечения плоскости и прямой, заданной в каноническом виде
- 2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
- 3. Примеры нахождения точки пересечения прямой и плоскости.
- Построение точки пересечения прямой и плоскости
- Видимость прямой a относительно плоскости α. Метод конкурирующих точек
- Пересечение прямой с плоскостью
- 🔍 Видео
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Точка встречи прямой с плоскостьюСкачать

Точка пересечения прямой и плоскости − теория, примеры и решения
- Содержание
- 1. Точка пересечения плоскости и прямой, заданной в каноническом виде.
- 2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
- 3. Примеры нахождения точки пересечения прямой и плоскости.
1. Точка пересечения плоскости и прямой, заданной в каноническом виде
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямая L1:
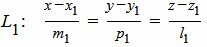 , , | (1) |
| α: Ax+By+Cz+D=0. | (2) |
Найти точку пересечения прямой L1 и плоскости α (Рис.1).
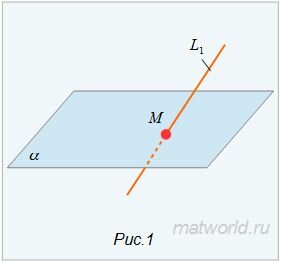 |
Запишем уравнение (1) в виде системы двух линейных уравнений:
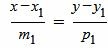 , , | (3) |
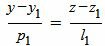 | (4) |
Сделаем перекрестное умножение в уравнениях (3) и (4):
| p1(x−x1)=m1(y−y1) |
| l1(y−y1)=p1(z−z1) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p1x−m1y=p1x1−m1y1, | (5) |
| l1y−p1z=l1y1−p1z1. | (6) |
Решим систему линейных уравнений (2), (5), (6) с тремя неизвестными x, y, z. Для этого в уравнении (2) переведем свободный член в правую часть уравнения и запишем эту систему в матричном виде:
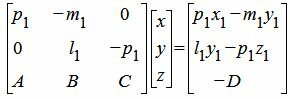 | (7) |
Как решить систему линейных уравнений (11)(или (2), (5), (6)) посмотрите на странице Метод Гаусса онлайн или на примерах ниже. Если система линейных уравнениий (7) несовместна, то прямая L1 и плоскость α не пересекаются. Если система (7) имеет множество решений, то прямая L1 лежит на плоскости α. Единственное решение системы линейных уравнений (7) указывает на то, что это решение определяет координаты точки пересечения прямой L1 и плоскости α.
Замечание. Если прямая задана параметрическим уравнением, то уранение прямой нужно приводить к каноническому виду и применить метод, описанный выше, или же
2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L1 в параметрическом виде:
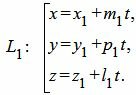 | (8) |
| α: Ax+By+Cz+D=0. | (9) |
Задачу нахождения нахождения точки пересечения прямых L1 и плоскости α можно решить разными методами.
Метод 1. Приведем уравнения прямой L1 к каноническому виду.
Для приведения уравнения (8) к каноническому виду, выразим параметр t через остальные переменные:
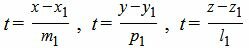 | (10) |
Так как левые части уравнений (10) равны, то можем записать:
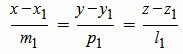 | (11) |
Далее, для нахождения точки пересечения прямой и плоскости нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямой L1 и плоскости α решим совместно уравнения (8) и (9). Из уравнений (8) подставим x, y, z в (9):
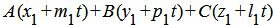 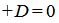 | (13) |
Откроем скобки и найдем t:
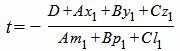 | (14) |
Если числитель и знаменатель в уравнении (14) одновременно равны нулю, то это значит, что прямая L1 лежит на полскости α. Если в уравнении (14) числитель отличен от нуля, а знаменатель равен нулю, то прямая и плоскость параллельны.
Если же числитель и знаменатель в уравнении (14) отличны от нуля, то прямая и плоскость пересекаются в одной точке. Для нахождения координат точки пересечения прямой L1 и плоскости α подставим полученное значение t из (14) в (8).
3. Примеры нахождения точки пересечения прямой и плоскости.
Пример 1. Найти точку пересечения прямой L1:
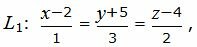 | (15) |
| α: 7x−5y+2z+19=0. | (16) |
Представим уравнение (15) в виде двух уравнений:
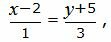 | (17) |
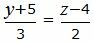 | (18) |
Сделаем перекрестное умножение в уравнениях (17) и (18):
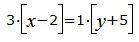 |
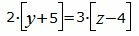 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
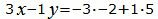 |
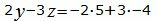 |
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (19) и (20). Для этого переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (19) и (20):
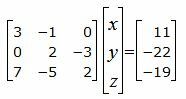 | (21) |
Решим систему линейных уравнений (21) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
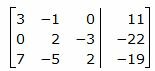 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −7/3:
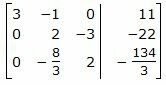 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на 4/3:
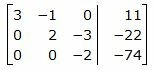 |
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −3/2:
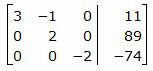 |
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 1/2:
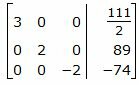 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
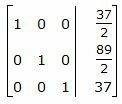 |
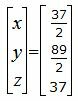 |
Ответ. Точка пересечения прямой L1 и плоскости α имеет следующие координаты:
| M (37/2, 89/2, 37). |
Пример 2. Найти точку пересечения прямой L1:
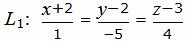 | (22) |
| α: 6x+2y+z+7=0. | (23) |
Представим уравнение (22) в виде двух уравнений:
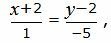 | (24) |
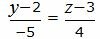 | (25) |
Сделаем перекрестное умножение в уравнениях (24) и (25):
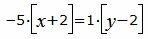 |
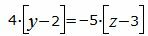 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
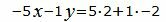 |
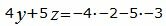 |
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (26) и (27). Переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (26) и (27):
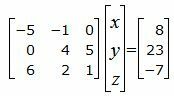 | (28) |
Решим систему линейных уравнений (21) отностительно x, y, z. Для этого построим расширенную матрицу:
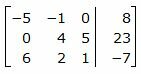 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 3 со строкой 1, умноженной на 6/5:
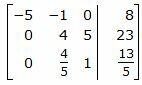 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на −1/5:
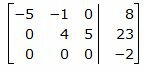 |
Из расширенной матрицы восстановим систему линейных уравнений:
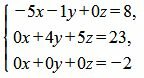 | (29) |
Легко можно заметить, что последнее уравнение в (29) несовместна, так как несуществуют такие x, y, z чтобы выполнялось это равенство. Следовательно система линейных уравнений (2), (26) и (27) несовместна. Тогда прямая L1 и плоскость α не пересекаются, т.е. они параллельны.
Ответ. Прямая L1 и плоскость α параллельны, т.е. не имеют общую точку.
Пример 3. Найти точку пересечения прямой в параметрическом виде L1:
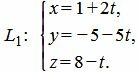 | (30) |
| α: 2x+y−z+11=0. | (31) |
Решение. Для нахождения точки пересечения прямой L1 и плоскости α нужно найти такое значение t, при котором точка M(x, y, z) удовлетворяет уравнению (31). Поэтому подставим значения x, y, z из (30) в (31):
| 2(1+2t)+(−5−5t)−(8−t)+11=0. |
| 2+4t−5−5t−8+t+11=0. | (32) |
Упростив уравнение, получим:
Как видим, любое значение t удовлетворяет уравнению (33), т.е. любая точка на прямой L1 удовлетворяет уравнению плоскости α. Следовательно прямая L1 лежит на плоскости α.
Ответ. Прямая L1 лежит на плоскости α.
Видео:Пересечение прямой с плоскостью общего положения. Определение видимости методом конкурирующих точекСкачать
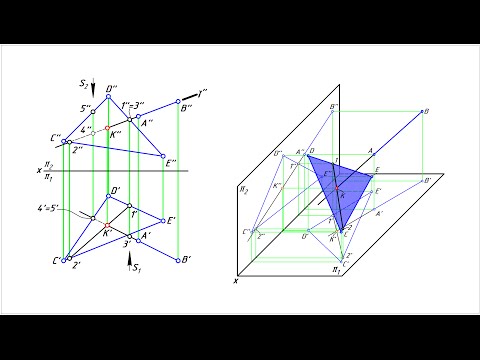
Построение точки пересечения прямой и плоскости
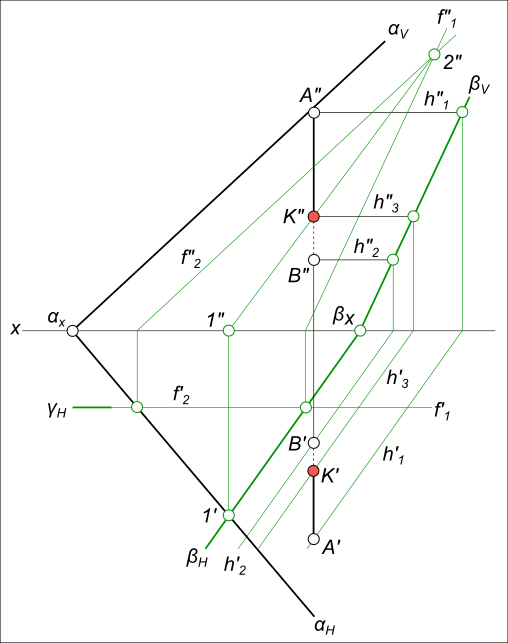
Известно, что прямая пересекает плоскость, если она не принадлежит этой плоскости и не параллельна ей. Следуя приведенному ниже алгоритму, найдем точку пересечения прямой a с плоскостью общего положения α, заданной следами h0α, f0α.
- Через прямую a проводим вспомогательную фронтально-проецирующую плоскость γ. На рисунке обозначены её следы h0γ, f0γ.
- Строим проекции прямой AB, по которой пересекаются плоскости α и γ. В данной задаче точка B’ = h0α ∩ h0γ, A» = f0α ∩ f0γ. Точки A’ и B» лежат на оси x, их положение определяется по линиям связи.
- Прямые a и AB пересекаются в искомой точке K. Её горизонтальная проекция K’ = a’ ∩ A’B’. Фронтальная проекция K» лежит на прямой a».
Алгоритм решения останется тем же, если пл. α будет задана параллельными, скрещивающимися прямыми, отсеком фигуры или другими возможными способами.
Видео:Параллельность прямой к плоскостиСкачать

Видимость прямой a относительно плоскости α. Метод конкурирующих точек
- Отметим на чертеже фронтально-конкурирующие точки A и С (рис. ниже). Будем считать, что точка A принадлежит пл. α, а С лежит на прямой a. Фронтальные проекции A» и С» совпадают, но при этом т. A и С удалены от плоскости проекций П2 на разное расстояние.
- Найдем горизонтальные проекции A’ и C’. Как видно на рисунке, точка C’ удалена от плоскости П2 на большее расстояние, чем т. A’, принадлежащая пл. α. Следовательно, участок прямой а», расположенный левее точки K», будет видимым. Участок a» правее K» является невидимым. Отмечаем его штриховой линией.
- Отметим на чертеже горизонтально-конкурирующие точки D и E. Будем считать, что точка D принадлежит пл. α, а E лежит на прямой a. Горизонтальные проекции D’ и E’ совпадают, но при этом т. D и E удалены от плоскости П1 на разное расстояние.
- Определим положение фронтальных проекций D» и E». Как видно на рисунке, точка D», находящаяся в пл. α, удалена от плоскости П1 на большее расстояние, чем т. E», принадлежащая прямой a. Следовательно, участок а’, расположенный правее точки K’, будет невидимым. Отмечаем его штриховой линией. Участок a’ левее K’ является видимым.
Видео:Построение точки пересечения прямой с плоскостью, заданной следамиСкачать
Пересечение прямой с плоскостью
Задача на пересечение прямой с плоскостью — это одна из основных задач, с ее применением сталкиваются при рассмотрении сечения тел плоскостями и пересечения поверхностей.
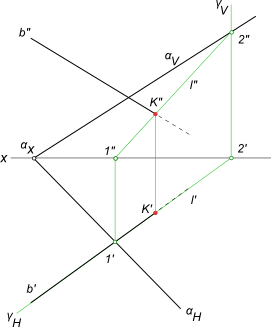
Нахождение точки встречи прямой с плоскостью, заданной пересекающимися прямыми
Плоскость и пересекающая ее прямая занимают общее положение.
(γ ∩ α) = l — прямая, пересекающаяся с прямой b.
На пересечение прямой с плоскостью составляем алгоритм нахождения их точки встречи :
1) проводим через b` горизонтальный след γH — горизонтально-проецирующей плоскости γ;
2) определяем фронтальную проекцию линии пересечения l, вспомогательной секущей плоскости γ с данной плоскостью α, используя для этого точки 1` и 2` (принадлежащие данной прямой), в которых горизонтальный след γH пересекает прямые c` и d`;
3) определяем точку K»=l»∩b». Зная K», находим K` на пересечении b` с линией проекционной связи.
Нахождение точки встречи прямой с плоскостью, заданной параллельными прямыми
Задача по нахождению точки встречи прямой с плоскостью заданной следами.
Алгоритм решения не меняется, если плоскость будет задана параллельными прямыми или прямыми, по которым она пересекает плоскости проекций (следы плоскости).
При решении задач на пересечение прямой с плоскостью в качестве вспомогательных плоскостей применяют проецирующие плоскости. Но в случае, например, профильной прямой они бесполезны и тогда надо применить плоскость общего положения.
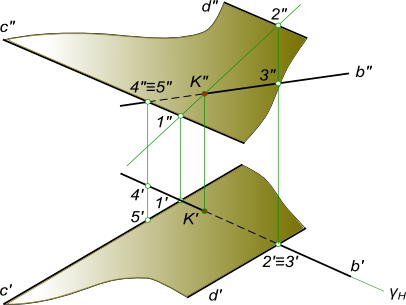
Найти точку встречи профильной прямой AB с плоскостью α заданной следами
Алгоритм выполнения геометрических построений: 1) Заключаем отрезок AB во вспомогательную секущую плоскость общего положения β; 2) Определяем проекции линии пересечения 1-2, вспомогательной секущей плоскости β с данной плоскостью α; 3) Определяем проекцию K» точки K на пересечении 1″-2″ с прямой A»B». Проекция K` точки K может быть найдена: — на пересечении A`B` с 1`-2`; — или как принадлежащая плоскостям α и β.
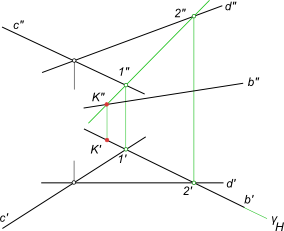
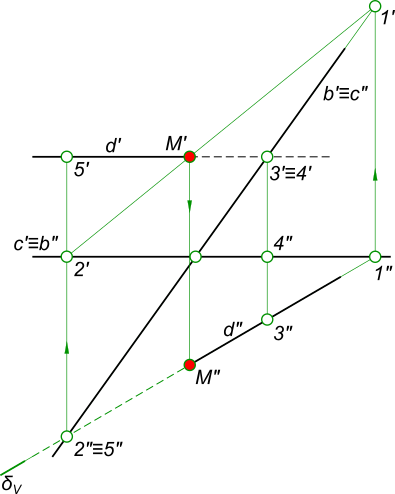
Найти точку встречи прямой d с плоскостью α(b, c), определить видимость
Алгоритм выполнения геометрических построений: 1) Заключаем прямую d во вспомогательную секущую фронтально проецирующую плоскость δ; 2) Определяем проекции линии пересечения 1-2, вспомогательной секущей плоскости δ с данной плоскостью α; 3) Определяем проекцию K` точки K на пересечении 1`-2` с прямой d`. Проекцию K» точки K находим в пересечении d» с линией проекционной связи.
Данный способ решения задачи — найти точку встречи профильной прямой с плоскостью заданной следами применен в статье: Сечение пирамиды плоскостью
Определение видимости пересечения прямой с плоскостью на плоскостях проекций выполняем, используя Конкурирующие точки 2, 3 и 4, 5.
🔍 Видео
Пересечение прямой и плоскостиСкачать

Пересечение прямой и плоскостиСкачать

Пересечение прямой линии с плоскостью Определение видимости прямойСкачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Задача №3 Определение точки пересечения прямой с плоскостьюСкачать

Лекция 2. Основная задача начертательной геометрии. Точка пересечения прямой с плоскостью.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

23. Точка пересечения прямой и плоскости / Проекция точки на плоскость / Проекция точки на прямуюСкачать

Найти точку пересечения прямой и плоскостиСкачать

Определение кратчайшей расстоянии от точки до плоскостиСкачать

Пересечение прямой и плоскости Определение видимости прямойСкачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

Построение точки пересечения прямой и плоскости | Стереометрия #29 | ИнфоурокСкачать

Линия пересечения плоскостейСкачать

Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать