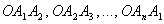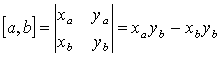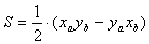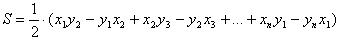Определить площадь выпуклого четырехугольника по заданным координатам вершин используя подпрограмму

Информатика | 10 — 11 классы

Задачу решить двумя способами : с использованием подпрограммы — функции и подпрограммы — процедуры.

Обязательно построение блок — схем алгоритмов!

1. Треугольник задан координатами своих вершин.

Вычислить площадь треугольника по формуле Герона с использованием подпрограммы нахождения расстояния между двумя точками на координатной плоскости.

Формула Герона : S = sqrt((p — a)(p — b)(p — c)) , где p = a + b + c / 2 (полупериметр треугольника со сторонами a, b и c)

Расстояние между двумя точками на координатной плоскости : d = sqrt(sqr(x2 — x1) + sqr(y2 — y1)) , где (x1, y1) и (x2, y2) – координаты первой и второй точек соответственно.

function Dlina(x1, y1, x2, y2 : integer) : real ;

d : = sqrt(sqr(y1 — y2) + sqr(x1 — x2)) ;

var xa, ya, xb, yb, xc, yc : integer ;

ab, bc, ca, S, p : real ;

writeln (‘введите коорд.

writeln (‘введите коорд.

writeln (‘введите коорд.

ab : = Dlina(xa, ya, xb, yb) ;

bc : = Dlina(xb, yb, xc, yc) ;

ca : = Dlina(xc, yc, xa, ya) ;

p : = (ab + bc + ca) / 2 ;

S : = sqrt(p * (p — ab) * (p — bc) * (p — ca)) ;

var x1, x2, x3, y1, y2, y3, s, a, b, c, p : real ;

procedure dlina(q, w, e, r : real ; var d : real) ;

d : = sqrt(sqr(q — w) + sqr(e — r)) ;

writeln (‘введите коорд.

writeln (‘введите коорд.

writeln (‘введите коорд.

dlina(x1, x2, y1, y2, a) ;

dlina(x2, x3, y2, y3, b) ;

dlina(x3, x1, y3, y1, c) ;

s : = sqrt(p * (p — a) * (p — b) * (p — c)) ;

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Построить блок схему алгоритма вычисления площади треугольника по формуле герона где р полупериметр треугольника со стронами а?

Построить блок схему алгоритма вычисления площади треугольника по формуле герона где р полупериметр треугольника со стронами а.

Видео:ОГЭ Задание 24 Площадь выпуклого четырехугольника с перпендикулярными диагоналямиСкачать

Для решения задачи сделать вариант программы с реализацией указанной подпрограммы в виде функции или в виде процедуры?

Для решения задачи сделать вариант программы с реализацией указанной подпрограммы в виде функции или в виде процедуры.

Даны координаты трех точек определить между какими из пар точек самое большое расстояние используя подпрограмму вычисления длины отрезка между двумя точками.

Видео:ОГЭ Задание 24 Площадь выпуклого четырехугольникаСкачать

Написать программу на Pascal для вычисления площади треугольника по его координатам(стороны вычисляются как L1 = )Площадь по формуле Герона?

Написать программу на Pascal для вычисления площади треугольника по его координатам

(стороны вычисляются как L1 = )

Площадь по формуле Герона.

Пожалуйста помогите (сделайте screen если можно).

Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

Информатики?

Помогите, срочно надо!

ВОТ ЗАДАЧА : Пользователь вводит с клавиатуры 3 числа a, b, c , являющиеся сторонами треугольника.

Написать программу использующую подпрограмму функцию для вычисления площади треугольника по формуле Герона.

(В паскале) Напишите пожалуйста программу Формула Герона : S = p * (p — a)(p — b)(p — c) (все под корнем).

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Даны координаты трех вершин треугольника : (Х1, у1 ), (х2, у2) , (х3, у3) ?

Даны координаты трех вершин треугольника : (Х1, у1 ), (х2, у2) , (х3, у3) .

Найти его периметр и площадь, используя формулу для расстояния между двумя точками на плоскости .

Для нахождения площади треугольника со сторонами а, b, с использовать формулу Герона : S = (p * (p — a) * (p — b) * (p — c))12, где p = (a + b + c) / 2 — — полупериметр.

Видео:Геометрия Найдите площадь выпуклого четырехугольника диагонали которого равны 3√3 см и 4 см а уголСкачать

Помогите составить программу и блок — схему к задаче : вычисление площади треугольника по формуле Герона?

Помогите составить программу и блок — схему к задаче : вычисление площади треугольника по формуле Герона.

Видео:Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

3. Даны три целых числа?

3. Даны три целых числа.

Определить, сумма цифр которого из них больше.

Подсчет суммы цифр организовать через подрограмму.

4. Определить площадь выпуклого четырехугольника по заданным координатам вершин.

Использовать подпрограмму — функцию вычисления длины отрезка и подпрограмму — процедуру вычисления площади треугольника по формуле Герона.

Видео:№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Дано 2 треугольника?

Дано 2 треугольника.

Координаты вершин с клавиатуры В программе должно быть первая процедура, вторая функция.

В процедуре должно считать стороны треугольников(по формуле нахождение сторон через координаты), всё это должно быть выражено через одну переменную!

(не знаю в цикле это как то чтоб через одну переменную и по двум точкам находить все стороны треугольников) в функции периметры треугольников.

В программе сумму периметров.

Видео:№370. Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1, 2, 4, 5.Скачать

Написать программу о нахождение площади равнобедренного треугольника по формуле Герона?

Написать программу о нахождение площади равнобедренного треугольника по формуле Герона.

Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Задано три чичла abc?

Задано три чичла abc.

Если a, b, c — стороны треугольника, то найти его площадь (по формуле Герона).

Перед вами страница с вопросом Задачу решить двумя способами : с использованием подпрограммы — функции и подпрограммы — процедуры?, который относится к категории Информатика. Уровень сложности соответствует учебной программе для учащихся 10 — 11 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Int x, y, b = 0 ; cout>>»введите х» ; cin»введите y» ; cin»x = » + х + » n» ; cout>>»y = » + y ; Логика 100% верная, но само написание может быть с ошибкой. С + + давно был.

1 Кбайт — 1024 байта. 2 Мбайта — 2048 Кбайта.

Var x, y : real ; begin readln(x, y) ; if (x> = 0)and(y.

1. Переведем объем из Мб в байты : 3, 5 Мб * 1024 = 3584 Кб 3584 Кб * 1024 = 3 670 016 байт 2. Т. к. 1 символ весит 1 байт. 3 670 016.

2. 5 кБайта = 2500 байт 1 байт = 8 бит 2500 * 8 = 20000.

КОМПЬЮТЕР 1)к «О»»М» ⇒КОМ 2)слово «путь», надо убрать последнюю букву и заменить букву»У» на «ЬЮ»⇒ПЬЮТ 3)слово «сердце», надо убрать первую и три последних буквы⇒ЕР Составить можно ребус, например, к слову «передача» : нарисовать большую букву «А».

#include using namespace std ; int main()>a ; if(a%2 = = 0)cout.

1) сделать поделку леса например 2) нарисовать плакат с загрязненой землей и какой мы хотим видеть 3) сделать схему марсианского ядра.

А)513 = 201 1)513 : 16 = 32 (1 ) 2)32 : 16 = 2 ( 0 ) Ответ : 513 = 201(в₁₆ — ричной системе счисления) Б)600 1)600 : 16 = 37 ( 8 ) 2)37 : 16 = 2 ( 5 ) Ответ : 600 = 258 (в₁₆ — ричной системе счисления) В)2010 1)2010 : 16 = 125 ( 10 = А ) 2)125 : 16 =..

А)201 б)258 в)7 da Вроде бы получается так.

Видео:Задание 3 ЕГЭ по математике. Урок 11Скачать

Вычисление площади выпуклого многоугольника по координатам вершин на плоскости

Вычисление площади выпуклого многоугольника по координатам вершин. Выпуклый многоугольник строится по точкам с использованием алгоритма Джарвиса

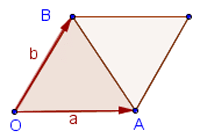
Калькулятор ниже был написан для решения частной задачи расчета площади выпуклого четырехугольника по координатам его вершин. Он только обобщает эту задачу до задачи расчета площади любого выпуклого многоугольника вообще. Собственно, на сайте уже был подобный калькулятор Площадь многоугольника, но там требовалось вводить длины сторон и диагоналей, а это несколько труднее, чем вводить только координаты вершин.

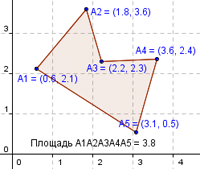
Принцип работы остается таким же — многоугольник разбивается на непересекающиеся треугольники, подсчитывается площадь всех треугольников (это легко сделать зная длины всех трех сторон — Расчет площади треугольника по формуле Герона), затем площади суммируются. Основная проблема была в том, чтобы сделать его устойчивым к ситуации, когда точки вводят не по порядку. Предположим, сначала вводят первые четыре точки получая фигуру на рисунке ниже

При добавлении следующей точки, например, так, как на следующем рисунке

должен уже получиться многоугольник ADCBE, а не ABCDE, разбитый на треугольники ADC, ACB и ABE, соответственно.

Чтобы получить правильный многоугольник, фактически требуется получить оболочку введенных точек. Для этого калькулятор использует алгоритм Джарвиса (или алгоритм обхода Джарвиса, или алгоритм заворачивания подарка), который определяет последовательность элементов множества, образующих выпуклую оболочку для этого множества. Метод можно представить как обтягивание верёвкой множества вбитых в доску гвоздей.

Алгоритм работает за время , где n — общее число точек на плоскости, h — число точек в выпуклой оболочке. Для выпуклого многоугольник соответственно будет . Не самый оптимальный алгоритм, зато очень простой, и для этого калькулятора вполне производительный.

Как пользоваться калькулятором: начинаете вводить координаты точек выпуклого многоугольника. Начиная с трех точек алгоритм Джарвиса будет стоить обтягивающий контур, затем контур будет разбиваться треугольники и подсчитываться общая площадь. Для справки также будут выводиться площади всех треугольников.

Видео:Как выпуклый четырёхугольник разрезать по прямой, содержащей его вершину, на две равновеликие части?Скачать

Урок 34. Площадь многоугольника

Урок из серии «Геометрические алгоритмы»

Здравствуйте, дорогой читатель.

Решения многих задач вычислительной геометрии основывается на нахождении площади многоугольника. На этом уроке мы выведем формулу для вычисления площади многоугольника через координаты его вершин, напишем функцию для вычисления этой площади.

Задача. Вычислить площадь многоугольника, заданного координатами своих вершин, в порядке их обхода по часовой стрелке.

Сведения из вычислительной геометрии

Для вывода формулы площади многоугольника нам понадобятся сведения из вычислительной геометрии, а именно, понятие ориентированной площади треугольника.

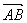
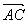
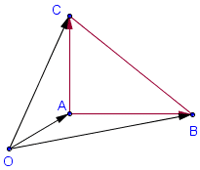
Ориентированная площадь треугольника – это обычная площадь, снабженная знаком. Знак ориентированной площади треугольника АВС такой же, как у ориентированного угла между векторами и . То есть ее знак зависит от порядка перечисления вершин.

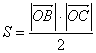
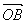
На рис. 1 треугольник АВС – прямоугольный. Его ориентированная площадь равна (она больше нуля, так как пара , ориентирована положительно). Эту же величину можно вычислить другим способом.

Пусть О – произвольная точка плоскости. На нашем рисунке площадь треугольника ABC получится, если из площади треугольника OBC вычесть площади OAB и OCA. Таким образом, нужно просто сложить ориентированные площади треугольников OAB, OBC и OCA. Это правило работает при любом выборе точки О.

Точно так же для вычисления площади любого многоугольника 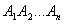нужно сложить ориентированные площади треугольников

В сумме получится площадь многоугольника, взятая со знаком плюс, если при обходе ломаной 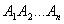многоугольника находится слева (обход границы против часовой стрелки), и со знаком минус, если он находится справа (обход по часовой стрелке).

Итак, вычисление площади многоугольника свелось к нахождению площади треугольника. Посмотрим, как выразить ее в координатах.

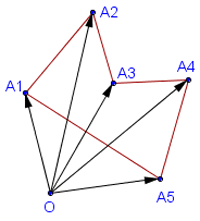
Векторное произведение двух векторов на плоскости есть площадь параллелограмма, построенного на этих векторах.

Векторное произведение, выраженное через координаты векторов:

Площадь треугольника будет равна половине этой площади:

В качестве точки О удобно взять начало координат, тогда координаты векторов, на основании которых вычисляются ориентированные площади, совпадут с координатами точек.

Пусть (х₁, y₁), (x₂, у₂), …, (х_N,у_N) —координаты вершин заданного многоугольника в порядке обхода по или против часовой стрелки. Тогда его ориентированная площадь S будет равна:

Это и есть наша рабочая формула, она используется в нашей программе.

Если координаты вершин были заданы в порядке обхода против часовой стрелки, то число S,вычисленное по этой формуле, получится положительным. В противном случае оно будет отрицательным, и для получения обычной геометрической площади нам необхо­димо взять его абсолютное значение.

Итак, рассмотрим программу для нахождения площади многоугольника, заданного координатами вершин.

Координаты вершин считывается из файла input.pas., хранятся в массиве А в виде записей с двумя полями. Для удобства обхода многоугольника в массиве вводится n+1 элемент, значение которого равно значению первого элемента массива.

Входные данные:
5
0.6 2.1 1.8 3.6 2.2 2.3 3.6 2.4 3.1 0.5

Выходные данные:
S= 3.91

Мы решили задачу о нахождении площади многоугольника по координатам его вершин. Задачи усложняются. Если у вас есть замечания к этой статье, или пожелания, напишите в комментарии. Буду Вам очень признательна за сотрудничество.

🌟 Видео

Диагонали четырехугольника равны 4 и 5.Скачать

Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

ОГЭ по математике. Площадь четырехугольника можно вычислить (вар. 4)Скачать

№366. Найдите стороны четырёхугольника, если его периметр равен 8 смСкачать

Найдите площадь четырёхугольникаСкачать

№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать

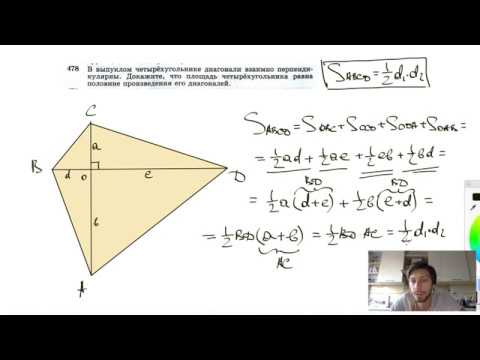
✓ Площадь через диагонали | Ботай со мной #122 | Борис ТрушинСкачать

Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать