Описанная окружность теорема замечания

Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема

Доказательство

Дано: произвольный АВС.

Доказать: около АВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.

Замечание 1

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Доказательство

Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Доказательство

Дано: четырехугольник АВСD, BАD + BСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)

Углы ВFD и FDE — вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.

BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .

Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 — ( В + F). (2)

В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)

F и ВFD — смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 — ВFD = 180 0 — ВАD. (4)

Подставим (3) и (4) в (2), получим:

С = 180 0 — (ЕF + 180 0 — ВАD) = 180 0 — ЕF — 180 0 + ВАD = (ВАD — ЕF), следовательно, СВАD.

А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.

Примечание:

Окружность всегда можно описать:

Поделись с друзьями в социальных сетях:

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Окружность, описанная около треугольника

Видео:8 класс, 39 урок, Описанная окружностьСкачать

Определение окружности, описанной около треугольника

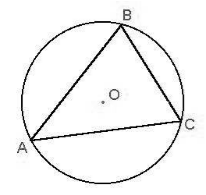
Определение 1. Окружностью, описанной около треугольника называется окружность, проходящей через все три вершины треугольника (Рис.1).

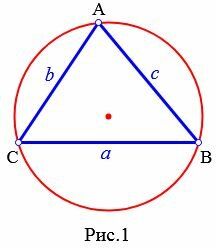При этом треугольник называется треугольником вписанным в окружность .

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Теорема об окружности, описанной около треугольника

Теорема 1. Около любого треугольника можно описать окружность.

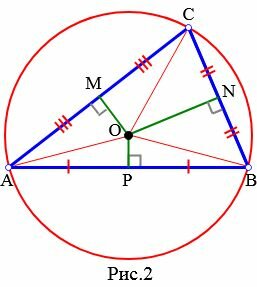Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения серединных перпендикуляров к его сторонам. Проведем отрезки OA, OB и OC. Поскольку точка O равноудалена от точек A, B и C, то OA=OB=OC. Тогда окружность с центром O и радиусом OA проходит через все три вершины треугольника ABC и, следовательно, является окружностью, описанной около треугольника ABC.

Из теоремы 1 следует, что центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника.

Замечание 1. Около любого треугольника можно описать только одну окружность.

Доказательство. Допустим, что около треугольника можно описать две окружности. Тогда центр каждой из этих окружностей равноудален от вершин треугольника и совпадает с точкой O пересечения серединных перпендикуляров сторон треугольника. Радиус этих окружностей равен расстоянию от точки O до вершин треугольника. Поэтому эти окружности совпадают.

Видео:110. Окружность, описанная около правильного многоугольникаСкачать

Вписанная и описанная окружности

Вы будете перенаправлены на Автор24

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Вписанная окружность

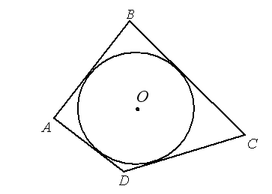
Если все стороны многоугольника являются касательными одной окружности, то такая окружность называется вписанной в многоугольник (рис 1).

Многоугольник, удовлетворяющий условию определения 1, называется описанным около окружности.

Рисунок 1. Вписанная окружность

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Теорема 1 (об окружности, вписанной в треугольник)

В любой треугольник можно вписать окружность и притом только одну.

Доказательство.

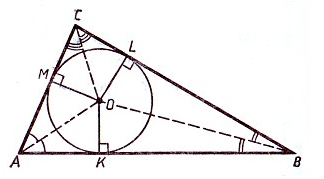
Рассмотрим треугольник $ABC$. Проведем в нем биссектрисы, которые пересекаются в точке $O$ и проведем из нее перпендикуляры на стороны треугольника (Рис. 2)

Рисунок 2. Иллюстрация теоремы 1

Существование: Проведем окружность с центром в точке $O$ и радиусом $OK. $Так как точка $O$ лежит на трех биссектрисах, то она равноудалена от сторон треугольника $ABC$. То есть $OM=OK=OL$. Следовательно, построенная окружность также проходит через точки $M и L$. Так как $OM,OK и OL$ — перпендикуляры к сторонам треугольника, то по теореме о касательной к окружности, построенная окружность касается всех трех сторон треугольника. Следовательно, в силу произвольности треугольника, в любой треугольник можно вписать окружность.

Готовые работы на аналогичную тему

Единственность: Предположим, что в треугольник $ABC$ можно вписать еще одну окружность с центром в точке $O’$. Её центр равноудален от сторон треугольника, а, следовательно, совпадает с точкой $O$ и имеет радиус, равный длине $OK$. Но тогда эта окружность совпадет с первой.

Теорема доказана.

Следствие 1: Центр вписанной в треугольник окружности лежит в точке пересечения его биссектрис.

Приведем еще несколько фактов, связанных с понятием вписанной окружности:

Не во всякий четырехугольник можно вписать окружность.

В любом описанном четырехугольнике суммы противоположных сторон равны.

Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Описанная окружность

Если на окружности лежат все вершины многоугольника, то окружность называется описанной около многоугольника (Рис. 3).

Многоугольник, удовлетворяющий условию определения 2, называется вписанным в окружность.

Рисунок 3. Описанная окружность

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Теорема 2 (об окружности, описанной около треугольника)

Около любого треугольника можно описать окружность и притом только одну.

Доказательство.

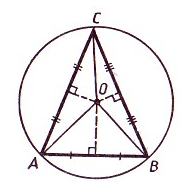
Рассмотрим треугольник $ABC$. Проведем в нем серединные перпендикуляры, пересекающиеся в точке $O$, и соединим ее с вершинами треугольника (рис. 4)

Рисунок 4. Иллюстрация теоремы 2

Существование: Построим окружность с центром в точке $O$ и радиусом $OC$. Точка $O$ равноудалена от вершин треугольника, то есть $OA=OB=OC$. Следовательно, построенная окружность проходит через все вершины данного треугольника, значит, она является описанной около этого треугольника.

Единственность: Предположим, что около треугольника $ABC$ можно описать еще одну окружность с центром в точке $O’$. Её центр равноудален от вершин треугольника, а, следовательно, совпадает с точкой $O$ и имеет радиус, равный длине $OC.$ Но тогда эта окружность совпадет с первой.

Теорема доказана.

Следствие 1: Центр описанной около треугольника окружности совпадает с точкой пересечения его серединных перпендикуляров.

Приведем еще несколько фактов, связанных с понятием описанной окружности:

Около четырехугольника не всегда можно описать окружность.

В любом вписанном четырехугольнике сумма противоположных углов равна $^0$.

Если сумма противоположных углов четырехугольника равна $^0$, то около него можно описать окружность.

Видео:Построить описанную окружность (Задача 1)Скачать

Пример задачи на понятия вписанной и описанной окружности

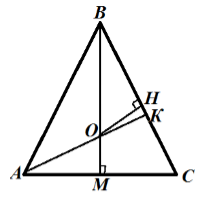
В равнобедренном треугольнике основание равно 8 см, боковая сторона равна 5 см. Найти радиус вписанной окружности.

Решение.

Рассмотрим треугольник $ABC$. По следствию 1, мы знаем, что центр вписанной окружности лежит на пересечении биссектрис. Проведем биссектрисы $AK$ и $BM$, которые пересекаются в точке $O$. Проведем перпендикуляр $OH$ из точки $O$ на сторону $BC$. Изобразим рисунок:

Так как треугольник равнобедренный, то $BM$ и медиана и высота. По теореме Пифагора $^2=^2-^2, BM=sqrt<^2-frac<^2>>=sqrt=sqrt=3$. $OM=OH=r$ — искомый радиус вписанной окружности. Так как $MC$ и $CH$ отрезки пересекающихся касательных, то по теореме о пересекающихся касательных, имеем $CH=MC=4 см$. Следовательно, $BH=5-4=1 см$. $BO=3-r$. Из треугольника $OHB$, по теореме Пифагора, получим:

Ответ: $frac$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 29 03 2022

🌟 Видео

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Описанная окружностьСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Описанная окружность | Геометрия 7-9 класс #75 | ИнфоурокСкачать

8 класс, 38 урок, Вписанная окружностьСкачать

Радиус описанной окружностиСкачать

Описанная и вписанная окружности треугольника - 7 класс геометрияСкачать

Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Теорема об описанной окружностиСкачать

Углы, вписанные в окружность. 9 класс.Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать