В немногие из многоугольников можно вписать окружность. Окружность будет называться вписанной в многоугольник, если она касается всех его сторон. При этом, поскольку каждая сторона является касательной к окружности, то из свойств последней следует, что она находится под прямым углом к радиусу вписанной окружности. Радиусы, проведенные к сторонам многоугольника из центра окружности, имеют первостепенное значение, так как они фигурируют во многих расчетах по данным фигурам, в том числе и без окружности, как таковой. Центр окружности, вписанной в многоугольник, можно найти, проведя две биссектрисы из любых углов, точка их пересечения и будет искомым центром. Для того чтобы различать в формулах радиусы вписанной и описанной окружностей их обозначают r и R соответственно длине.
Вокруг определенных геометрических фигур можно описать окружность. Если для каждой стороны провести срединный перпендикуляр, или медиатрису, то точка их пересечений (достаточно двух) будет центром описанной вокруг фигуры окружности. Такая окружность содержит все вершины углов многоугольника. Радиусы, соединяющие центр окружности с вершинами многоугольника, участвуют во многих вычислениях и решениях типовых задач на нахождение сторон, площадей и других параметров данных фигур. Радиусы описанных окружностей обозначаются R , а радиусы вписанных окружностей – r , для различия.
- Сколько малых одинаковых окружностей радиуса r можно вписать в большую окружность радиуса R
- Квадрат. Онлайн калькулятор
- Свойства квадрата
- Диагональ квадрата
- Окружность, вписанная в квадрат
- Формула вычисления радиуса вписанной окружности через сторону квадрата
- Формула вычисления сторон квадрата через радиус вписанной окружности
- Окружность, описанная около квадрата
- Формула радиуса окружности описанной вокруг квадрата
- Формула стороны квадрата через радиус описанной около квадрата окружности
- Периметр квадрата
- Признаки квадрата
- 📽️ Видео
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Сколько малых одинаковых окружностей радиуса r можно вписать в большую окружность радиуса R
Этот калькулятор оценивает число малых окружностей заданного радиуса r можно разместить внутри большой окружности заданного радиуса R.
Этот калькулятор выводит максимальное число малых окружностей заданного радиуса r можно разместить внутри большой окружности заданного радиуса R. Например это могут быть малые трубы внутри большой, провода в кабель канале, круги, вырезаемые из круговой же заготовки и так далее.
Вы можете подумать, что для решения такой задачи должна быть выведена формула, но на самом деле это не так — формулы нет. Эта задача относится к классу оптимизационных задач, а точнее, задач упаковки. Эта задача известна как Упаковка кругов в круге. Упаковка кругов в круге — это двумерная задача упаковки, целью которой является упаковка единичных кругов в как можно меньший круг. См. Упаковка кругов в круге.
Для этой задачи найденное решение еще и должно быть проанализировано на оптимальность. Статья в википедии по ссылке выше приводит первые 20 решений (иными словами, приводит минимальные радиусы больших окружностей вмещающих заданное число единичных окружностей. Между прочим, по умолчанию входные параметры калькулятора дают ответ 11 кругов, что соответствует следующей диаграмме:
Хорошей новостью является то, что есть проект в интернете, целиком посвященный задачам упаковки — сайт Packomania. На сегодняшний день он содержит все найденные решения, автор сайта, Экард Спехт (Eckard Specht), сам участвует в поиске решений, и большинство решений, на самом деле найдены им. Оттуда можно взять соотношения r к R для решений, позволяющих упаковать от 1 до 2600 окружностей внутри большой, с графическими диаграммами решения.
Соотношения r/R, приведенные на сайте и использует калькулятор ниже для поиска оптимального решения. Если соотношение не попадает в диапазон известных решений, калькулятор выдает ошибку.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Квадрат. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):
 |
Можно дать и другие определение квадрата.
Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Свойства квадрата
- Длины всех сторон квадрата равны.
- Все углы квадрата прямые.
- Диагонали квадрата равны.
- Диагонали пересекаются под прямым углом.
- Диагонали квадрата являются биссектрисами углов.
- Диагонали квадрата точкой пересечения делятся пополам.
Изложеннные свойства изображены на рисунках ниже:
      |
Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Диагональ квадрата
Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.
 |
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 |
 . . | (1) |
Из равенства (1) найдем d:
 . . | (2) |
Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.
Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:
 |
Ответ:
Видео:Углы, вписанные в окружность. 9 класс.Скачать

Окружность, вписанная в квадрат
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):
 |
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Формула вычисления радиуса вписанной окружности через сторону квадрата
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
 | (3) |
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
 |
Ответ:
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Формула вычисления сторон квадрата через радиус вписанной окружности
Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:
 | (4) |
Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.
Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:
 |
Ответ:
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Окружность, описанная около квадрата
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):
 |
Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Формула радиуса окружности описанной вокруг квадрата
Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.
Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:
 |
 | (5) |
Из формулы (5) найдем R:
 |
 | (6) |
или, умножая числитель и знаменатель на 
 . . | (7) |
Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.
Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:
 |
Ответ:
Видео:Построить описанную окружность (Задача 1)Скачать

Формула стороны квадрата через радиус описанной около квадрата окружности
Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.
Из формулы (1) выразим a через R:
 |
 . . | (8) |
Пример 5. Радиус описанной вокруг квадрата окружности равен 
Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя 
 |
Ответ:
Видео:Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Периметр квадрата
Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:
 | (9) |
где 
Пример 6. Сторона квадрата равен 
Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя 
 |
Ответ:
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.
Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
 |
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
 | (10) |
Так как AD и BC перпендикулярны, то
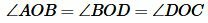 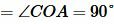 | (11) |
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
 | (12) |
Эти реугольники также равнобедренные. Тогда
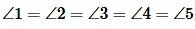 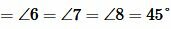 | (13) |
Из (13) следует, что
 | (14) |
Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
📽️ Видео
Как решать задания на окружность ОГЭ 2021? / Разбор всех видов окружностей на ОГЭ по математикеСкачать

8 класс, 38 урок, Вписанная окружностьСкачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Вписанные углы в окружностиСкачать

Окружность, диаметр, хорда геометрия 7 классСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Длина окружности. Математика 6 класс.Скачать

9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать







