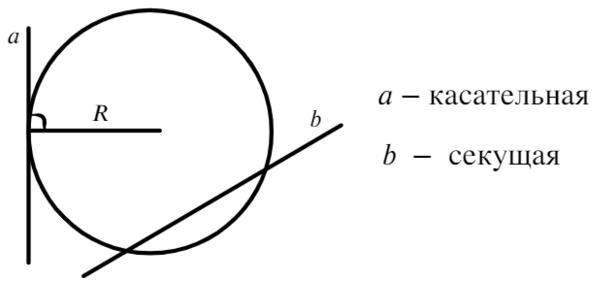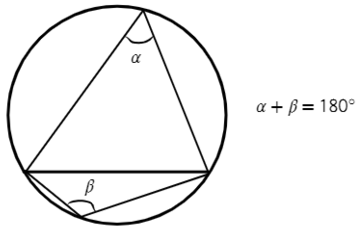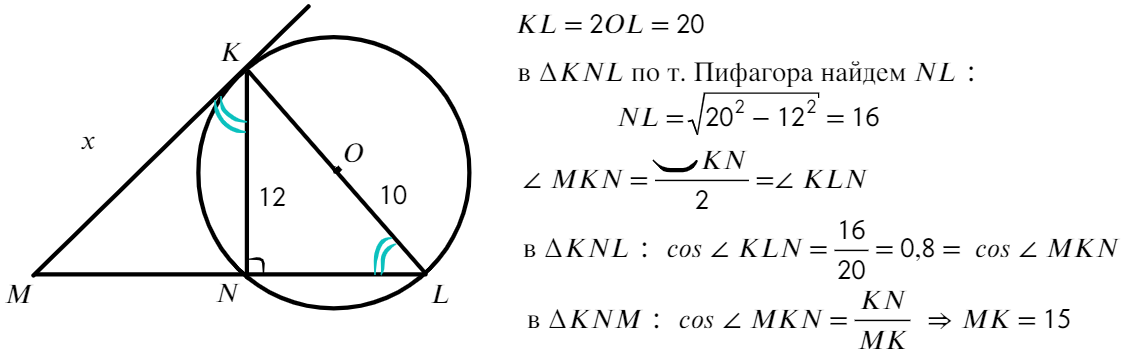Как найти величину дуги окружности зная вписанный угол

О чем эта статья:

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

• Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

• Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

• Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

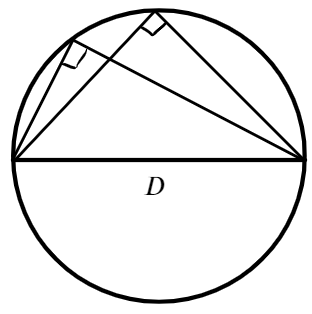
• Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

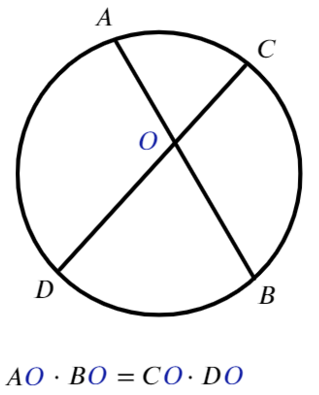
• Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

• Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

• Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

Теория и практика окружности

Свойство касательных.

Свойства касательных и секущих.

Площадь, сектор, длина окружности.

Задачи на окружности.

По статистике окружности никто не любит, но при этом леденец любим, солнце любим, давай и окружность полюбим!

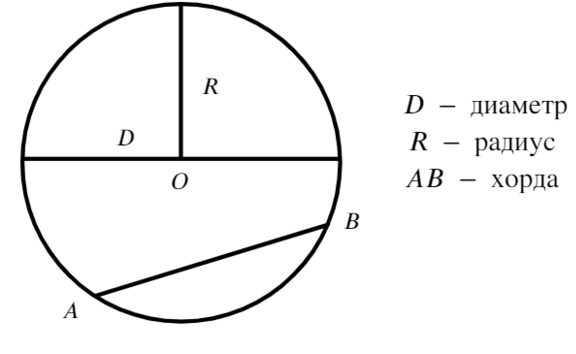
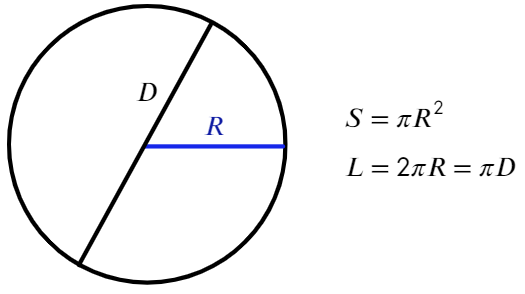
Окружность − геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). На рисунке центр − точка О.

В окружности может быть проведено 3 типа отрезка:

Отрезок, проходящий через две точки окружности, но не через центр, называют хордой (AB).

Хорда, проходящая через центр окружности, называется диаметром (самая большая хорда в окружности − диаметр (D)).

Радиус − отрезок, соединяющий центр окружности с точкой на окружности. Диаметр в два раза больше радиуса (R).

А также две прямые снаружи от окружности:

Касательная имеет одну общую точку с окружностью. Сразу стоит сказать о том, что радиус, проведенный в точку касания, будет иметь с касательной угол 90°.

Секущая пересекает окружность в двух точках, внутри окружности получается хорда или, в частном случае, диаметр.

Теперь чуть-чуть об углах и дугах:

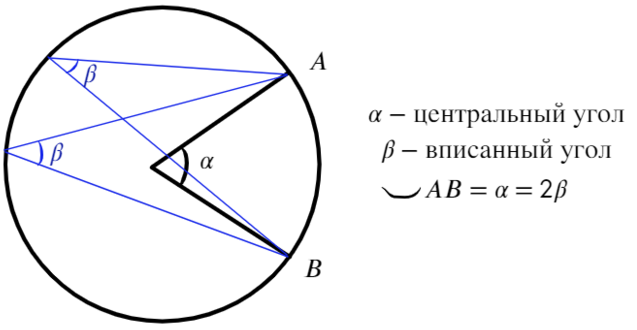
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее. Он в два раза меньше дуги, на которую опирается.

Центральный угол — это угол, вершина которого находится в центре окружности, равен дуге на которую опирается.

Вписанные углы, опирающиеся на одну дугу, равны между собой (β=β=α/2) и равны половине дуги, на которую опираются.

Градусная мера дуги – величина в °, соответствует центральному углу. Длина дуги равна α.

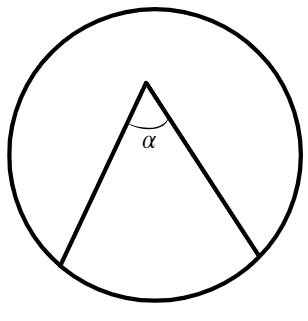
А вот такой угол НЕвписанный, такой угол «никто и звать никак».

Можно сделать вывод, что вписанный угол, который опирается на половину дуги окружности, будет прямым, а также будет опираться на диаметр:

Любая пара углов, опирающихся на одну и ту же хорду, вершина которых находится по разные стороны от хорды, составляет в сумме 180°.

Запишем основные свойства углов в окружности:

Нашел что-то общее?

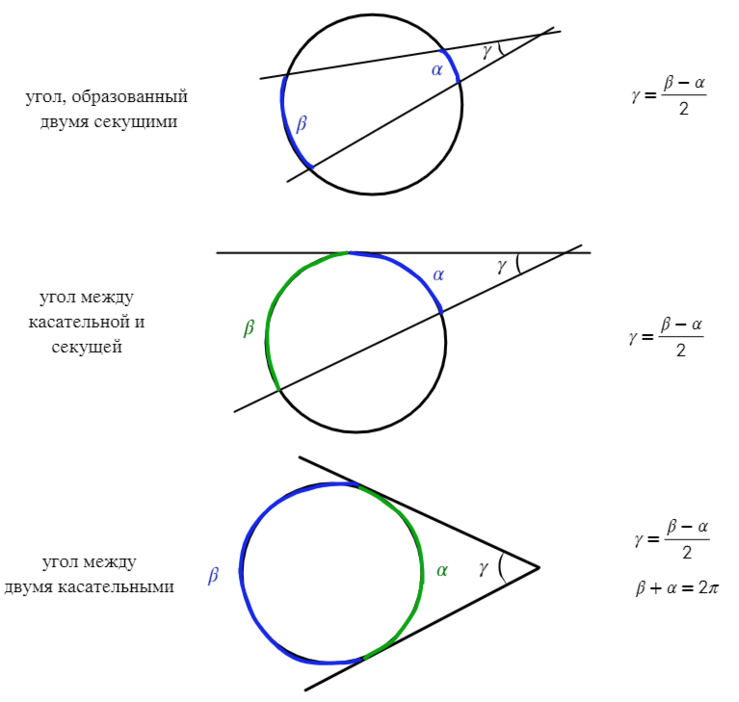
Если угол находится вне окружности, без разницы, чем он получен (касательной или секущей), то найти его можно через половину разности дуг.

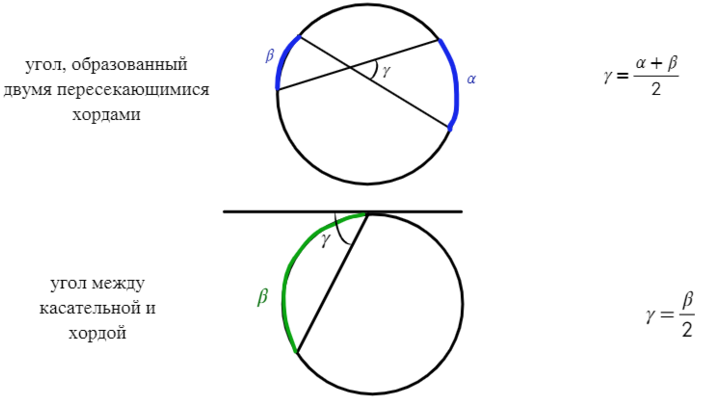
Если угол находится внутри окружности, то находим его через полусумму дуг.

Если есть одна дуга, которая находится на требуемом угле, то угол равен половине этой дуги.

Для любых двух хорд, проходящих через некоторую точку О, выполняет равенство:

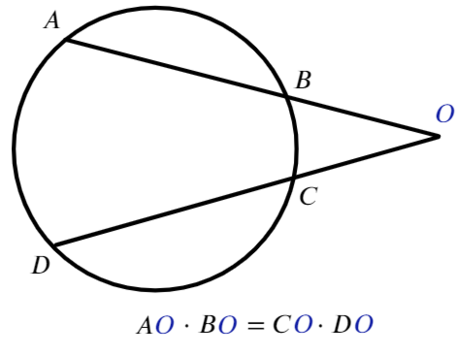
Для любых двух секущих, проходящих через некоторую точку O, выполняется равенство:

Согласен, что они похожи, особенно если не смотреть на картинки.
Как не перепутать такие равенства? В каждом отрезке должна присутствовать точка, вне окружности (О).

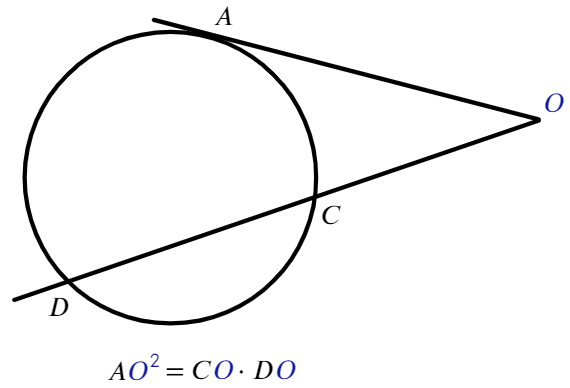
Если из точки, лежащей вне окружности, проведены касательная и секущая:

Аналогично в каждом отрезке присутствует точка, вне окружности (О).

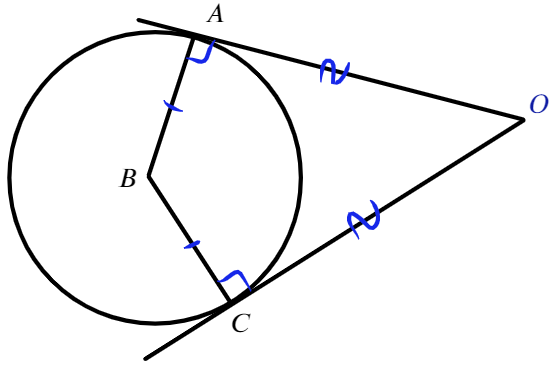
Если теперь провести две касательные из точки O, то получим такие равные отрезки:

Касательные равны, как, сообственно, и радиусы!

Площадь и длина окружности находятся по формуле:

По своему определению число π показывает, во сколько раз длина окружности больше диаметра, отсюда такая формула: L = πD

Если хочешь вывести площадь круга, можешь проинтегрировать длину окружности относительно R или вывести зависимость, как сделал Архимед!

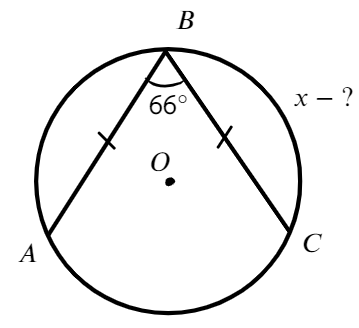
Задача №1. Дано на рисунке:

Достаточно вспомнить свойства центральных и вписанных углов.

Ответ: 39°

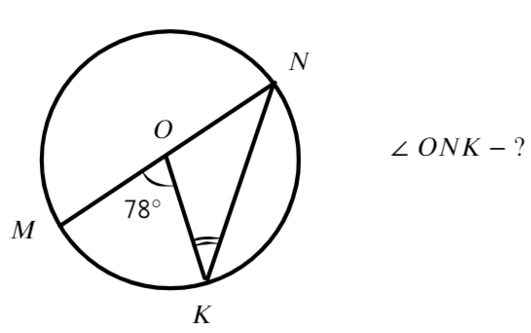
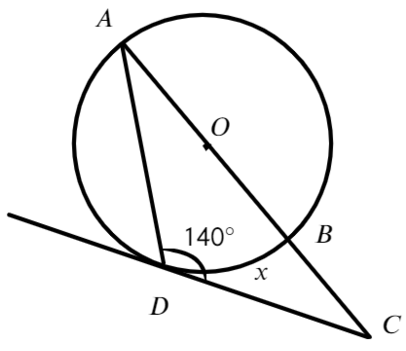
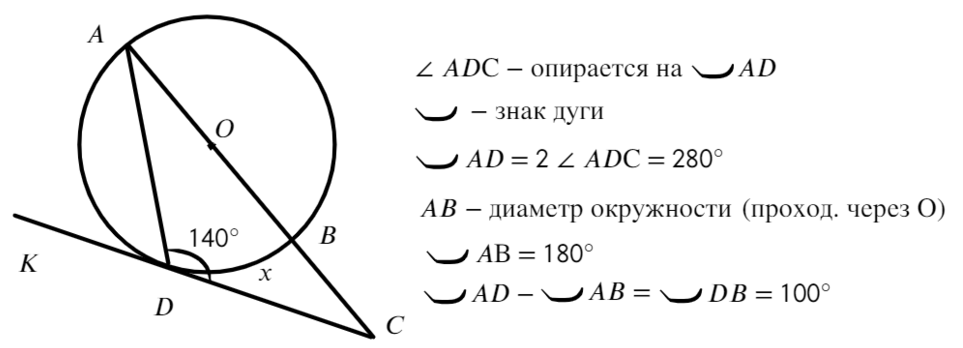
Задача №2. Дано на рисунке:

Найти нужно меньшую дугу BD

Ответ: 100°

Задача №3. Дано на рисунке:

Найти меньшую дугу ВС

Ответ: 114°

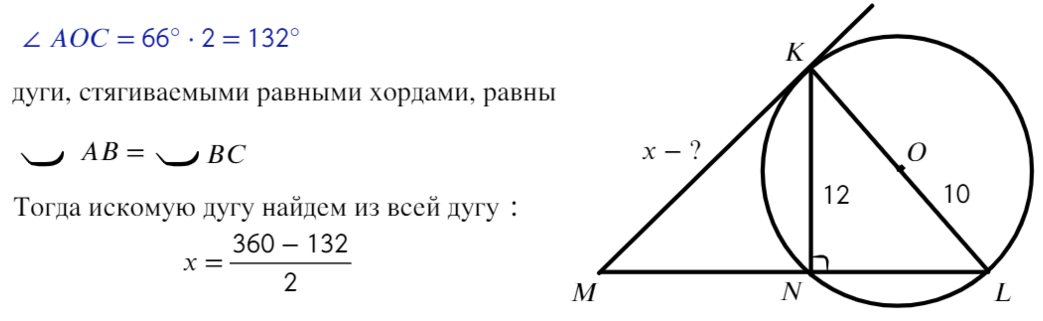
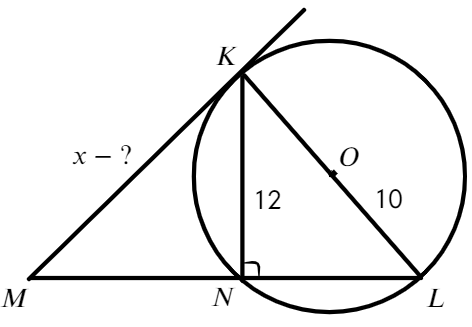
Задача №4. Дано на рисунке:

Найти отрезок МК

Ответ: МК = 15.

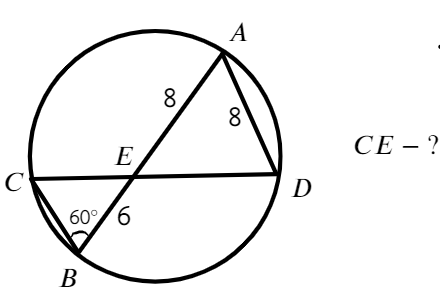
Задача №5. Дано на рисунке:

Попробуй найти подобные треугольники

Ответ: 6

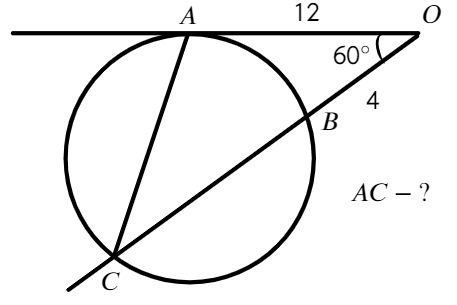
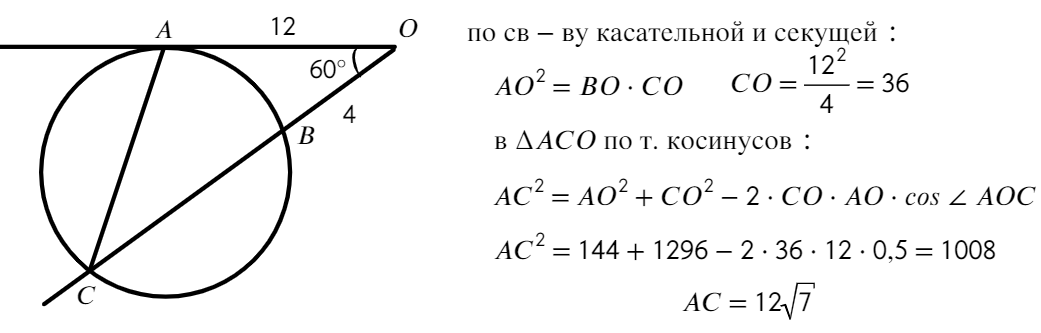
Задача №5. Дано на рисунке:

Без свойства секущей и касательной здесь будет тяжело

Ответ: 12√7.

Я могу долго тебе показывать, как решать задачи, но без твоих усилий ничего не выйдет.

О треугольниках
О четырехуголниках

p.s. Не бойся ошибаться и задавать вопросы!

Если нашел опечатку, или что-то непонятно − напиши.

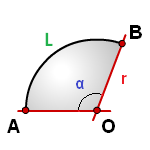
Как найти длину дуги окружности ?

r — радиус окружности

α — угол AOB, в градусах

Формула длины дуги ( L ):

Калькулятор для расчета длины дуги окружности :

Формулы для окружности и круга: