Условие
Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.
а) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей.
б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 3 и 2.
Решение
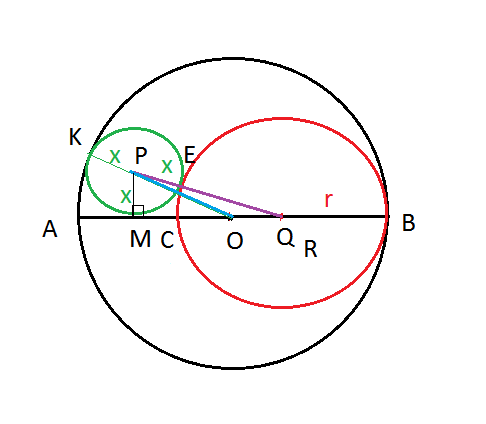
Обозначим центр большой окружности О, её радиус R. Центр окружности, касающейся большой окружности внутренним образом Q, радиус r,центр третьей окружности, касающейся этих двух Р, радиус х.
См. рисунок.
а)Рассмотрим треугольник POQ.
Прямая, соединяющая центры касающихся окружностей проходит через точку касания.
АВ- линия центров окружностей, касающихся внутренним образом, проходит через точки О и Q.
AB=2R; CD=2r ⇒ OQ=R-r.
РО=R-x
PQ=x+r.
Р(Δ PQO)=PQ+QO+PO=R-x+R-r+x+r=2R
б)Рассматриваем два прямоугольных треугольника.
МРО и МРQ.
М- точка касания третьей окружности с линией центров первых двух.
Значит РМ⊥АВ.
Находим МО по теореме Пифагора из Δ МРО:
МО^2=PO^2-PM^2=(R-x)^2-x^2 ⇒
МО= sqrt((R-x)^2-x^2)
Находим МО по теореме Пифагора из Δ МРО:
МQ^2=PQ^2-PM^2=(r+x)^2-x^2 ⇒
МQ= sqrt((r+x)^2-x^2)
Так как MQ=MO+OQ, приравнивая получаем иррациональное уравнение:
sqrt((r+x)^2-x^2)=sqrt((R-x)^2-x^2)+ (R-r).
При R=3; r=2
sqrt((2+x)^2-x^2)=sqrt((3-x)^2-x^2)+ 1.
Возводим в квадрат.
(2+x)^2-x^2=(3-x)^2-x^2+2sqrt((3-x)^2-x^2)+1;
2sqrt((3-x)^2-x^2)=10х-6;
sqrt((3-x)^2-x^2)=5х-3.
Возводим в квадрат.
(3-х)^2-x^2=25x^2-30x+9;
25x^2-24x=0
x=0,96 или х=0- не удовл. условию задачи
О т в е т. 0,96 
Окружности касаются внутренним образом третья окружность
2021-11-23 
Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.
а) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей.
б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 6 и 2.
а) Пусть $AB$ — диаметр большей из трёх окружностей (рис.1), $O$ — её центр, $O_$ — центр окружности радиуса $r$, касающейся окружности с диаметром $AB$ в точке $A$, $O_$ — центр окружности радиуса $R$, касающейся окружности с диаметром $AB$ в точке $C$, окружности с центром $O_$ — в точке $D$, отрезка $AB$ — в точке $E$.
Точки $O$, $O_$ и $C$ лежат на одной прямой, поэтому $OO_=OC-O_C=OC-R$. Аналогично $OO_=OA-O_A=OA-r$ и $O_O_=O_D+O_D=r+R$. Следовательно, периметр треугольника $OO_O_$ равен
б) Пусть $OA=6$, $r=2$. Тогда
Из прямоугольных треугольников $O_O_E$ и $OO_E$ находим, что
Если точка $E$ лежит на отрезке $OB$ (рис.2), то $O_E=OO_+OE$, или $sqrt=4+sqrt$. Из этого уравнения находим, что $R=3$ (это значит, что диаметр искомой окружности равен радиусу наибольшей из трёх окружностей, т.е. точка $E$ совпадает с $O$).
Если точка $E$ лежит на отрезке $OA$, то аналогично получим тот же результат.
Окружности касаются внутренним образом третья окружность
Задание С4 (Семенов, Ященко, Высоцкий, ЕГЭ по математике 2014)
Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.
а) Докажите, что периметр треугольника с вершинами в центрах трех окружностей равен диаметру наибольшей из этих окружностей.
б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 6 и 2.
Задание С4 (Семенов, Ященко, Высоцкий, ЕГЭ по математике 2012)
Дан ромб ABCD с диагоналями AC = 24 и BD = 10. Проведена окружность радиуса 
с центром в точке пересечения диагоналей ромба. Прямая, проходящая через вершину B, касается этой окружности и пересекает прямую CD в точке M. Найдите CM.
Ответ: 91/17 или 221/7.
Задание С4 (Семенов, Ященко, Высоцкий, ЕГЭ по математике 2012)
В треугольнике ABC AB = 7, BC = 9, CA = 4. Точка D лежит на прямой BC так, что BD:DC = 1:5. Окружности, вписанные в каждый из треугольников ADC и ADB, касаются стороны AD в точках E и F. Найдите длину отрезка EF.
Задание С4 (Семенов, Ященко, Высоцкий, ЕГЭ по математике 2012)
Основание равнобедренного треугольника равно 40, косинус угла при вершине равен 15/17. Две вершины прямоугольника лежат на основании треугольника, а две другие — на боковых сторонах. Найдите площадь прямоугольника, если известно, что одна из его сторон вдвое больше другой.
Ответ: 512 или 800.
Задание С4 (Семенов, Ященко, Высоцкий, ЕГЭ по математике 2012)
Высота равнобедренного треугольника, опущенная на основание, равна 9, а радиус вписанной в трегольник окружности, равен 4. Найдите радиус окружности, касающейся стороны треугольника и продолжений двух других его сторон.
Задание С4 (Семенов, Ященко, Высоцкий, ЕГЭ по математике 2012)
Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок этой прямой, заключенный внутри треугольника, равен 6, а отношение катетов треугольника равно 3/4.
Задание С4 (Семенов, Ященко, Высоцкий, ЕГЭ по математике 2012)
Окружность S проходит через вершину C прямого угла и пересекает его стороны в точках, удаленных от вершины C на расстояния 6 и 8. Найдите радиус окружности, вписанной в данный угол и касающейся окружности S.
Задание С4 (Семенов, Ященко, Высоцкий, ЕГЭ по математике 2014)
На стороне BA угла ABC, равного 
, взята такая точка D, что AD = 2 и BD = 1. Найдите радиус окружности, проходящей через точки A,D и касающейся прямой BC.
Задание С4 (Семенов, Ященко, Высоцкий, ЕГЭ по математике 2014)
В треугольнике ABC AB = 12, BC = 5, AC = 10. Точка D лежит на прямой BC так, что BD:DC = 4:9. Окружности, вписанные в каждый из треугольников ABD и ACD, касаются стороны AD в точках E и F. Найдите длину отрезка EF.
Ответ: 