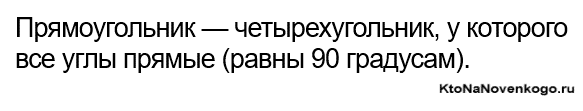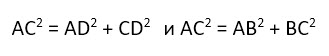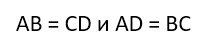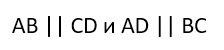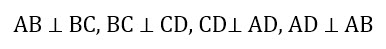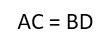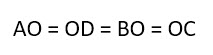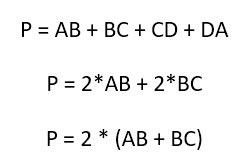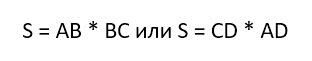- теория по математике 📈 планиметрия
- Выпуклый четырехугольник
- Виды и свойства выпуклых четырехугольников
- Прямоугольник
- Квадрат
- Параллелограмм
- Трапеция
- Виды трапеций
- Средняя линия трапеции
- Тест по геометрии «Четырехугольники»
- «Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
- Стопичева Вера Ивановна, учитель математики МОУ Иловская СОШ им. Героя России В. Бурцева
- Тест по теме «Четырехугольники» 8 класс
- Пояснительная записка к тесту по теме
- «Четырехугольники» 8 класс.
- Тест рассчитан на 5 — 10 минут, в зависимости от подготовленности обучающихся. Рекомендуется провести его после изучения темы «Четырехугольники». Так же можно выполнить задания теста при подготовке к ОГЭ по математике.
- Вариант 1.
- Вариант 2.
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Подарочные сертификаты
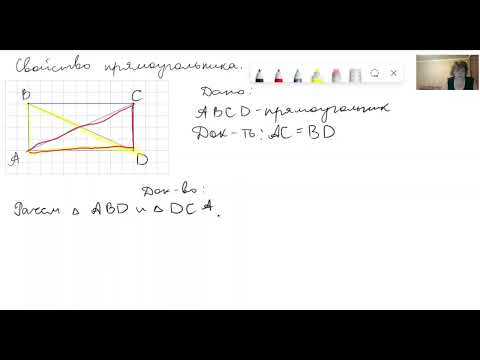
- Прямоугольник — это одна из основ геометрии
- Прямоугольник — это.
- Признаки прямоугольника
- Диагонали прямоугольника
- Свойства прямоугольника
- Периметр и площадь
- Комментарии и отзывы (5)
- 📺 Видео
теория по математике 📈 планиметрия
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
Выпуклый четырехугольник
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.
Видео:Геометрия Признак прямоугольника Доказательство. Если диагонали параллелограмма равны, то этотСкачать

Виды и свойства выпуклых четырехугольников
Сумма углов выпуклого четырехугольника равна 360 градусов.
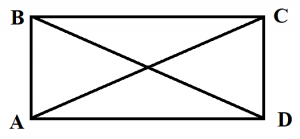
Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы прямые.

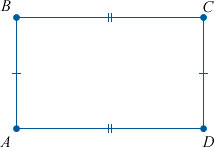
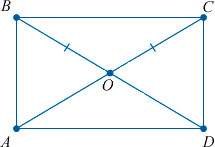
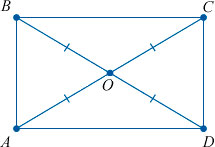
- Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
- Диагонали прямоугольника равны (АС=ВD).
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
- Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:
S=ab, где a и b соседние стороны прямоугольника.
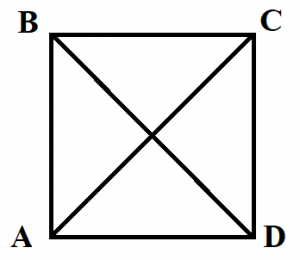
Квадрат
Квадрат – это прямоугольник, у которого все стороны равны.
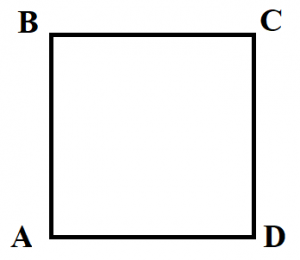
- Диагонали квадрата равны (BD=AC).
- Диагонали квадрата пересекаются под углом 90 градусов.
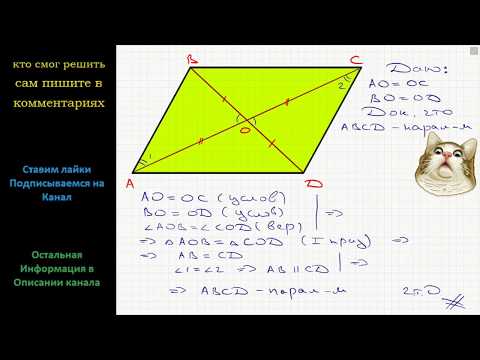
- Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
- Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
- Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.
Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Ромб – это параллелограмм, у которого все стороны равны.
Трапеция
Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.
Виды трапеций
Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.
углы А и С равны по 90 градусов
Средняя линия трапеции
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.
Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.
Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).
Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .
Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.
Для нахождения площади трапеции в справочном материале есть формула
S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63
pазбирался: Даниил Романович | обсудить разбор | оценить
Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.
Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.
Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8= d 1 × 16 × 2 5 . . 2 . .
В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .
Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4
pазбирался: Даниил Романович | обсудить разбор | оценить
На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).
Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.
Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).
Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Видео:Если диагонали параллелограмма равны, то это прямоугольник. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Тест по геометрии «Четырехугольники»
Видео:Диагонали четырехугольника равны 4 и 5.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Стопичева Вера Ивановна, учитель математики МОУ Иловская СОШ им. Героя России В. Бурцева
Видео:ЕГЭ Математика Задание 6#27845Скачать

Тест по теме «Четырехугольники» 8 класс
Видео:Найдите длину диагонали четырехугольникаСкачать
Пояснительная записка к тесту по теме
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

«Четырехугольники» 8 класс.
Видео:№410. Является ли четырехугольник квадратом, если его диагонали: а) равны и взаимноСкачать

Тест рассчитан на 5 — 10 минут, в зависимости от подготовленности обучающихся. Рекомендуется провести его после изучения темы «Четырехугольники». Так же можно выполнить задания теста при подготовке к ОГЭ по математике.
Видео:Прямоугольник. 8 класс.Скачать

Вариант 1.
Укажите, какие из перечисленных ниже утверждений верны:
1) Если диагонали четырехугольника равны, то он прямоугольник.
2) Если противоположные стороны четырехугольника попарно равны, то он параллелограмм.
3) Если диагонали четырехугольника перпендикулярны, то он ромб.
4) Диагонали прямоугольника являются биссектрисами его углов.
Площадь прямоугольника АВСD равна 35. Найдите сторону ВС прямоугольника, если известно, что АВ = 5.
1) 7 2) 10 3) 3 4) 5
1) 70° 2) 110° 3) 145° 4) 125°
4. Сторона ромба равна 10 , а одна из его диагоналей равна 12 . Площадь ромба равна:
1)30 2) 24 3) 96 4) 24
5. Площадь квадрата со стороной 7 
1) 14 2) 98 3) 49 4) 20
Видео:8 класс, 7 урок, ПрямоугольникСкачать

Вариант 2.
1. Укажите, какие из перечисленных ниже утверждений верны:
1) Если диагонали четырехугольника равны и точкой пересечения делятся пополам, то он прямоугольник.
2) Если противоположные стороны четырехугольника попарно равны, то он ромб.
3) Если диагонали четырехугольника перпендикулярны, то он квадрат.
4) Диагонали параллелограмма являются биссектрисами его углов.
2 . Площадь прямоугольника АВСD равна 36. Найдите сторону АВ прямоугольника, если известно, что ВС = 12.
1) 10 2) 2,5 3) 3 4) 5
1) 70° 2) 110° 3) 100° 4) 125
4. Сторона ромба равна 5 , а одна из его диагоналей равна 8 . Площадь ромба равна :
1)30 2) 24 3) 15 4) 12
5. Площадь квадрата со стороной 6 
1) 36 2) 18 3) 100 4) 72
Ответы к тесту по геометрии по теме «Четырехугольники»
Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 971 человек из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 333 человека из 71 региона
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 693 человека из 75 регионов
Ищем педагогов в команду «Инфоурок»
- Стопичева Вера ИвановнаНаписать 1586 13.11.2017
Номер материала: ДБ-860046
- 13.11.2017 1423
- 13.11.2017 423
- 13.11.2017 354
- 13.11.2017 317
- 12.11.2017 360
- 12.11.2017 963
- 12.11.2017 124
- 12.11.2017 366
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов
Время чтения: 1 минута
ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России
Время чтения: 1 минута
Число участников РДШ за 2021 год выросло в три раза
Время чтения: 2 минуты
Минпросвещения готовит рекомендации по построению «идеальной школы»
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:№400. Докажите, что если в четырехугольнике все углы прямые, то четырехугольник — прямоугольник.Скачать

Прямоугольник — это одна из основ геометрии
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.
Название это весьма говорящее, и в нем скрыто официальное определение.
Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.
Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.
Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».
Видео:Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Прямоугольник — это.
Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).
У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.
То есть выглядит это так:
Так вот, прямоугольник в данном случае является частным случаем параллелограмма.
У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.
У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.
Ну, и логично предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.
Видео:8 класс, 4 урок, ПараллелограммСкачать

Признаки прямоугольника
Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.
В случае с прямоугольником их всего три:
- Если один из углов параллелограмма прямой, то данный параллелограмм является прямоугольником.
- Если три угла четырехугольника являются прямыми, то перед нами опять же прямоугольник. При этом нет необходимости доказывать, что четырехугольник является параллелограммом. Это промежуточное звено становится верно само по себе.
- Если диагонали параллелограмма равны между собой, то фигура точно является прямоугольником.
» alt=»»>
Видео:Диагонали прямоугольника равны.Скачать
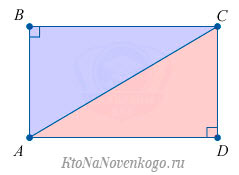
Диагонали прямоугольника
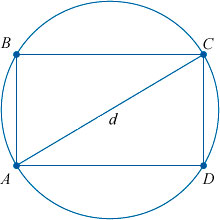
Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.
Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».
В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:
Видео:как найти диагональ.Скачать
Свойства прямоугольника
К свойствам прямоугольника относятся следующие утверждения:
- Прямоугольник является параллелограммом, а значит имеет все присущие ему свойства.
- У прямоугольника равны противоположные стороны.
Видео:Вопрос, который ставит в тупик любого автомобилиста — сколько градусов подъём?Скачать

Периметр и площадь
Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.
Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:
Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:
К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.
Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (5)
Главная основа геометрии — это все же треугольник. Через него можно построить любую фигуру и доказать любую теорему.
Прямоугольник отличается от квадрата, этому учат в школе в младших классах. Квадрат — это одинаковая длина соединяющих углов, если я правильно выражаюсь, а прямоугольник формы может быть: телефон, звуковые колонки, паспорт и прочее.
Не согласен с утверждением, что раз один угол прямой, то перед нами точно прямоугольник, всё же прямоугольник — это когда все противоположные стороны параллельны друг другу, а если только один угол прямой, то там и трапеция может быть.
Я бы сказала, что прямоугольник — это основа архитектуры. Все здания так или иначе используют эту фигуру в своем дизайне.
Вот за что я люблю прямоугольники, так за то, что площадь его легко найти, да и периметр, вот с трапецией сложнее, увы, но те же земельные участки больше трапеции, отсюда и земельные споры.
📺 Видео
Стереометрия 10 класс. Часть 1 | МатематикаСкачать

ОГЭ по математике. Задание 15Скачать

Геометрия Признак параллелограмма: Если в четырехугольнике диагонали точкой пересечения делятсяСкачать