Окружность во фронтальной плоскости

Большинство деталей имеют круглые элементы. Рассмотрим, как во фронтальной диметрической проекции изображаются окружности, плоскости которых соответственно перпендикулярны осям х, у, z.

На рис. 3.10 вычерчено наглядное изображение куба с вписанными в его грани окружностями. Передняя грань куба, параллельная аксонометрической плоскости, проецируется в квадрат, а окружность, вписанная в него, изображается без искажения, т.е. описывается циркулем. Верхняя и боковая стороны куба проецируются в параллелограммы. Поэтому и окружности, вписанные в них, проецируются в эллипсы.

Рис. 3.10. Фронтальные диметрические проекции окружностей, вписанных в грани куба

Изложенное позволяет сделать вывод, что фронтальную проекцию тел вращения целесообразно использовать только в тех случаях, когда деталь можно расположить так, чтобы окружности изображались без искажения и, следовательно, проводились циркулем.

На рис. 3.11 построена фронтальная проекция расположенной подобным образом втулки.

По оси у от точки О отложена высота втулки, сокращенная вдвое (рис. 3.11, а). Из точек О и О1, как из центров, описаны окружности радиусами, равными половине наружного диаметра втулки. К окружностям проведены касательные (они параллельны оси у) (рис. 3.11, б). Из тех же точек О и Οι описаны окружности радиусами, равными половине размера соответствующего отверстия во втулке (рис. 3.11, в). Затем обведен видимый контур (рис. 3.11, г).

Рис. 3.11. Последовательность построения фронтальной диметрической проекции втулки

Видео:Как начертить овал во фронтальной плоскостиСкачать

Прямоугольная изометрическая проекция

Образование изометрической проекции. Если куб расположить так, чтобы три его грани были наклонены под одинаковым углом к аксонометрической плоскости, и проецировать куб на нее с помощью лучей направленных под прямым углом, то образуется изометрическая проекция (рис. 3.12).

Рис. 3.12. Образование изометрической проекции

«Изометрия» (греч.) – равное измерение. При вычерчивании изометрической проекции размеры по всем трем осям для простоты построения откладывают без сокращения, т.е. натуральные.

Расположение осей х, у, z в изометрической проекции и способ их построения показаны на рис. 3.13. Ось z проводят вертикально, а оси х и у – под углом 30° к горизонтали.

Рис. 3.13. Построение осей изометрической проекции с помощью циркуля

Чтобы построить оси с помощью циркуля и линейки, нужно: из точки О, как из центра, описать дугу любого радиуса; из точки пересечения этой дуги с осью z сделать на дуге тем же раствором циркуля две засечки; точку О соединить прямыми линиями с полученными с помощью засечек точками.

Удобно строить оси и выполнять изометрическую проекцию, пользуясь угольниками с углами 30 и 60°.

Порядок построения изометрических проекций. На рис. 3.14 показано построение изометрической проекции плоской фигуры – правильного шестиугольника (рис. 3.14, а). Для построения вычерчивают изометрические оси х, у, г. Из точки Ο1 по оси х откладывают отрезки O111 и O141 равные размеру отрезков O1 и O4. По этой же оси откладывают отрезки O171 и O181, равные отрезкам O7 и O8. Через полученные точки 71 и 81 проводят параллельно оси у прямые линии. На них откладывают отрезки 71–21, 81–31 и т.д., равные отрезкам 7–2, 8–3 и т.д. Найденные шесть точек последовательно соединяют прямыми (рис. 3.14, б).

Рис. 3.14. Построение изометрической проекции правильного шестиугольника

Построив изометрическую проекцию плоской фигуры, нетрудно вычертить и наглядное изображение призмы, основанием которой она является. Для этого нужно, так же как при построении фронтальной диметрической проекции треугольной призмы (см. рис. 3.6), восставить перпендикуляры из вершин основания (в примере из точек 11, 21, 31, 41, 51, 61) и провести параллельно ребрам нижнего основания ребра верхнего основания.

На рис. 3.15 показаны этапы построения изометрической проекции предмета, чертеж которого приведен на рис. 3.5, а. Вычерчены изометрические оси х, у, z. В плоскости хОу построена передняя грань предмета (рис. 3.15, а). Затем из всех вершин полученной фигуры проведены прямые, параллельные оси у (рис. 3.15, б), так как боковые ребра призмы перпендикулярны передней грани. По оси у отложен отрезок 60 мм и проведены линии, параллельные ребрам передней грани. После этого обведен видимый контур и проставлены размеры (рис. 3.15, в).

Рис. 3.15. Порядок построения изометрической проекции предмета

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Построение окружности в горизонтальной плоскости

Рассмотрим построение перспективы окружности по восьми точкам. Суть способа заключается во вписанной в квадрат ABCD (рис.2.23,а) окружности. Тогда четыре точки касания сторон квадрата (1, 3, 5 и 7) и четыре точки пересечения диагоналей квадрата с окружностью (2, 4, 6 и 8) дают искомые 8 точек для построения перспективы окружности.

Точки 1, 3, 5 и 7 имеются при условии, что перспектива квадрата построена. Для нахождения точек 2, 4, 6 и 8 воспользуемся следующей зависимостью.

Из соотношения подобных треугольников AOl и 20Е:

Из прямоугольного равнобедренного треугольника А19 с углами при вершинах А и 1, равными 45° (рис.2.23,а), величина [1,9]=

Чтобы получить точки 2 и 8, необходимо из точек А и 1 провести прямые под углами 45° к прямой AD, получить точку 9, а затем провести окружность радиусом [1,9]. При пересечении с AD эта окружность даст точки 10 и 11. Дальнейшее построение точек 2, 4, 6 и 8 видно из рис.2.23,а.

Еще проще доказать, что [2,Е]=[1,9], можно, рассмотрев треугольники 02Е и А19. Они равны, так как они прямоугольные, равны их гипотенузы [0,2]=[А,1], а сами треугольники равнобедренные. Отсюда [2,Е]=[1,9].

Построим перспективу квадрата.

Пусть квадрат принадлежит предметной плоскости П], а две его стороны параллельны основанию картины х-х, при этом сторона AD принадлежит (для упрощения) основанию картины (рис.2.23,б). Две другие стороны будут перпендикулярны лг-л;, поэтому они будут иметь точку схода в главной точке Р.

Отмечаем на основании картины л;-* точки А’ и D Это — первая сторона квадрата. Проводим А’Р и D’P. Получили направления еще двух сторон квадрата.

Включаем в рассмотрение дистанционные точки D 1 и D 2 . Поскольку диагонали квадрата проходят под углом 45° к основанию картины, то их точками схода будут дистанционные точки D 1 и D 2 . Проводим прямые A’D 1 и D’D 2 .

Соединив построенные вершины квадрата, получаем его перспективу: A’B’C’D’.

На стороне квадрата A’D’ (рис.2.23,б) строим конфигурацию с рис.2.23,а для получения точек 10 и 11. Так как прямые (10,4) и (11,6) имеют точки схода в главной точке картины, проводим (10,Р) и (11,Р). Пересекаясь с перспективами диагоналей квадрата, эти прямые дают искомые 2, 4, 6 и 8 точки.

Соединяем плавной кривой точки 1, 2, 3, 4, 5, 6, 7, и 8. В результате должен получиться эллипс (см. рис.2.23,б).

Нужно сказать, что центр окружности О не совпадает с центром эллипса. А большой диаметр эллипса не является горизонтальной прямой, если центр окружности не лежит на линии PP].

Если центр окружности находится правее линии РР_Ь то большая ось эллипса будет развернута по часовой стрелке (см. рис.2.24) и тем больше, чем дальше центр от линии РРь И наоборот, если центр окружности расположен левее линии РР_Ь то ось эллипса будет развернута против часовой стрелки.

Для более точного построения эллипса необходимо знать, что в точках 2, 4, 6 и 8 он должен касаться (а не пересекать) прямых, проведенных через эти точки параллельно соответствующим диагоналям квадрата. На рис.2.23 такая прямая (12,8) проведена для точки 8. Точку 12 можно построить, отложив отрезок [11,12]=[11,D] и соединив точку 12 с точкой 8. Прямые (12,8) и (А,С) параллельны (рис.2.23,а), поэтому на перспективе (рис.2.23,б) они сходятся в одной точке — D 1 .

На перспективе (рис.2.23,б) находим точку 12 (для этого можно построить окружность с центром в точке 11 радиусом 111,D |), соединяем ее с точкой 8 или с дистанционной точкой D 1 . Этой прямой (12JD 1 ) должен касаться строящийся эллипс.

Другие прямые, которых должен касаться эллипс, строятся аналогично. Или точки 2 и 6 соединяются с дистанционной точкой D 2 , а точки 4 и 8 — с D 1 , или строятся соответствующие окружности, наподобие той, что была построена для определения точки 12.

Построим две окружности в перспективе, одна из которых расположена прямо перед наблюдателем так, что ее центр находится на линии PP], а другая — правее, но так же, как и первая, касается основания картины.

Обе перспективы построены по восьми точкам. Видно, что если первая окружность имеет вид эллипса, у которой большой диаметр параллелен основанию картины, то большой диаметр второго эллипса имеет острый угол с основанием картины. Искажение второго эллипса объясняется недопустимо большим углом зрения, под которым она построена. Поэтому, если нельзя уменьшить угол зрения, надо изображение скорректировать, изобразив вторую окружность как и первую (на рис.2.23 скорректированная перспектива второй окружности изображена штриховой линией).

Видео:КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

Построение окружности в профильной плоскости

В вертикальной плоскости окружность по восьми точкам строится аналогично (рис.2.24).

Сначала строим перспективу квадрата в горизонтальной плоскости, а затем в профильной. При этом [А’,Е’]= [A’,D’]. Найдя центр горизонтальной окружности О и точку 2, строим профильные проекции восьми точек, как показано на рис.2.24.

Видео:2 2 3 построение изометрии окружностиСкачать

Построение окружности во фронтальной плоскости

Окружность во фронтальной плоскости (плоскости, параллельной картине) имеет перспективу в виде окружности. Если окружность находится в картинной плоскости, то ее перспективное изображение совпадает с самой окружностью, и диаметр перспективы окружности равен диаметру самой окружности. По мере удаления от наблюдателя диаметр перспективы окружности уменьшается.

На рис.2.25 показаны четыре окружности, плоскости которых параллельны картине, а центры находятся на прямой, перпендикулярной картине. Перспектива этой прямой — [0′,Р].

Первая окружность с центром в точке О расположена в картинной плоскости. Остальные окружности равны ей по диаметру.

Видео:Компьютерная графика. 9 урок. Окружность в изометрии на фронтальной плоскостиСкачать

Построение окружности в начертательной геометрии с примером

Построение окружности:

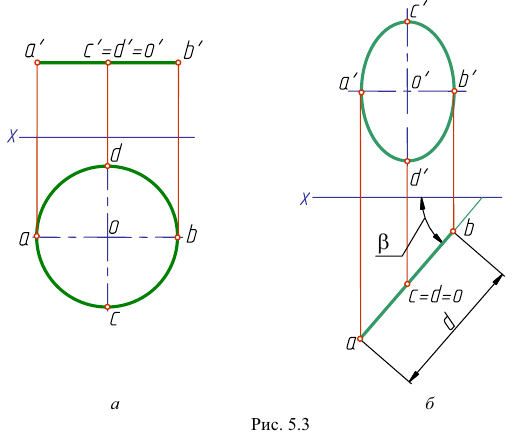
Окружность — плоская кривая второго порядка, ортогональная проекция которой может быть окружностью и эллипсом (рис. 5.3).

Для изображения окружности диаметра d на комплексном чертеже обязательно строят проекции центра О и двух ее диаметров.

Если окружность расположена в плоскости уровня, например в плоскости, параллельной плоскости Н (рис. 5.3, а), то в этом случае фронтальной проекцией окружности служит отрезок, равный d, а гори­ зонтальной проекцией является окружность.

Если окружность расположена в проецирующей плоскости, то проекции ее диаметров параллельны плоскостям проекций. Например,

Если окружность расположена в плоскости общего положения, она проецируется на все плоскости проекций в виде эллипсов, которые можно построить по сопряженным диаметрам. Эти диаметры являются проекциями диаметров, параллельных плоскостям проекций.

• Цилиндрическая винтовая линия
• Определение и задание поверхностей на чертеже
• Классификация поверхностей
• Пересечение многогранников плоскостями
• Взаимное положение двух плоскостей, прямой линии и плоскости
• Решение задач на тему: перпендикулярности прямой и плоскости
• Проекции с числовыми отметками
• Перспектива

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

🔥 Видео

Построение окружности в диметрииСкачать

Прямоугольные диметрические проекцииСкачать

ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Окружность в изометрии ZXСкачать

Построение недостающих проекции сквозного отверстия в сфереСкачать

10 класс, 11 урок, Числовая окружностьСкачать

КАК РИСОВАТЬ ЭЛЛИПСЫ. Простой и быстрый способ рисования ЭЛЛИПСОВСкачать

Д.О. Технология 8 кл. Аксонометрическая проекция плоскогранных предметов. И.М.МазаеваСкачать

Изометрия. Овалы. Два способа построения.Скачать

Построение аксонометрии моделиСкачать

Проекции окружности расположенной в плоскости общего положения. Метод вращенияСкачать

Окружность в изометрииСкачать

Как начертить овал в профильной плоскостиСкачать

окружность в изометрии ХYСкачать

2 3 проекция точки на конусеСкачать