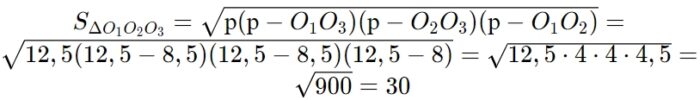Доказать треугольник авс а1в1с1

Вопрос по геометрии:

Доказать что треугольник АВС подобен треугольнику А1 В1 С1(вот картинка)

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

В треугольнике abc угол B=180-50-60=70 градусов
В треугольнике A1B1C1 угол A1=180-70-60=50 градусов
угол А=углу А1, угол В=углу В1, угол С= углу С1 =>
треугольники подобны по трем углам

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:№141. В треугольниках ABC и А1В1С1 отрезки AD и A1D1 — биссектрисы, АВ=А1В1, BD = B1D1 и AD=A1D1.Скачать

Докажите, что треугольники ABC и А1B1С1 равны, если АВ =А1В1, ∠A=∠A1, AD =A1D1, где AD и A1D1 — биссектрисы треугольников

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Ваш ответ

Видео:№176* Докажите, что треугольники ABC и А1В1С1 равны, если АВ=А1В1, АС=А1С1, АМ=А1М1, где AM и А1М1Скачать

решение вопроса

Видео:№177* Даны два треугольника: ABC и А1В1С1. Известно, что АВ=А1В1, АС=А1С1, ∠A=∠A1. На сторонах АССкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,049
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№140. В треугольниках ABC и А1B1С1 медианы ВМ и B1М1 равны, АВ =А1B1, АС=А1С1. Докажите, что ΔABCСкачать

Решение №2664 Точки A1, B1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС.

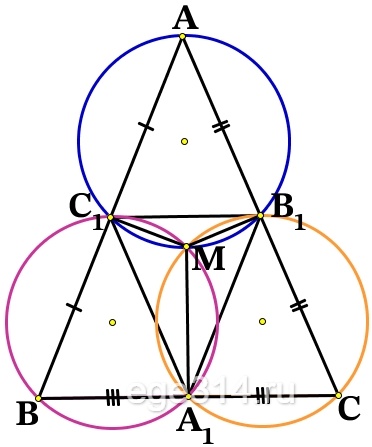
Точки A₁, B₁, С₁ – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС.
а) Докажите, что окружности, описанные около треугольников А₁СВ₁, А₁ВС₁ и В₁АС₁ пересекаются в одной точке.
б) Известно, что АВ = АС = 17 и ВС = 16. Найдите радиус окружности, вписанной в треугольник, вершины которого – центры окружностей, описанных около треугольников А₁СВ₁, А₁ВС₁ и В₁АС₁.

Источник: Ященко ЕГЭ 2022 (36 вар)

а) Пусть М – отличная от А₁ точка пересечения окружностей (двух), описанных около треугольников ΔА₁ВС₁ и ΔA₁CB₁.

Четырёхугольник А₁ВС₁М вписан в окружность, поэтому сумма его противолежащих углов равна 180°, выразим ∠А₁МС₁:

Аналогично для четырёхугольника А₁СВ₁М:

∠В₁МС₁ = 360° – (∠А₁МС₁ + ∠А₁МВ₁) = 360° – ( 180° – ∠В + 180° – ∠С) = 360° – 360° + ∠В + ∠С = ∠В + ∠С

Сумма углов любого треугольника равна 180° (ΔАВС), тогда:

∠В₁МС₁ = ∠В + ∠С = 180° – ∠А

Т.к. у четырёхугольника В₁АС₁М сумма противоположных углов равна 180° (∠А+ ∠В₁МС₁ = 180°, а значит и ∠АС₁М + ∠АВ₁М = 180°), значит он тоже вписанный в окружность.
Следовательно, точка М лежит и на описанной окружности (третьей) треугольника ΔB₁AC₁. Значит все три окружности пересекаются в одной точке М.
Что и требовалось доказать.

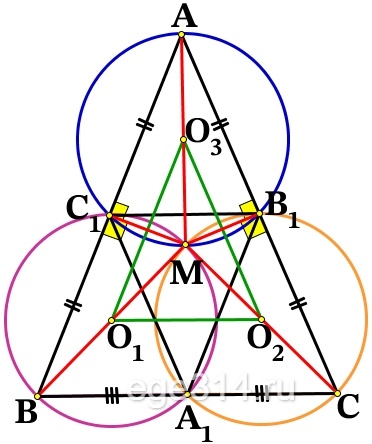
б) АВ = АС = 17, ВС = 16, найти r окружности вписанной в ΔО₁О₂О₃ , где О₁, О₂, О₃ центры окружностей описанных около А₁ВС₁, А₁СВ₁ и В₁АС₁ соответственно:

Радиус окружности вписанной в ΔО₁О₂О₃ можно найди по формуле:

По условию АВ = АС, тогда и АС₁ = АВ₁, значит ΔАС₁В₁ равнобедренный ⇒ АМ диаметр окружности описанной около равнобедренного треугольника.
Поэтому отрезок МВ₁⊥АС (т.к. ΔАМВ₁ вписанный опирающийся на диаметр, а значит прямоугольный), значит СМ тоже диаметр (т.к. ∠МВ₁С = 90°) описанный около треугольника СВ₁А₁.
ΔАМВ₁ = ΔСМВ₁ (МВ₁ – общая, АВ₁ = СВ₁, ∠АВ₁М = ∠СВ₁М = 90°), тогда и соответствующие стороны равны, они же диаметры окружностей:

АМ = СМ

Аналогично для диаметров АМ и ВМ, тогда:

АМ = СМ = ВМ

Получаем три равнобедренных треугольника ΔАМВ, ΔАМС, ВМС, у которых точки О₁, О₂, О₃ середины сторон (как центры окружностей на диаметрах), тогда О₁О₃, О₁О₂, О₂О₃ средние линии, они равны половине соответствующих оснований, найдём их:

По формуле Герона найдём площадь ΔО₁О₂О₃ . Полупериметр равен:

р = Р_Δ/2 = 25/2 = 12,5

Площадь равна:

Найдём искомый радиус r:

🔍 Видео

№262 В треугольниках ABC и А1В1С1 углы А и А1 — прямые, BD и В1D1— биссектрисы. Докажите, чтоСкачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

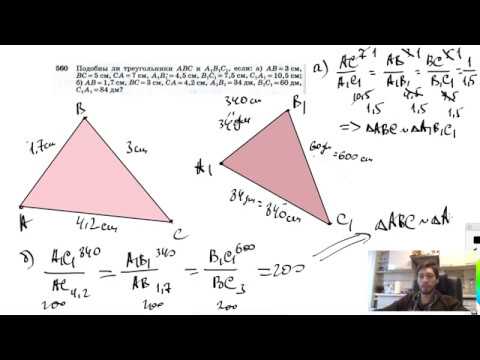
№560. Подобны ли треугольники ABC и A1B1C1, если: а) АВ = 3 см, ВС=5 см, СА=7 см, А1В1=4,5см,Скачать

№545. Треугольники ABC и А1В1С1 подобны, и их сходственные стороны относятся как 6:5Скачать

№269. Докажите, что ΔАВС=ΔА1B1С1, если ∠A=∠A1, ∠B=∠B1 и ВН=В1Н1, где ВН и В1Н1Скачать

№127. В треугольниках ABC и А1В1С1 АВ=А1В1, ВС=В1С1, ∠B =∠B1Скачать

№98. В треугольниках ABC и A1B1C1 AB = А1В1, АС = А1С1, ∠A=∠A1 На сторонах AB и A1B1 отмеченыСкачать

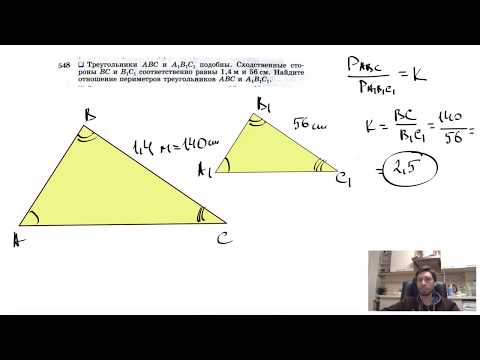
№548. Треугольники ABC и А1В1С1 подобны. Сходственные стороны ВС и В1С1 соответственно равныСкачать

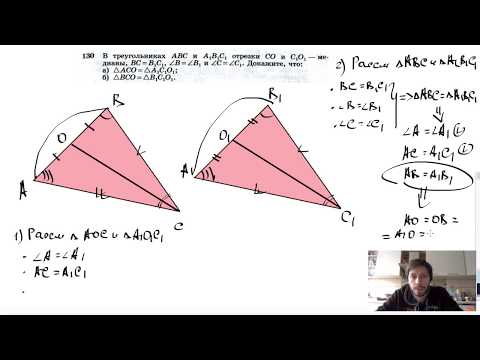
№130. В треугольниках ABC и А1В1С1 отрезки СО и С1О1 — медианы, ВС=В1С1, ∠B = ∠B1 и ∠C=∠C1Скачать

№164. На сторонах равностороннего треугольника ABC отложены равные отрезки AD, BE и CF, как показаноСкачать

№161. В треугольниках ABC и А1B1С1 медианы AM и А1М1 равны, BC=B1С1 и ∠AMB=∠A1M1B1. Докажите, чтоСкачать

№170. Докажите, что треугольники ABC и А1B1С1 равны, если АВ =А1В1, ∠A=∠A1, AD =A1D1, где AD и A1D1Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Признаки равенства треугольников. 7 класс.Скачать