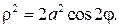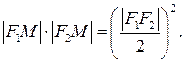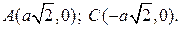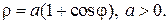$d=sqrt$
НАПРАВЛЯЮЩИЙ КОСИНУС ЛИНИИ, СОЕДИНЯЮЩЕЯ ТОЧКИ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$
$l=cosalpha=frac$, $m=cosbeta=frac$, $n=cosgamma=frac$
где $alpha,beta,gamma$ углы, которые линия $P_1P_2$ образовывает с положительными осями $x,y,z$ соответственно, а $d$ определено на рисунке вверху.
ОТНОШЕНИЕ МЕЖДУ НАПРЯВЛЯЮЩИМИ КОСИНУСАМИ
$cos^2alpha+cos^2beta+cos^2gamma=1$ или $l^2+m^2+n^2=1$
НАПРАВЛЯЮЩИЕ ЧИСЛА
Числа $L,M,N$, которые есть пропорциональны к направляющим косинусам $l, m, n$ называются направляющими числами. Отношение между ними
Это также действительно, если $l, m, n$ заменяются на $L, M, N$ соответственно.
УРАВНЕНИЯ ЛИНИИ, СОЕДИНЯЮЩЕЙ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ
$x=x_1+lt$, $y=y_1+mt$, $z=z_1+nt$
Это также действительно если $l, m, n$ заменяются на $L, M, N$ соответственно.
УГОЛ $phi$ МЕЖДУ ДВУМЯ ЛИНЯМИ С НАПРАВЛЯЮЩИМИ КОСИНУСАМИ $l_1, m_1, n_1$ И $l_2, m_2, n_2$
$cosphi=l_1l_2+m_1m_2+n_1n_2$
ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ
$Ax + By + Cz + D = 0$ [$A, B, C, D$ — константы]
УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКИ $(x_1,y_1,z_1),(x_2,y_2,z_2),(x_3,y_3,z_3)$
$beginx-x_1 & y-y_1 & z-z_1\ x_2-x_1 & y_2-y_1 & z_2-z_1\ x_3-x_1 & y_3-y_1 & z_3-z_1end=0$
$begin y_2-y_1 & z_2-z_1\ y_3-y_1 & z_3-z_1end(x-x_1)$ $+begin z_2-z_1 & x_2-x_1\ z_3-z_1 & x_3-x_1end(y-y_1)$ $+begin x_2-x_1 & y_2-y_1\ x_3-x_1 & y_3-y_1end(z-z_1)=0$
где $a, b, c$ есть пересечения на осях $x, y, z$ соответственно.
Обратите внимание, что направляющие числа для линии, перпендикулярной к плоскости $Ax + By + Cz + D = 0$ есть $A, B, C$.
где знак выбирается так, что расстояние не является отрицательным.
НОРМАЛЬНОЕ УРАВНЕНИЯ ПЛОСКОСТИ
$xcosalpha+ycosbeta+zcosgamma=p$
где $p$ = перпендикулярному расстоянию от $O$ к плоскости в $P$ и $alpha, beta, gamma$ есть углами между $OP$ и положительными осями $x, y, z$.
ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕМЕЩЕНИИ
$left<beginx=x’+x_0\ y=y’+y_0\ z=z’+z_0endright.$ $left<beginx’=x-x_0\ y’=y-y_0\ z’=z-z_0endright.$
где $(x, y, z)$ — старые координаты [т.e. координаты относительно системы xyz], $(x’, y’, z’)$ — новые координаты [относительно системы $x’y’z’$] и $(x_0,y_0,z_0)$ координаты нового центра $O’$ относительно старой координатной системы $xyz$.
ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ВРАЩЕНИИ
где центры систем $xyz$ и $x’y’z’$ находятся в одной точке и $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ направляющие косинусы осей $x’, y’, z’$ относительно осей $x, y, z$ соответственно.
ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕМЕЩЕНИИ И ВРАЩЕНИИ
$left<beginx=l_1x’+l_2y’+l_3z’+x_0\ y=m_1x’+m_2y’+m_3z’+y_0\ z=n_1x’+n_2y’+n_3z’+z_0endright.$
$left<beginx’=l_1(x-x_0)+m_1(y-y_0)+n_1(z-z_0)\ y’=l_2(x-x_0)+m_2(y-y_0)+n_2(z-z_0)\ z’=l_3(x-x_0)+m_3(y-y_0)+n_3(z-z_0)endright.$
где $O’$ системы $x’y’z’$ имеет координаты $(x_0,y_0,z_0)$ относительно системы $xyz$ и $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ направляющие косинусы осей $x’, y’, z’$ относительно осей $x, y, z$ соответственно.
ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ $(r, theta, z)$
Точка $P$ может быть определена как цилиндрическими координатами $(r, theta, z)$, так и прямоугольными координатами $(x, y, z)$.
Преобразование между этими двумя координатами есть
СФЕРИЧЕСКИЕ КООРДИНАТЫ $(r, theta, phi)$
Точка $P$ может быть определена как сферическими координатами $(r, theta, phi)$ так и прямоугольными координатами $(x, y, z)$.
Преобразование между этими двумя кординатами есть
$left<beginx=rsinthetacosphi\ y=rsinthetasinphi\ z=rcosthetaendright.$
УРАВНЕНИЕ СФЕРЫ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
$(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2$
где сфера имеет центр $(x_0,y_0,z_0)$ и радиус $R$.
УРАВНЕНИЕ СФЕРЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
$r^2-2r_0r(theta-theta_0)+r_0^2+(z-z_0)^2=R^2$
где сфера имеет центр $(r_0;theta_0;z_0)$ в цилиндрических координатах и радиус $R$.
Если центр находится в начале координат, уравнение имеет вид:
УРАВНЕНИЕ СФЕРЫ В СФЕРИЧЕСКИХ КООРДИНАТАХ
$r^2+r_0^2-2r_0 rsinthetasintheta_0cos(phi-phi_0)=R^2$
где сфера имеет центр $(r_0; theta_0; phi_0)$ в сферических координатах и радиус $R$.
Если центр в начале координат, уравнение имеет вид:
ЭЛЛИПТИЧЕСКИЙ ЦИЛИНДР С ОСЬЮ КАК $z$ ОСЬ
$frac+frac=1$
где $a, b$ — полуоси эллиптического сечения.
Если $b = a$, фигура превращается в цилиндрический цилиндр с радиусом $a$.
Обратите внимание на ориентацию осей этой фигуры.
- Уравнение окружности в параметрическом виде
- 6. Параметрическое задание линий
- Содержание
- Параметрическое представление функции [ править | править код ]
- Параметрическое представление уравнения [ править | править код ]
- Параметрическое уравнение [ править | править код ]
- Примеры [ править | править код ]
- Уравнения некоторых кривых в параметрической форме:
- Мир трехмерной гиперсферы. Геодезическая трассировка лучей в замкнутой вселенной со сферической геометрией
- Введение. Двухмерный замкнутый мир
- Трехмерный замкнутый мир
- Модель
- Первое знакомство
- Визуальное исследование
- Заключение
- 📺 Видео
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

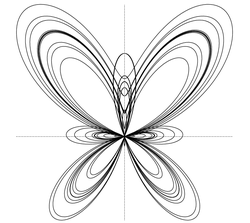
Уравнение окружности в параметрическом виде
Кардиоида
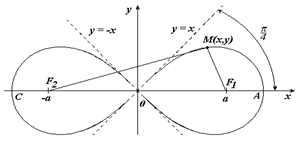
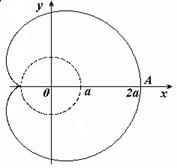
Лемниската Бернулли
Лемниската Бернулли – линия, представляющая геометрическое место точек, расстояние которых от двух данных точек (фокусов) есть постоянная величина, равная квадрату половины межфокусного расстояния.
В полярных координатах
Укажем, что точка М лежит на кривой, если выполнено условие
Вершины кривой находятся в точках
Площадь каждой петли S=a 2 .
В полярных координатах
Вершина кардиоиды находится в точке А(2а,0).
Укажем, что площадь кардиоиды 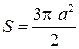
Видео:10 класс, 11 урок, Числовая окружностьСкачать

6. Параметрическое задание линий
Параметрические уравнения линий задаются в виде зависимости текущих координат x и y от некоторого параметра t. Каждому значению t соответствуют два значения: x и y. При изменении параметра t текущая точка M(x,y) описывает некоторую кривую на плоскости.
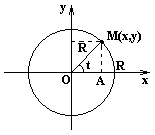 |
Пусть M(x,y) – текущая точка окружности с центром в начале координат и радиусом R. В качестве параметра t выберем угол, который составляет радиус-вектор точки М с осью ox 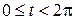
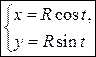
Исключим из параметрических уравнений параметр t. Для этого возведём эти уравнения в квадрат и сложим их:
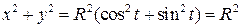
| | | следующая лекция ==> | |
| Четырехлепестковые розы | | | Астроида |
Дата добавления: 2013-12-13 ; Просмотров: 2896 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Параметрическое представление — используемая в математическом анализе разновидность представления переменных, когда их зависимость выражается через дополнительную величину — параметр.
Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Содержание
Видео:Координаты точки в трехмерном пространствеСкачать

Параметрическое представление функции [ править | править код ]
Предположим, что функциональная зависимость y от x не задана непосредственно y = f(x), а через промежуточную величину — t. Тогда формулы
;> 
задают параметрическое представление функции одной переменной.
Если предположить, что обе эти функции φ и ψ имеют производные и для φ существует обратная функция θ, явное представление функции выражается через параметрическое как [1] :
y = ψ ( θ ( x ) ) = f ( x )
и производная функции может быть вычислена как
y ′ ( x ) = d y d x = y t ′ x t ′ = ψ ′ ( t ) ϕ ′ ( t ) >= >>= >
Параметрическое представление даёт такое важное преимущество, что позволяет изучать неявные функции в тех случаях, когда их приведение к явному виду иначе как через параметры затруднительно.
Видео:А.7.19 Поворот в трехмерном пространствеСкачать

Параметрическое представление уравнения [ править | править код ]
Параметрическое представление для более общего случая: когда переменные связаны уравнением (или системы уравнений, если переменных больше двух).
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Параметрическое уравнение [ править | править код ]
Близкое понятие — параметрическое уравнение [2] множества точек, когда координаты точек задаются как функции от некоторого набора свободных параметров. Если параметр один, мы получим параметрическое уравнение кривой.
x = x ( t ) ; y = y ( t ) 

Выражая координаты точек поверхности через два свободных параметра, мы получим параметрическое задание поверхности.
Примеры [ править | править код ]
Уравнение окружности имеет вид:
x 2 + y 2 = r 2 . +y^ =r^ .>
Параметрическое уравнение окружности:
;> 
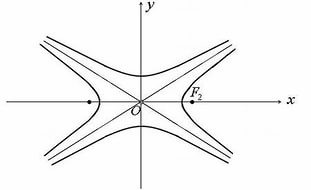
Параметрическое уравнение правой ветви гиперболы :
t> 
Предположим, что функция $x=phi (t)$ имеет обратную функцию $t= (x)$. Тогда справедливо равенство:
Параметрический способ задания функций широко применяется в механике. Так, если в плоскости некоторая материальная точка находится в движении (время $t$), и законы движения проекций этой точки на оси координат известны:
Уравнения являются параметрическими уравнениями траекторий движущейся точки. Исключая временной параметр, получим уравнение траектории в форме $y = f(x)$.
Определить траекторию и место падения груза, сброшенного с самолета, движущегося горизонтально со скорость $v_0$ на высоте $y_0$.
Допустим, что груз сбрасывается с момент пересечения самолетом оси Oy. Тогда очевидно, что горизонтальное перемещение груза равномерно и имеет постоянную скорость:
А вертикальное перемещение:
Следовательно, расстояние от груза до земли в произвольный момент падения:
Уравнения горизонтального и вертикального перемещения тела являются параметрическими. Для того, чтобы исключить временной параметр $t$, найдем его значение из первого уравнения.
Полученное выражение подставим во второе параметрическое уравнение чтобы найти уравнение траектории:
Попробуй обратиться за помощью к преподавателям
Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Уравнения некоторых кривых в параметрической форме:
- Окружность
Параметрические кривые окружности:
Рисунок 1. Окружность и ее параметрические кривые
Уравнение гиперболы имеет вид:
Параметрические кривые гиперболы:
Рисунок 2. Гипербола и ее параметрические кривые
Записать уравнение окружности в параметрическом виде.
- Представим уравнение окружности в виде: [x^ +y^ =r^ ] [x^ +y^ =6^ ]
Значит, радиус $r$ равен 6.
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Записать уравнение гиперболы в параметрическом виде.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
Видео:Окружность. 7 класс.Скачать

Мир трехмерной гиперсферы. Геодезическая трассировка лучей в замкнутой вселенной со сферической геометрией
Хотели посмотреть на мир глазами существа живущего в компактной замкнутой вселенной со сферической геометрией? Посмотреть на мир без ночи? Мир, где на небе виден другой полюс планеты? Мир, где нет разницы между солнечным и лунным затмением? Добро пожаловать под кат!
Введение. Двухмерный замкнутый мир
Для того чтобы лучше понять то, что будет происходить дальше вообразим, что вы двухмерное существо и живете в двухмерном мире представляющем собой сферу. Как вы будете воспринимать ваш мир? Начнем с определения положения тел. Вы можете объявить точку, в которой находитесь, «центром вселенной», выбрать два взаимно перпендикулярных единичных вектора и пользоваться полученной декартовой системой координат в окрестностях «центра вселенной».
Однако, по мере удаления от «центра вселенной» начнут происходить странные вещи. То, что воспринималось вами как перпендикулярные прямые, при определенном удалении от «центра вселенной» превращается в то, что воспринимается вами как параллельные прямые…
… А параллельные прямые пересекаются.
Причина проста — то, что воспринимается вами как прямая, на самом деле является большой окружностью — геодезической линией сферы. Поэтому декартова система координат непригодна для определения положения тел в вашем мире — при удалении от «центра вселенной» она теряет смысл.
Вам придется выбрать другую, более подходящую для использования в вашем мире, систему координат — полярную. Эта система координат естественна и непротиворечива. Действительно — угол между полярной осью и направлением на тело остается постоянным вне зависимости от расстояния до тела.
Умея определять положение тел, мы можем мысленно исследовать ваш мир и описать некоторые эффекты, проявляющиеся по мере удаления от «центра вселенной» и обусловленные тем, что ваш мир представляет собой сферу.
Обратная перспектива. Обычно при удалении тела от «центра вселенной» его угловой размер уменьшается. Однако, на расстоянии больше чем четверть длины геодезической линии от «центра вселенной» при удалении тела его угловой размер будет увеличиваться. Этот эффект связан с тем что расстояние между геодезическими линиями сферы до экватора увеличивается, а после экватора уменьшается. Тело, удаленное на одно и то же расстояние от экватора будет иметь один и тот же угловой размер вне зависимости от того по какую сторону от экватора оно лежит. И этот угловой размер будет больше чем угловой размер тела на экваторе.
Растягивание тела на все небо. Здесь термин все небо используется в значении — все поле зрения двухмерного существа (верхнее и нижнее или переднее и заднее). Если тело находится вблизи точки противоположной «центру вселенной», то куда бы вы ни посмотрели, вы встретитесь взглядом с этим телом. У тела не будет точки, которую невозможно было бы увидеть — каждой точке найдется место на небе. Это предельный случай эффекта обратной перспективы.
Симметричное преобразование тел. Если тело находится на расстоянии больше чем половина длины геодезической линии от «центра вселенной», то вы будете видеть это тело симметрично преобразованным — левая и правая стороны тела поменяются местами. Обычно левый и правый лучи выпущенные из «центра вселенной» попадают в левую и правую сторону тела. Однако, на расстоянии половины длины геодезической линии от «центра вселенной» лучи пересекаются и после пересечения попадают в противоположные стороны тела.
Вторая прямая и обратная перспективы. Этот эффект так же наблюдается если тело находится на расстоянии больше чем половина длины геодезической линии от «центра вселенной». На расстояниях от половины до трех четвертей длины геодезической линии от «центра вселенной» при удалении тела его угловой размер снова будет уменьшаться (прямая перспектива). На расстояниях от трех четвертей до целой длины геодезической линии от «центра вселенной» при удалении тела его угловой размер снова будет увеличиваться (обратная перспектива). Этот эффект, как и эффект обратной перспективы, связан с изменением расстояния между геодезическими линиями сферы — на обратном пути к «центру вселенной» расстояние между геодезическими линиями сферы до экватора увеличивается, а после экватора уменьшается.
Двойники. У каждого тела в вашем мире будет двойник — если вы видите перед собой тело, то обернувшись вы сможете увидеть его обратную сторону (двойник). Луч, выпущенный по длинному пути, обходит ваш мир и попадает в обратную сторону тела. Следует отметить, что поверхностью двойника будет та часть поверхности, которую вы не видите перед собой, и она будет симметрично преобразованной. Здесь термин поверхность используется в значении — граница двухмерного тела воспринимаемая двухмерным существом — применительно к кругу фактически речь идет о дуге окружности воспринимаемой двухмерным существом как отрезок, однако, для наглядности, мы будем выделять цветом не только дугу, но и лежащую за ней часть круга.
Прохождение тела через точку противоположную «центру вселенной». Поскольку эффект растягивания тела на все небо является весьма необычным мы рассмотрим его подробнее. На рисунках: окрестность точки противоположной «центру вселенной».
- вначале расположенная перед вами поверхность тела увеличивается (окрашена синим цветом), а расположенная позади вас — уменьшается (окрашена голубым цветом); при этом обе поверхности имеют одинаковые угловые размеры — то есть расположенная перед вами поверхность тела стягивается (все большая часть поверхности лежит в пределах каждого градуса), а расположенная позади вас — растягивается (все меньшая часть поверхности лежит в пределах каждого градуса)
- когда тело касается точки противоположной «центру вселенной» угловой размер обоих поверхностей равен 180 градусам — одну половину неба (перед вами) занимает вся поверхность тела, а вторую половину неба (позади вас) занимает точка, лежащая на обратной стороне тела
- пока центр тела совмещается с точкой противоположной «центру вселенной» происходит процесс обратный стягиванию и растягиванию
- когда тело расположено в точке противоположной «центру вселенной» его поверхность в неискаженном виде растянута на все небо
- сползание тела с точки противоположной «центру вселенной» выглядит аналогично
Двойной горизонт. Представим, что вы живете на двухмерной планете. Опустив взгляд вниз, вы видите поверхность вашей стороны планеты, а подняв взгляд вверх, вы видите… поверхность обратной стороны планеты. Причем она будет очень сильно стянута — видна и поверхность обратной стороны планеты и та часть поверхности вашей стороны планеты, которая находится за вашей спиной за горизонтом — вы можете увидеть все это у себя над головой. Небо будет представлено в виде узкой как ниточка полоски зажатой сверху и снизу горизонтами вашей и обратной сторон планеты. Это комбинация эффекта растягивания тела на все небо и эффекта двойника. Вообще, в вашем мире, если вашему взгляду ничего не мешает, то прямо перед собой можно увидеть свой затылок… здоровый такой затылок, во всех подробностях… растянутый на все небо)
Мир без ночи. Представим, что двухмерная планета на которой вы живете вращается вокруг двухмерной звезды. Свет, испущенный звездой по короткому пути, падает на дневную сторону планеты. В то же время, свет, испущенный звездой по длинному пути, обходит ваш мир и падает на ночную сторону планеты. Ночи больше не существует. Все что осталось — это закаты и рассветы, которые будут происходить одновременно — когда перед вами обращенная к вам сторона звезды начнет заходить за горизонт, позади вас из-за горизонта начнет восходить обратная сторона звезды. Конечно, можно выделить истинные закат и рассвет по длине пути, который прошел свет, но отличить их от двойников будет практически невозможно.
Есть и предельный случай. Если планете не повезло и она находится в точке противоположной звезде, то звезда будет растянута на все небо, но любоваться этим будет проблематично, так как на планету обрушится весь свет испущенный звездой (при отсутствии поглощения и рассеяния света межпланетной средой).
Солнечные и лунные затмения. Представим, что вокруг двухмерной планеты на которой вы живете вращается двухмерный естественный спутник. Когда спутник становится между планетой и звездой его тень падает на планету. С другой стороны в это же время планета становится между светом, испущенным звездой по длинному пути и спутником, то есть тень планеты падает на спутник. Происходит одновременное солнечное и лунное затмения. Конечно, можно выделить истинные солнечное и лунное затмения по длине пути, который прошел свет, но отличить их от двойников будет практически невозможно. Попасть в тень, падающую на планету и ее спутник во время затмений — единственный способ побыть в темноте в вашем мире)
Трехмерный замкнутый мир
Выше мы рассмотрели удивительный мир двухмерного существа. А как насчет нас, трехмерных существ? Какова геометрия Вселенной? К сожалению, наука пока не может дать ответ на этот вопрос. В основном мешают свойства и размер Вселенной. Попробуем помочь науке. Выберем в качестве кандидата наиболее интересную замкнутую вселенную со сферической геометрией и визуально исследуем ее. Будут ли наблюдаться эффекты открытые нами для двухмерного аналога? Может быть, мы узнаем что-то новое? Что-то, чего не ожидали узнать? Или даже увидим то, что видим каждый день, но не обращаем на это внимание? Как вообще будет выглядеть такая вселенная?
Модель
Мы будем исследовать мир, который представляет собой трехмерную гиперсферу (3-сферу) — то есть сферу, лежащую в четырёхмерном пространстве. Выберем один тип объектов для визуализации — сферу (2-сферу принадлежащую 3-сфере).
Декартовы координаты в четырехмерном пространстве — будем обозначать их как — это фактически
.
Гиперсферические координаты в четырехмерном пространстве (используем только углы, так как радиус нашего мира будет константой) — будем обозначать их как — это фактически
.
3-сфера с центром в начале координат — множество точек, радиус-вектор которых имеет длину равную радиусу 3-сферы — это наш мир
2-сфера принадлежащая 3-сфере — множество точек, радиус-вектор которых имеет длину равную радиусу 3-сферы и образует с радиус-вектором центра 2-сферы
угол равный угловому радиусу 2-сферы
— это наши объекты визуализации
— геодезический радиус 2-сферы
Геодезический, угловой и условный радиус — для того что бы лучше понять что это такое рассмотрим двухмерный аналог 2-сферы принадлежащей 3-сфере — окружность принадлежащую сфере.
Красная дуга на рисунке — это геодезический радиус окружности . Красный угол в правой части рисунка — это угловой радиус окружности
. Высота треугольника в правой части рисунка — это условный радиус окружности
.
Переход от гиперсферических координат к декартовым
меняется от
до
меняется от
до
меняется от
до
Пересечение геодезической линии 3-сферы с 2-сферой принадлежащей 3-сфере.
Это соотношение будет использоваться при трассировке лучей. Пусть имеется геодезическая линия выходящая из полюса 3-сферы в направлении определяемом углами
и
— эти углы совпадают с углами определяющими направление в трехмерном пространстве в окрестностях полюса 3-сферы
упростив имеем (1)
подставив (1) в уравнение 2-сферы и упростив имеем (2)
подставив (1) в уравнение 3-сферы и упростив имеем (3)
выразив из (2) имеем
подставив в (3) имеем
Точка на продолжении геодезической линии 3-сферы проходящей через две точки.
Это соотношение будет использоваться при нахождении текстурных координат и внешней нормали в произвольной точке 2-сферы принадлежащей 3-сфере. Пусть
— центр 3-сферы
— центр 2-сферы
— произвольная точка 2-сферы
— искомая точка лежащая на продолжении геодезической линии
на малом угловом расстоянии
от точки
— точка пересечения прямых
и
— точка пересечения прямой проходящей через точку
перпендикулярно прямой
и прямой проходящей через точку
параллельно прямой
— угловой радиус 2-сферы
Если pi$» data-tex=»inline»/>, то следует положить
, а
Найдем
найдем
Мы будем использовать две модели освещения.
Простая модель освещения. В этой модели яркость точки поверхности зависит от косинуса угла между внешней нормалью к поверхности и направлением на наблюдателя. Мы будем использовать ее при построении изображений для пояснительного материала. Фактически — это модель с точечным источником света расположенным там, где находится наблюдатель, в которой яркость точки поверхности не зависит от расстояния до источника света.
Реалистическая модель освещения. В этой модели будет выделенный точечный источник света. Мы будем использовать ее при построении реалистических изображений. Эта модель может учитывать влияние площади волнового фронта на яркость точки поверхности (фактически — влияние расстояния до источника света). В замкнутой вселенной со сферической геометрией площадь волнового фронта прямо пропорциональна квадрату условного радиуса сферы с геодезическим радиусом равным расстоянию от точки поверхности до источника света. При удалении от источника света площадь волнового фронта до экватора увеличивается (лучи света расходятся), а после экватора уменьшается (лучи света сходятся, фокусируются). После прохождения точки противоположной «центру вселенной» происходит обратный процесс: лучи света вначале расходятся, а потом снова сходятся. Кроме того эта модель может учитывать особенности восприятия (закон Вебера — Фехнера).
Для построения изображения будем использовать обратную трассировку лучей. Что бы модель была интерактивной (мы будем осматривать наш мир и перемещаться в нем) изображение должно строиться в режиме реального времени. Поэтому вычисления будем выполнять во фрагментном шейдере (используем WebGL). Интерфейс реализуем на JavaScript.
Первое знакомство
Создадим трехмерный замкнутый мир с длиной геодезической линии равной 100 — так нам будет проще ориентироваться — экватор нашего мира будет расположен от наблюдателя на расстоянии 25 (четверть длины геодезической линии), а противоположный полюс нашего мира — на расстоянии 50 (половина длины геодезической линии). Поместим в наш мир планету и окрасим части ее поверхности в цвета зависящие от того в какой октант они попадают:
| Октант | Знак X | Знак Y | Знак Z | Цвет |
|---|---|---|---|---|
| I | + | + | + | Красный (Red) |
| II | — | + | + | Зеленый (Green) |
| III | — | — | + | Синий (Blue) |
| IV | + | — | + | Оранжевый |
| V | + | + | — | Голубой (Cyan) |
| VI | — | + | — | Пурпурный (Magenta) |
| VII | — | — | — | Желтый (Yellow) |
| VIII | + | — | — | Белый |
В качестве основной текстуры будем использовать текстуру шахматная доска 3×6, то есть каждая параллель и меридиан будут проходить ровно через 12 ячеек. В качестве альтернативной текстуры будем использовать текстуру земной шар. Ниже показаны снимки ознакомительного облета нашей планеты.
Снимок Северного полюса. Ось X направлена вправо, ось Y направлена вверх, ось Z направлена на нас. При наложении альтернативной текстуры можно увидеть:
- справа — Тихий океан
- сверху — Северную Америку
- слева — Атлантический океан
- снизу — Евразию
Снимки перелета от Северного полюса к экватору и от экватора к Южному полюсу.
Снимок Южного полюса. Ось X направлена вправо, ось Y направлена вниз, ось Z направлена от нас. При наложении альтернативной текстуры можно увидеть:
- справа — Тихий океан, Новую Зеландию, Австралию
- сверху — Индийский океан
- слева — Атлантический океан, Африку
- снизу — Южную Америку
Визуальное исследование
Проведем визуальное исследование нашего мира с целью обнаружить аналоги эффектов открытых нами в двухмерном замкнутом мире.
Двойники. Как и в двухмерном аналоге у каждого тела в нашем мире будет двойник — если мы видим перед собой Северный полюс, то обернувшись мы сможем увидеть… Южный полюс. Стягивание поверхности двойника заметно из-за того что мы находимся достаточно близко к планете.
Эксперимент, при котором наблюдатель удаляется от планеты (цифра в левом верхнем углу каждого снимка — это дистанция между наблюдателем и планетой).
- вначале угловой размер планеты уменьшается — это обычная прямая перспектива
- потом, когда планета прошла экватор нашего мира (дистанция более 25), ее угловой размер увеличивается — это знакомый нам эффект обратной перспективы
- при наползании на противоположный полюс нашего мира мы видим стянутую поверхность (дистанция 46,875)
- когда планета находится на противоположном полюсе нашего мира (дистанция 50) ее растягивает на все небо
- при сползании с противоположного полюса нашего мира мы видим растянутую поверхность (дистанция 53,125)
- после того как планета прошла противоположный полюс нашего мира она выглядит симметрично преобразованной — красный октант поменялся с синим и так далее
- затем, угловой размер планеты уменьшается (дистанция от 50 до 75), а потом увеличивается (дистанция от 75 до 100) — это знакомый нам эффект второй прямой и обратной перспективы
Артефакты. При использовании модели было замечено, что во время прохождения планеты через точки лежащие от наблюдателя на расстояниях 25, 50 и 75 возможно появление артефактов — на планете может «вырасти шерсть» или она может вообще «рассыпаться». Видимо моя математика чего-то не учитывает)
Снимок планеты в окрестностях противоположного полюса нашего мира (использован широкоугольный «объектив»). Поверхность планеты перед нами сильно стянута — видно не только все Северное полушарие, но и часть Южного полушария за экватором. Поверхность планеты позади нас сильно растянута — крупно виден Южный полюс. Обе поверхности тянутся друг к другу пытаясь как бы заключить нас в сферическую оболочку и явить нам картину планеты растянутой на все небо.
Эксперимент, при котором наблюдатель поднимает взгляд (цифра в левом верхнем углу каждого снимка — это угол между направлением вниз и направлением взгляда).
- вначале появляется горизонт нашей стороны планеты
- потом, мы видим над ним второй горизонт, где находим то, что расположено на нашей стороне планеты за нашей спиной за горизонтом
- поднимая взгляд выше, мы видим обратную сторону планеты
Снимок двойного горизонта (использован широкоугольный «объектив»). Полоска неба достаточно велика потому что мы находимся на высоте порядка 50 км.
Снимок неба над головой (использован широкоугольный «объектив»).
Мир без ночи.
Далее для простоты мы будем называть нашу планету Землей, ее естественный спутник — Луной, а звезду вокруг которой они обращаются — Солнцем. Пропорции размеров Солнца, Земли, Луны и их орбит для наглядности не будут соблюдены.
На снимке: граница между дневной и ночной сторонами планеты проходящая через Атлантический океан. Одновременно видны убывающая и растущая Земля. Примерно такую картину видят ребята сидящие на лунных базах в нашем мире)
На анимации: движение границы между дневной и ночной сторонами Земли. Видно перекрытие Солнца диском Земли освещенным лучами Солнца выпущенными по длинному пути.
Солнечные и лунные затмения.
На снимке: Луна выходит из тени Земли. Видны границы между дневной и ночной сторонами Земли и Луны.
На анимации: солнечное и лунное затмения.
- вначале Земля отбрасывает тень на Луну, а Луна отбрасывает тень на Землю
- потом Луна выходит из тени Земли, а тень Луны уходит с поверхности Земли
- затем тень Луны возвращается на поверхность Земли и Луна снова заходит в тень Земли
- граница между дневной и ночной сторонами Луны не видна при перекрытии Луны диском Земли потому что обращенная к нам сторона Луны все еще находится в тени Земли
На анимации: движение границ между дневной и ночной сторонами Земли и Луны совмещенное с солнечными и лунными затмениями. Примерно такую картину видят ребята обслуживающие обсерватории в точке Лагранжа L2 в нашем мире) Конечно, если пренебречь вращением Земли)
На снимке: рассвет на МКС в нашем мире)
Заключение
Для чего все это)? Просто очень хотелось посмотреть на мир глазами существа живущего в компактной замкнутой вселенной со сферической геометрией. Познать этот удивительный мир без символов Кристоффеля и тому подобных вещей оставаясь в рамках общего курса высшей математики. Результат перед вами. Кажется все получилось. Надеюсь, вам было интересно и хорошего дня!
Рабочая модель (открывать на ПК, не для мобильных устройств).
Для тех, кого заинтересовала тематика, есть великолепная статья, в которой рассказывается об удивительных явлениях, которые можно наблюдать в реальной Вселенной: Как нарисовать чёрную дыру. Геодезическая трассировка лучей в искривлённом пространстве-времени.
📺 Видео
Стереометрия 10 класс. Часть 1 | МатематикаСкачать

2 2 3 построение изометрии окружностиСкачать

ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Уравнение окружности (1)Скачать

Построение окружности по трём точкам.Скачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

11 класс, 1 урок, Прямоугольная система координат в пространствеСкачать

10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Уравнение окружности ? Окружность в системе координат / Функция окружностиСкачать

Найти центр и радиус окружностиСкачать

Математика это не ИсламСкачать