Окружность в параллельной проекции

Параллельной проекцией окружности является кривая, называемая эллипсом. Так как ортогональная проекция является частным случаем параллельной проекции, то, проецируя окружность О, расположенную в плоскости общего положения Q (рис. 9) ортогонально на плоскость П1 , получаем эллипс О1 .

В окружности проведем два взаимно перпендикулярных диаметра АВ и CD, причем АВ пройдет по прямой уровня плоскости Q, а диаметр CD — по прямой наибольшего уклона этой плоскости по отношению к плоскости проекций П1. Тогда диаметр АВ спроецируется в диаметр А1В1 эллипса, равный диаметру окружности, т.е. АВ=А1В1 , а диаметр CD спроецируется в диаметр C1D1 эллипса. Так как угол, образованный этими диаметрами, является линейным углом двугранного угла наклона плоскости Q к плоскости П1 , то, обозначив его через ц, получим C1D1=CD cosц. Взаимно перпендикулярные окружности диаметры обладают свойством сопряженности (каждый сопряженный диаметр делит пополам хорды, параллельные другому диаметру). Это свойство при параллельном проецировании сохраняется. Следовательно, диаметры А1В1 и C1D1 будут сопряженными диаметрами эллипса. Но, с другой стороны, они взаимно перпендикулярны, поэтому являются осями эллипса, причем А 1В1- большая ось, а C1D1- малая ось.

Проекция треугольника, параллелограмма и трапеции.

Треугольник изображается треугольником любой формы. Медиана треугольника будет изображаться медианой, так как отношение отрезков сохраняется. При проекции биссектрисы и высоты пойдет искажение.

Так как параллельность прямых сохраняется, то изображение параллелограмма, в частности, прямоугольника, ромба, квадрата, служит параллелограмм. Длина сторон и величины углов произвольные.

Любая трапеция изображается в виде произвольной трапеции. Сохраняется только отношение оснований. Равнобокая трапеция имеет ось симметрии. Ее изображают следующим образом (рис. 10). Каждое из оснований делим пополам и проводим ось симметрии.

Проекции правильного шестиугольника.

При построении оригинала правильного шестиугольника используют два симметричных ромба: OBCD и OAFE (рис. 11, а). Изображение же получается при построении ромбов в виде двух одинаковых произвольных параллелограммов. Для получения проекции правильного шестиугольника надо оставшиеся точки соединить (рис. 11, б).

Видео:Параллельное проектирование и его свойства Изображение пространственных фигурСкачать

Изображение окружности при параллельном проектировании

Изображение окружности. Пусть на плоскости П’ задана окружность S(O’, R). Спроектируем ее параллельно прямой т на плоскость П. В этом случае проектирующая прямая опишет цилиндрическую поверхность, которая пересекает плоскость П по эллипсу (рис. 4).

Значит, параллельной проекцией окружности на плоскость П служит эллипс. На основании свойств параллельной проекции можно утверждать, что проекция центра окружности служит центром симметрии эллипса. Центр симметрии эллипса называется центром эллипса. Отрезок, соединяющий две точки эллипса, называется его хордой.

Хорда, проходящая через центр, называется диаметром эллипса. Рассмотрим два взаимно перпендикулярных диаметра [А’В’]и[С’D’] окружности и проведем хорды окружности, параллельные диаметру [А’В’]. Середины этих хорд будут лежать на диаметре [С’D’]. Очевидно, что и диаметр [А’В’] будет делить пополам хорды, параллельные [С’D’]. Это свойство диаметров [А’В’] и [С’D’] называется сопряженностью. При параллельном проектировании диаметры [А’В’] и [С’D’] окружности спроектируются в диаметры эллипса [АВ] и [СD]. При этом свойство перпендикулярности, в общем случае, нарушается, так как оно не является свойством параллельного проектирования, но свойство сопряженности сохраняется.

Итак, взаимно перпендикулярные диаметры окружности проектируются в сопряженные диаметры эллипса. Эллипс имеет только два взаимно перпендикулярных сопряженных диаметра, которые лежат на осях его симметрии. Эти диаметры называются большой и малой осями эллипса.

Касательная l‘ к окружности в точке А’ параллельна диаметру [С’D’], сопряженному диаметру [А’В’]. Она спроектируется в прямую l, которая проходит через точку А, принадлежащую эллипсу, и параллельна диаметру [СD], сопряженному диаметру [АВ].

Такая прямая называется касательной к эллипсу в точке А. Так как подобие плоскости П переводит эллипс в эллипс и сохраняет отношение длин параллельных отрезков, то изображением окружности является произвольный эллипс, причем перпендикулярные диаметры окружности изображаются сопряженными диаметрами этого эллипса.

Задача. Дано изображение окружности в виде эллипса. Построить изображение двух ее взаимно перпендикулярных диаметров.

Рассмотрим два перпендикулярных диаметра [ ] и [ ] окружности (рис. 5а) оригинал). Построим хорду . Параллельное проектирование сохраняет параллельность прямых и отношение отрезков одной прямой. Отсюда вытекает

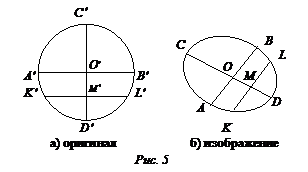
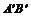
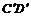
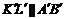
свойство искомых диаметров эллипса: каждый из этих диаметров делит пополам хорды, параллельные другому диаметру. Пользуясь этим свойством, выполним построение. Построим произвольный диаметр [АВ] эллипса (рис. 5б изображение) и параллельную [AB] хорду [KL]. Затем строим середину М этой хорды и проводим через М и О диаметр CD. [AB] и [CD] – диаметры эллипса, изображающие перпендикулярные диаметры окружности. Такие диаметры эллипса называются сопряженными.

Контрольные вопросы и упражнения

1. Треугольник АВС является проекцией треугольника А₁В₁С₁. В треугольнике А₁В₁С₁ проведены из вершины биссектриса, медиана и высота. Будут ли проекции этих отрезков являться биссектрисой, медианой и высотой треугольника АВС?

2. Дано изображение равнобедренного треугольника в виде разностороннего треугольника. На этом изображении постройте:

1) изображение биссектрисы угла при вершине;

2) изображение перпендикуляра к основанию, проведенного через середину боковой стороны.

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Проецирование окружности

Окружность с центром О, рассматриваемая как плоская фигура, проецируется без искажения на ту плоскость, которой она параллельна (рис. 6.5). При этом две другие ее проекции есть отрезки, параллельные осям проекций и равные по длине диаметру окружности.

Если окружность наклонена к плоскости проекций, то ее проекция представляет собой эллипс, большая ось которого равна диаметру окружности. Величина малой оси зависит от угла наклона плоскости окружности к плоскости проекций.

Окружность, изображенная на рис. 6.6, перпендикулярна плоскости проекций П и наклонена к плоскости проекций к₂, поэтому ее фронтальная проекция — эллипс. Большая ось этого эллипса С «И « представляет собой проекцию диаметра окружности, который без искажения проецируется на плоскость проекций л₂. Таким образом, она перпендикулярна плоскости проекций Л1 и параллельна плоскостям проекций 7^2 и Лз. Малая ось эллипса является проекцией диаметра АВ, перпендикулярного СИ. Ее величину на плоскости проекций п₂ определяют с помощью линий проекционной связи, проведенных через точки А’ и В’.

Промежуточные точки эллипса находят с помощью дополнительной плоскости проекций тс₄, которую располагают параллельно плоскости окружности, поэтому окружность проецируется на нее без искажения. Вначале строят новую проекцию центра окружности — точку О™ и на плоскости тс₄ описывают заданную окружность. Затем на окружности намечают 8 или 12 произвольных точек и находят их проекции в системах плоскостей щ/щ и щ/л₂. На рис. 6.6 приведено построение только для двух промежуточных точек 1 и 2; остальные строят аналогично.

Окружность, расположенная в плоскости общего положения, проецируется на все основные плоскости проекций в виде эллипсов, большие оси которых равны ее диаметру. Величины малых осей обычно различны и зависят от углов

наклона заданной плоскости, в которой расположена окружность, к плоскостям проекций.

Если эллипс представляет собой проекцию окружности, то на горизонтальной проекции его большая ось расположена на горизонтальной прямой плоскости, на фронтальной — на фронтальной прямой и на профильной — на профильной прямой.

Построение в плоскости общего положения а(И_а п /_а) (рис. 6.7) проекций окружности с центром в точке О, расположенной на горизонтальной прямой /г_а, и с радиусом, равным /?, начинают с определения проекций осей эллипса.

На горизонтальной проекции окружности по прямой /г_а‘ вправо и влево от точки О‘ откладывают радиус окружности Л, получая при этом точки А’ я В’. Сделав замену плоскостей проекций щ/л2 —> п/щ, где п₄_1_ И_а, и построив новую проекцию окружности в виде отрезка С ,У /) |У , равного диаметру окружности, строят с помощью точек С’ и /)’ малую ось эллипса на горизонтальной проекции (направления построений указаны стрелками).

Для фронтальной проекции окружности через точку О « проводят проекцию прямой, параллельной^’, и на ней вправо и влево от точки О » откладывают радиус окружности Я, получая точки Е «, Е». Сделав замену плоскостей проекций П/П2 —> П2/Л5, где п₅ Е/_а, и построив новую проекцию окружности в виде отрезка, равного диаметру окружности, строят на фронтальной проекции с помощью точек 1У, малую ось эллипса.

Таким образом, на каждой проекции есть по четыре точки, принадлежащие проекции окружности: точки Л ‘, ВС‘, В‘ и Е «, Е», К «, Ь». Проводя из них линии проекционной связи, получают восемь точек для построения горизонтальной и фронтальной проекций эллипса.

📽️ Видео

Изображение фигур в параллельной проекции. Решение задач. Часть 2Скачать

Нахождение истинной формы плоской фигуры методом плоско параллельного перемещенияСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Параллельная проекцияСкачать

тема 8 3 Параллельное проектирование и его свойстваСкачать

Параллельное проектирование и его свойстваСкачать

Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Проектирование.Изображение фигур в пространстве.Часть 1.Скачать

Построение параллельной плоскости на расстояние 30 мм.Скачать

Начертательная геометрия. Методы проецированияСкачать

Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Построение недостающих проекции сквозного отверстия в сфереСкачать

Параллельная ПроекцияСкачать

Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать