Окружность с центром о касается сторон угла 127

Алгебра | 5 — 9 классы

Окружность с центром О касаеться сторон угла с вершиной А в точках В и С Найдите угол ВАС если угол ВОС равен 127 градусов .

Ответ дайте в градусах, единици измерения в ответе не указывайте.

На чертеже получится четырехугольник АОВС, у которого углы В и С — прямые (радиус перпендикулярен касательной в точке касания), а угол О = 127 градусов.

А сумма углов в 4 — хугольнике равна 360 гпадусов.

Значит, угол ВАС = 360 — 90 — 90 — 127 = 53 градуса.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружность с центром О касается сторон угла с вершиной А в точках В и С ?

Окружность с центром О касается сторон угла с вершиной А в точках В и С .

Найдите угол ВАС, если угол ВОС равен 114градусов ?

Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Касательные к окружности с центром O в точках A и B пересекаются под углом 56 градусов?

Касательные к окружности с центром O в точках A и B пересекаются под углом 56 градусов.

Найдите угол ABO.

Ответ дайте в градусах.

Видео:№676. Стороны угла А касаются окружности с центром О радиуса r. Найдите: а) ОА,Скачать

Окружность с центром O касается сторон угла с вершиной A в точках B и C?

Окружность с центром O касается сторон угла с вершиной A в точках B и C.

Найдите угол BAC, если угол BOC равен 127 градусов.

Ответ дайте в градусах.

Видео:В угол C величиной 83° вписана окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Окружность с центром O касается сторон угла с вершиной A в точках B и С?

Окружность с центром O касается сторон угла с вершиной A в точках B и С.

Найдите угол BAC, если угол BOC равен 114 градусов.

Видео:Задача6 №27884 ЕГЭ по математике. Урок 121Скачать

В окружности с центром О АС и ВС — диаметры?

В окружности с центром О АС и ВС — диаметры.

Центральный угол АОD равен 106 градусам.

Найдите вписанный угол АСБ.

Ответ дайте в градусах.

Видео:Окружность с центром на стороне AС треугольника ABC проходит через вершину С и касается прямой AB вСкачать

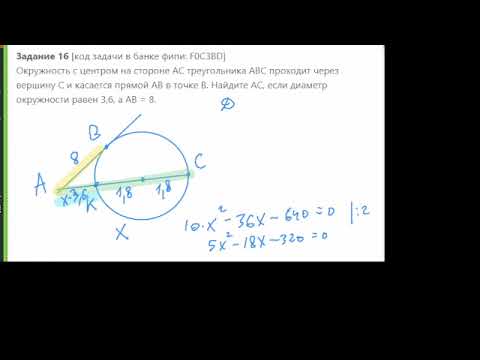
В окружности с центром О отрезки AC и BD диаметры угол aod равен 50° Найдите угол АСВ Ответ дайте в градусах?

В окружности с центром О отрезки AC и BD диаметры угол aod равен 50° Найдите угол АСВ Ответ дайте в градусах.

Видео:🔴 В угол C, равный 165°, вписана окружность с ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

AC и BD — диаметры окружности с центром O?

AC и BD — диаметры окружности с центром O.

Угол ACB равен 34градусов.

Найдите угол AOD.

Ответ дайте в градусах.

Видео:2181 в угол C величиной 79° вписана окружность которая касается сторон углаСкачать

В угол С величиной 72 градуса вписана окружность , которая касается сторон угла в точках А и В, где О — центр окружности?

В угол С величиной 72 градуса вписана окружность , которая касается сторон угла в точках А и В, где О — центр окружности.

Найдите угол АОВ.

Ответ дайте в градусах.

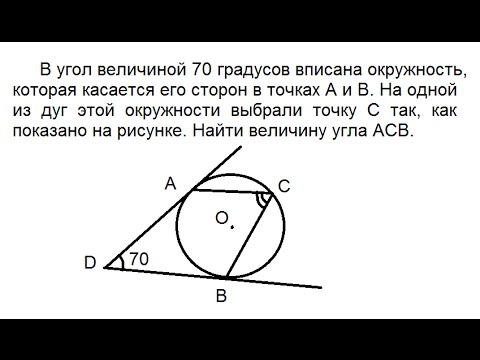
Видео:Видео урок / Геометрия: В угол величиной 70 градусов вписана окружность, которая касается его сторонСкачать

Треугольник АВС вписан в окружность с центром в точке О?

Треугольник АВС вписан в окружность с центром в точке О.

Точки О и С лежат в одной полуплоскости относительно прямой АВ.

Найдите угол АСВ, если угол АОВ равен 167 градусов, ответ дайте в градусах.

Видео:Окружность касается катетовСкачать

В угол С величиной 72° вписана окружность которая касается сторон угла в точках А и В точка О — центр окружности?

В угол С величиной 72° вписана окружность которая касается сторон угла в точках А и В точка О — центр окружности.

Найдите угол АОВ.

Ответ дайте в градусах.

На этой странице вы найдете ответ на вопрос Окружность с центром О касаеться сторон угла с вершиной А в точках В и С Найдите угол ВАС если угол ВОС равен 127 градусов ?. Вопрос соответствует категории Алгебра и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Видео:Геометрия Около треугольника ABC описана окружность с центром O и радиусом, равным 8. НайдитеСкачать

Окружность с центром о касается сторон угла 127

Вопрос по геометрии:

Окружность с центром в точке О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если угол ВОС равен 127 градусов.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 2

угол ВАС=360-ВОС-АВО-АСО=360-127-90-90=53 градуса

360 — 127 — 90 — 90=53 .

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Окружность касается боковых сторон АВ и ВС остроугольного треугольника АВС в точкахА и С соответствеСкачать

Презентация по геометрии » ПЛАНИМЕТРИЯ НА ЕДИНОМ ГОСУДАРСТВЕННОМ ЭКЗАМЕНЕ ПО МАТЕМАТИКЕ»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:🔴 В угол C, равный 79°, вписана окружность ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

ПЛАНИМЕТРИЯ НА ЕДИНОМ ГОСУДАРСТВЕННОМ ЭКЗАМЕНЕ Презентация выполнена по материалам статьи И.К. Варшавского, М.Я.Гаиашвили, Ю.А.Глазкова в журнале « Математика в школе» №2, 2001г.

Во многих задачах встречается окружность, касающаяся сторон угла. Напомним, что в этом случае Центр окружности лежит на биссектрисе угла (О ϵ b). Отрезки, соединяющие точки качания с центром окружности, являются ее радиусами и перпендикулярны к сторонам угла (ОА = ОС = r, ОА ﬩ ВА, ОС ﬩ ВС). Равны расстояния от вершины угла до точек касания (ВА=ВС). ∠АВС + ∠АОС = 180˚. Даже этот краткий перечень свойств позволяет решать большое количество разнообразных задач.

Пример 1 Так как ОА ﬩ ВА, то в треугольнике АВО АВ= =24. Тогда ВА = 24. В треугольнике АВС отрезок ВН – биссектриса и ВА = ВС, следовательно, ВН ﬩ АС и АН = СН. Найдем высоту АН прямоугольного треугольника АВО: АН · ВО = ВА · ОА, значит, = 6,72. Тогда АС = 2АН = 13,44. Ответ: 13,44. Окружность с центром О касается сторон угла В в точках А и С. Радиус окружности равен 7, ВО = 25. Найдите АС. Решение

Пример 2 Окружность с центром О касается сторон угла В в точках А и С. Радиус окружности равен 6, ВО = 2АО. Найдите площадь треугольника АОС. Решение Прежде всего отметим, что на чертеже к данной задаче совсем необязательно изображать окружность, поскольку важно представить лишь взаимное расположение отрезков и точек. В прямоугольнике АВО ВО = 2АО, следовательно, ∠АВО = 30˚. Отсюда получаем: ∠АВС=2∠АВО=60˚ и ∠АОС = 180˚- 60˚ = 120˚. SАОС = АО · СО · = · 36 · = 9 . Ответ: 9 .

Пример 3 Отрезок ВО – биссектриса треугольника АВМ, следовательно, ВА : АО = ВМ : МО = 18 : 9 = 2 : 1. Пусть АО = x, тогда АВ = 2х, и в прямоугольном треугольнике АВМ: 182 = (х + 9)2 + (2х)2. Далее получаем: 5х2 + 18х — 243 = 0. Положительный корень уравнения равен 5,4. Следовательно, АО = 5,4, ВА = 10,8. SВОМ = ВА · ОМ = · 10,8 · 9 = 48,6. Ответ: 48,6. Окружность с центром О касается сторон угла В в точках А и С. Лучи АО и ВС пересекаются в точке М, ОМ = 9, ВМ = 18. Найдите площадь ВОМ. Решение

Пример 4 Окружность с центром О касается сторон угла В в точках А и С. Отрезок ВО пересекает окружность в точке К. Найдите периметр четырехугольника АКСО, если ∠В = 60˚, ВК = 12. Решение Пусть КО = r. В прямоугольном треугольнике АВО ∠АВО= АВС=30˚, следовательно, ВК + КО = 2АО, т.е. ВК + r = 2r. Отсюда получаем: r = ВК = 12. В прямоугольном треугольнике АВО ∠АОВ = 90˚ — ∠АВО = 60˚. Так как в треугольнике АОК ∠О = 60˚ и АО = ОК, то треугольник равносторонний. Значит, АК = r = 12. Аналогично получаем, что СК = r = 12.Итак, периметр четырехугольника АКСО равен 48. Ответ: 48.

Если окружность вписана в треугольник или четырехугольник, то она касается сторон всех его углов, поэтому на основе перечисленных выше свойств окружности, вписанной в угол, получаем: Центр окружности является точкой пересечения биссектрис углов треугольника (четырехугольника). Радиусы, проведенные в точки касания, перпендикулярны к сторонам треугольника (четырехугольника). Равны расстояния от вершины угла до точек касания.

Пример 5 Данная Окружность касается сторон угла А в точках Т и М, следовательно, АТ = АМ. Тогда ВТ = АВ – АТ = АС – АМ = МС. Пусть окружность касается стороны ВС в точке Н. Тогда ВТ = ВН и СМ = СН. Следовательно, ВН = ВТ = СМ = СН = 14 : 2 = 7 и АТ = АМ = 25 – 7 = 18. Так как равнобедренные треугольники АТМ и АВС подобны (почему?), имеем: = . Следовательно, ТМ = = = 10,08. Решение Окружность, вписанная в равнобедренный треугольник АВС, касается его боковых сторон АВ и АС в точках Т и М соответственно. Найдите ТМ, если АВ = 25, ВС = 14. Ответ: 10,08.

Пример 6 Луч ВМ = биссектриса угла В, значит, АМ : СМ = АВ : СВ = 5 : 3. Пусть АМ = 5х, тогда СМ = 3х и АС = 8х. Треугольники АТМ и АВС подобны (почему?), следовательно = , т.е. ТМ = = 3,75. Ответ: 3,75. В треугольник АВС вписана окружность с центром О. Лучи ВО и СО пересекают стороны АС и АВ в точках М и Т соответственно. Найдите МТ, если АВ = АС = 10, ВС = 6. Решение

Пример 7 Пусть луч АО пересекает сторону ВС в точке Н, тогда отрезок АН — биссектриса треугольника АВС. По условию АВ = АС, следовательно, ВН = НС = 8 и АН ﬩ ВС. В прямоугольном треугольнике АВН АН = = 6. Луч ВО – биссектриса угла В, а, значит, отрезок ВО – биссектриса треугольника АВН, поэтому АО : ОН = АВ : ВН = 5 : 4. Пусть АО = 5х, тогда ОН = 4х и АН = 9х. Треугольники АТО и АВН подобны (почему?), следовательно, = . Отсюда получаем: ТО = = = . Значит, ТМ = = 8 . Ответ: 8 . В треугольник АВС вписана окружность с центром О. Прямая, проходящая через точку О параллельно прямой ВС, пересекает стороны АС и АВ в точках М и Т соответственно. Найдите МТ, если АВ = АС = 10, ВС = 16. Решение

. Пример задачи № 7, как и многие геометрические задачи, можно решить несколькими способами. Например, для вычисления отрезка ОН можно использовать формулы S = pr и S = , где S — площадь треугольника, r – радиус вписанной окружности, h — высота треугольника, а – сторона, к которой проведена высота h. Замечание. Возвращаясь к чертежам задач 5, 6 и 7, отметим, что на каждом из них точка М располагается иначе, чем в других задачах (рис. 9). Особенно важно помнить, что в общем случае точка пересечения стороны с биссектрисой треугольника (M1) и точка касания стороны с вписанной окружностью (М2) не совпадают. Их совпадение возможно только на основании равнобедренного треугольника (точка Н). Еще одно интересное соотношение для радиуса окружности, вписанной в равнобедренный треугольник, легко получить, применяя подобие. Рассмотрим равнобедренный треугольник АВС с основанием ВС. Центр окружности лежит на биссектрисе АН, являющейся также высотой и медианой треугольника. Прямоугольные треугольники АОТ и АВН подобны (почему?), следовательно, ТО : ВН = АТ : АН. Из пропорции получаем r = . Аналогично получается формула r = .

Задачи для самостоятельного решения Задача 1. Окружность касается одной стороны прямого угла с вершиной А в точке О и пересекает его вторую сторону в точке С. Найдите радиус окружности, если АВ = 4, АС = 8. Задача 2. Из точки М к окружности с центром О проведены прямая МО и касательная МА (А – точка касания). Из точки А к прямой МО проведен перпендикуляр АВ. Найдите расстояние от точки М до центра, если АМ = 40 и АВ = 24. Задача 3. Через точку внутри круга радиуса 10 проведены две взаимно перпендикулярные хорды длиной 16 и 12. Найдите расстояние между серединами хорд. Задача 4. Две параллельные хорды окружности отсекают от нее дуги в 90˚. Длина одной из хорд равна 8. Найдите расстояние между хордами. Задача 5. Через середину радиуса окружности проведена перпендикулярная ему хорда. Найдите градусную меру меньшей из дуг, на которые окружность делится проведенной хордой. Задача 6. Основание равнобедренного треугольника вдвое меньше его боковой стороны, а высота, проведенная к основанию, равна 10. Найдите радиус вписанной в треугольник окружности. Задача 7. Окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках M и N. Точка М делит сторону на отрезки 18 и 12, считая от основания треугольника. Найдите MN.

Опыт работы показывает, что методика, предложенная авторами, очень помогает при подготовке к ЕГЭ по математике. Учитель: Гудкова В.Д.

🔍 Видео

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Урок 127. Задачи на закон сохранения энергии (ч.2)Скачать

В угол C величиной 157° вписана окружность, которая касается сторон угла в точках A и B, точка OСкачать

Окружность касается сторон параллелограмма и биссектрисы.Скачать

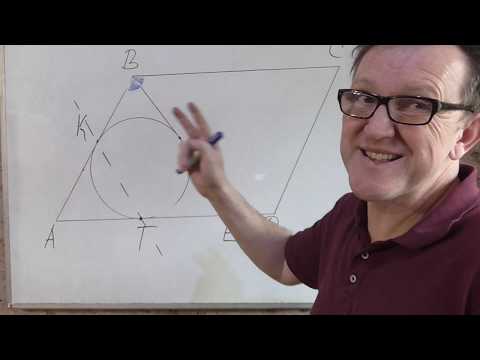
Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать

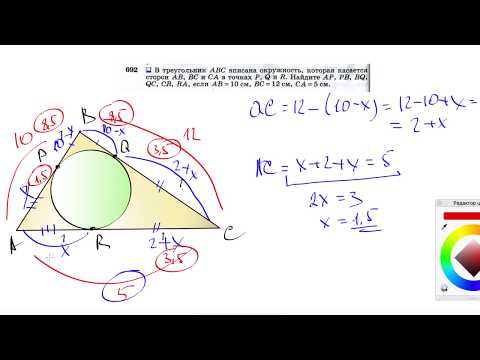
№692. В треугольник ABC вписана окружность, которая касается сторон АВ, ВС и СА в точках Р, Q и RСкачать

🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать