Окружность разделена на равные части найдите

Геометрия | 5 — 9 классы

Окружность разделена на равные части Найдите градусную меру центрального угла а, выделенного цветом.

ТЕОРИЯ (читать всем) : Целая окружность — 360°.

Вписанный угол равен половине дуги, на которую он опирается.

Центральный угол равен дуге, на которую он опирается.

ДАНО : Окружность (О ; r) ; (отмечаем центр окружности буквой О)Окружность разделена на 5 равных частей ; 3 из них закрашены ; НАЙТИ : ∠α — ?

РЕШЕНИЕ : 1) 360 : 5 = 72° — градусная мера одной части окружности ; 2) 72·3 = 216° — градусная мера трёх закрашенных частей ; 3) Так как ∠α центральный, то его градусная мера равна дуге, на которую он опирается.

Дуга, на которую опираются 3 закрашенные части окружности, равна 216.

Видео:Деление окружности на 12 равных частейСкачать

Дуга соответствующая данному центральному углу состовляет 2 / 5 окружности а)найдите градусную и радианную меры центрального угла б)найдите длину дуги если радиус окружности равен 4см?

Дуга соответствующая данному центральному углу состовляет 2 / 5 окружности а)найдите градусную и радианную меры центрального угла б)найдите длину дуги если радиус окружности равен 4см.

Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Найдите градусную меру центрального угла, соответствующего 1 / 6 окружности?

Найдите градусную меру центрального угла, соответствующего 1 / 6 окружности.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Полуокружность разделена на : 1) 3 ; 2) 4 ; 3) 6 ; 4) 18 равных частей?

Полуокружность разделена на : 1) 3 ; 2) 4 ; 3) 6 ; 4) 18 равных частей.

Найдите градусную меру каждой дуги и центрального угла, соответствующего этой дуге.

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Найдите градусную меру центрального угла, соответствующий половины окружности?

Найдите градусную меру центрального угла, соответствующий половины окружности.

Видео:Деление окружности на 3 частиСкачать

1)Окружность разделена на 8 равных частей?

1)Окружность разделена на 8 равных частей.

Определите градусные меры центральных углов.

2)Вписать окружность в равнобедренный треугольник.

3)Расстояние между центрами окружностей равно 5см, радиусы окружностей 4см и 3см.

Каково взаимное расположение окружностей?

Видео:1 2 2 деление окружности на 5 равных частейСкачать

Окружность разделена на 5 равных частей?

Окружность разделена на 5 равных частей.

Найдите градусную меру одного из центральных углов.

Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Найдите центральные углы , если окружность разделена на 9 равных частей ?

Найдите центральные углы , если окружность разделена на 9 равных частей .

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Найдите центральные углы, если окружность разделена на 9 равных частей (желательно с чертежом)?

Найдите центральные углы, если окружность разделена на 9 равных частей (желательно с чертежом).

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Найдите градусную меру центрального угла, соответствующего половине окружности?

Найдите градусную меру центрального угла, соответствующего половине окружности.

Видео:Деление окружности на равные частиСкачать

В окружности дана дуга ВС = 20 градусов?

В окружности дана дуга ВС = 20 градусов.

Найдите ВD = 7 * BC и градусный меру центрального угла BOD этой окружности.

Вопрос Окружность разделена на равные части Найдите градусную меру центрального угла а, выделенного цветом?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

S = (a + b)h / 2 = (6 + 13) * 4 / 2 = 38.

Площадь одной клетки : S1 = 3 * 3 = 9 Фигура занимает 9 клеток, значит, общая площадь : S = 9 * 9 = 81 Ответ : 81.

Опустим высоту из угла 150 градусов на противоположную сторону ромба Получился Прямоуг треуг. Высота будет в треуг являться катетом, который лежит против угла в 30 град (по расчету ромба сумма углов черырехугольника равна 360гр. 2 угла по 150град и..

По формуле V = S * h, где S — площадь основания, h — высота призмы. Здесь h = 5. То естьV = S * 5, V = 5S. Площадь основания треугольника равна по формуле площади правильного треугольника . Здесь а — сторона правильного треугольника. В данном сл..

Просто все время решать задачи. И, например, мы в классе разбираем какую — то задачу, теорему, решаем это, и я пытаюсь не выучить решение задачи, а понять, как она решается. Всякие определения и теоремы нужно конечно учить, но также важно не просто..

1) Угол ECD = C (Друг на друге), ECD = C = 180 — A — B = 41 2) Угол CDE = 180 — угол 3 = 40 3) Угол DEC = 180 — ECD — CDE = 89 4) Угол BDF = CDE (вертикальные) = 40 5) Угол DBF = 180 — угол 1 = 125 6) Угол FBD = 180 — DBF — BDF = 15.

Видео:деление окружности на произвольное число частейСкачать

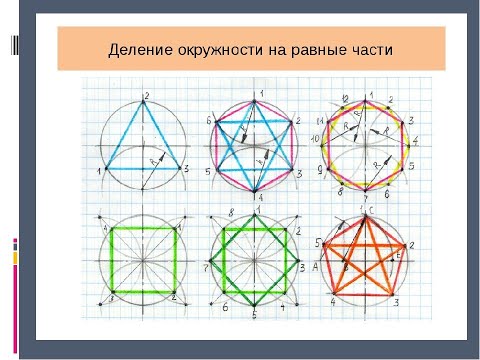
Деление круга на равные части

Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами

Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала — традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним — нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.

Деление круга на равные по площади части радиусами

Деление круга на равные по площади части параллельными хордами

Деление круга на равные части радиусами

Традиционный и очень простой метод деления круга — по факту, нарезка равных секторов. Метод и формулы очень просты:

1. Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.

1. Определяем размер дуги сектора, перемножая радиус на угол в радианах

1. Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.

Собственно и всё — мы получили все характеристики для N равных секторов

Деление круга на равные части параллельными хордами

Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.

Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.

Верхнюю полуокружность можно представить графиком функции y=f(x), где x — это координата вдоль оси абсцисс, а y — это функция, численно равная y координате соответствующей точки верхней полуокружности.

По теореме Пифагора получаем следующую функцию

Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:

Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем

Итак, полное выражение

Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)

Таким образом мы можем приравнять

Что дает нам такое финальное уравнение

Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона.

Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее.

Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.

Видео:Как искать точки на тригонометрической окружности.Скачать

Каждая из данных окружностей разделена на равные части. Найдите градусную меру центральных углов, отмеченных на рисунках.

Видео:Деление окружности на 5 равных частейСкачать

Ваш ответ

Видео:Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

решение вопроса

Видео:Длина окружности. Математика 6 класс.Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,909
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

🎦 Видео

Деление окружности на 4 частиСкачать

Деление окружностей на равные частиСкачать

Длина дуги числовой окружности | Алгебра 10 класс #9 | ИнфоурокСкачать

Деление окружности на равные части с помощью циркуляСкачать

10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать