Окружность проходит через вершины а и с в треугольнике

Условие

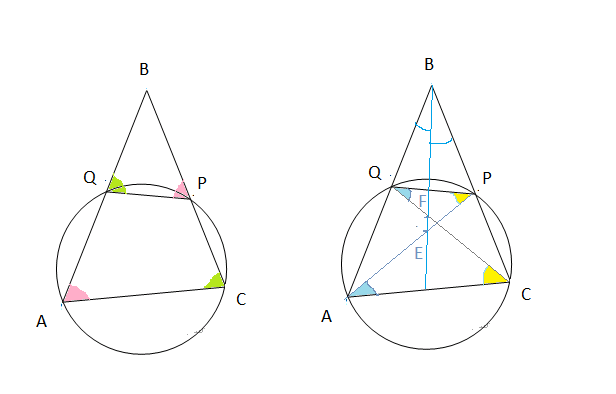
Окружность, проходящая через вершины А и С треугольника АВС, пересекает стороны AB и CB в точках Q и P соответственно. Биссектриса угла ABC пересекает отрезок AP в точке E и отрезок CQ – в точке F. Найдите длину AE, если QF=6, PE=7, CF=9.

Решение

Четырехугольник AQPC вписан в окружность, суммы противолежащих углов равны 180 градусов.
∠ ВАС+ ∠ QPC=180^(o)
Углы
∠ BPQ и ∠ OPC — смежные, их сумма 180 градусов.
Поэтому ∠ ВАС= ∠ BPQ
Аналогично
∠ ВСА= ∠ BQР

Треугольник АВС и AQP подобны по двум углам.
АС:QP=AB:BP=BC:BQ

Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Поэтому
AE:EP=AB:BP(=AC:QP)
и
FC:QF =BC:BQ(=AC:QP)

AE:EP=FC:QF
AE:7=9:6
AE=7*9/6=10,5
О т в е т. 10,5

Видео:Геометрия Окружность проходит через вершины А и С треугольника АВС и пересекает его стороны АВ и ВССкачать

Окружность проходит через вершины А и В треугольника АВС, касается стороны АС в точке А и пересекает сторону ВС в ее середине — точке О?

Геометрия | 10 — 11 классы

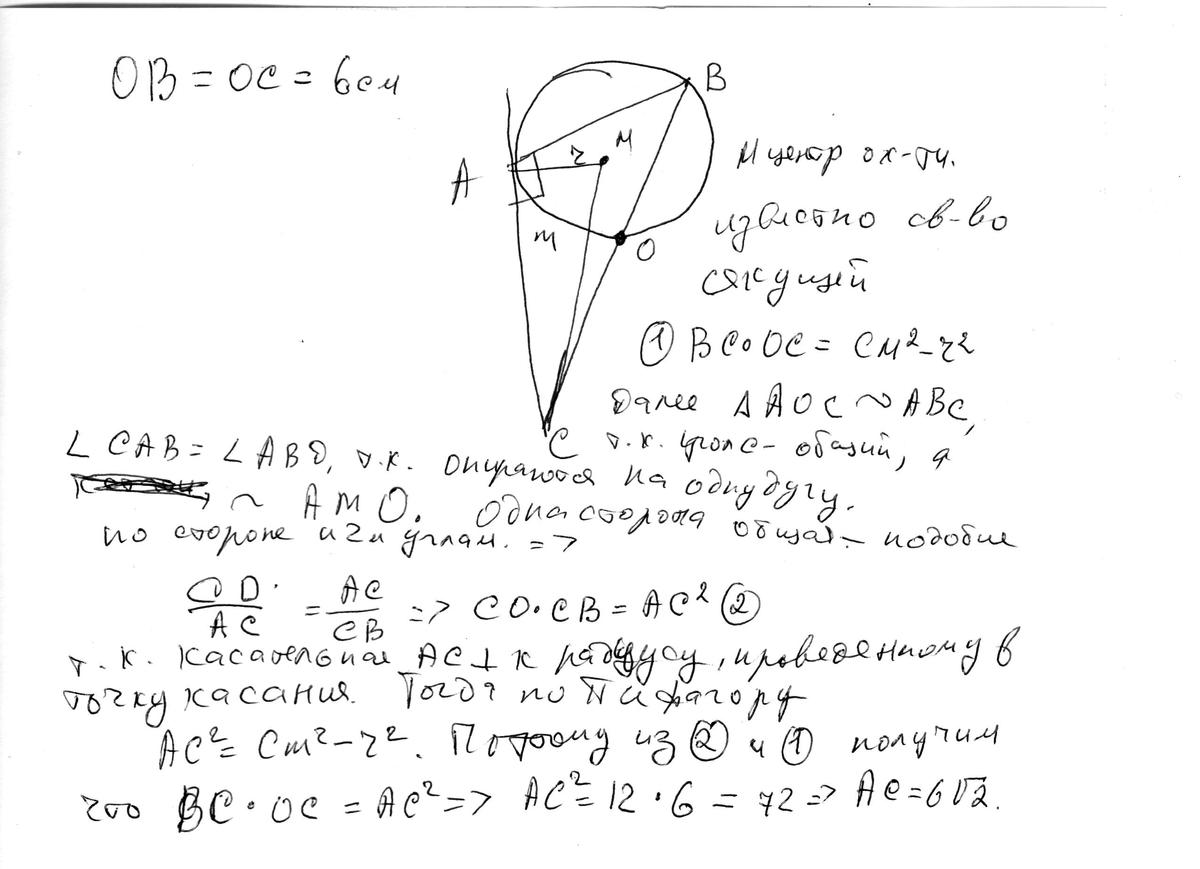
Окружность проходит через вершины А и В треугольника АВС, касается стороны АС в точке А и пересекает сторону ВС в ее середине — точке О.

Вычислите длину стороны АС, если известно, что ОВ = 6см.

Решение в скане.

Видео:Окружность проходит через вершины  A  и  C  треугольника ABC ... ОГЭ, геометрия, часть 11Скачать

В треугольнике АВС известны стороны : АВ = 7, ВС = 10, АС = 8?

В треугольнике АВС известны стороны : АВ = 7, ВС = 10, АС = 8.

Окружность, проходящая Через точки А и С, пересекает прямые ВА и ВС соответственно в точках К и Л, отличных от вершин треугольника.

Отрезок КЛ касается окружности, вписанной в треугольник АВС.

Найдите длину отрезка КЛ.

Видео:Задание 24 ОГЭ по математике #3Скачать

Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В?

Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В.

Найдит5е АС, если диаметр окружности равен 15, а АВ = 4.

Видео:ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

В треугольнике авс на стороне ас как на диаметре построена окружность ?

В треугольнике авс на стороне ас как на диаметре построена окружность .

Эта окружность проходит через середину стороны вс и пересекается в точке д продолжение стороны ав за точку а , причем ад = 0, 25 ас .

Найдите площадь треугольника авс если ав = 1.

Видео:Окружность проходит через вершины А, В и D параллелограммаСкачать

В треугольнике АВС со сторонами АВ = 7см, ВС = 9см, АС = 10см вписана окружность, касающаяся стороны АС в точке Е?

В треугольнике АВС со сторонами АВ = 7см, ВС = 9см, АС = 10см вписана окружность, касающаяся стороны АС в точке Е.

Найдитерасстояние от точки Е до точки К биссектрисы ВК.

Видео:ОГЭ. Задание 24. Геометрическая задача на вычислениеСкачать

В треугольнике АВС известны длины сторон АВ = 14 , АС = 98, точка О — центр окружности , описанной около треугольника АВС ?

В треугольнике АВС известны длины сторон АВ = 14 , АС = 98, точка О — центр окружности , описанной около треугольника АВС .

Прямая ВD, перпендикулярная прямой АО пересекает сторону АС и точке D.

Видео:Разбор Задачи №16 из работы Статград от 29 января 2020 (Запад)Скачать

. Окружность, проходящая через вершины А и В треугольника АВС, пересекает стороны АС и ВС в точках L и K соответственно?

. Окружность, проходящая через вершины А и В треугольника АВС, пересекает стороны АС и ВС в точках L и K соответственно.

Докажите, что треугольники АВС и CKL подобны.

Видео:Окружность с центром на стороне AС треугольника ABC проходит через вершину С и касается прямой AB вСкачать

Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В?

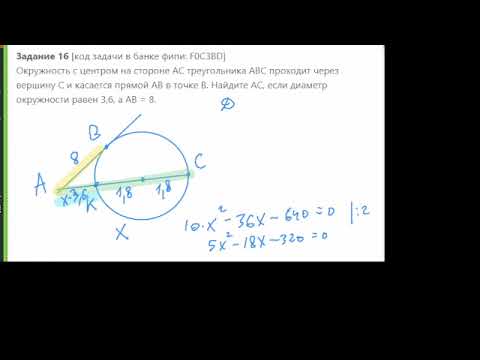
Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В.

Найдите диаметр окружности, если АВ = 2, АС = 8.

Видео:Геометрия. Задача. Треугольник. Окружность.Скачать

В треугольнике АВС известны длины сторон АВ = 32 АС = 64, точка О — центр окружности, описанной около треугольника АВС?

В треугольнике АВС известны длины сторон АВ = 32 АС = 64, точка О — центр окружности, описанной около треугольника АВС.

Прямая ВД, перпендикулярная прямой АО, пересекает сторону АС в точке Д.

Видео:№20. Окружность радиуса R проходит через вершины A, B и C параллелограмма ABCD и второй разСкачать

Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В?

Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В.

Найдите АС, если диаметр окружности равен 5, 25, а АВ = 9.

Видео:Задание 24 ОГЭ по математике #2Скачать

В треугольнике АВС известны длины сторон АВ = 8 и АС = 64?

В треугольнике АВС известны длины сторон АВ = 8 и АС = 64.

Точка О центр окружности, описанной около треугольника АВС.

Прямая ВD перпендикулярная прямой АО , пересекает сторону АС в точке D.

На этой странице находится вопрос Окружность проходит через вершины А и В треугольника АВС, касается стороны АС в точке А и пересекает сторону ВС в ее середине — точке О?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 10 — 11 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

Как — то так, а четвертое, незнаю.

Во — первых, геометрия знакомит нас с окружающей действительностью, в которой многие предметы напоминают различные геометрические фигуры, фактически мы живем в мире геометрии. Во — вторых в равной степени геометрия нужна и математику, и инженеру, и ..

1. Фронтально — проецирующая плоскость 2. Горизонтально — проецирующая плоскость 3. Профильно — проецирующая плоскость 4. Фронтальная плоскость уровня 5. Горизонтальная плоскость уровня 6. Профильная плоскость уровня.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Задание №188

Видео:Математика ОГЭ Задание 25 Первый признак подобияСкачать

Условие

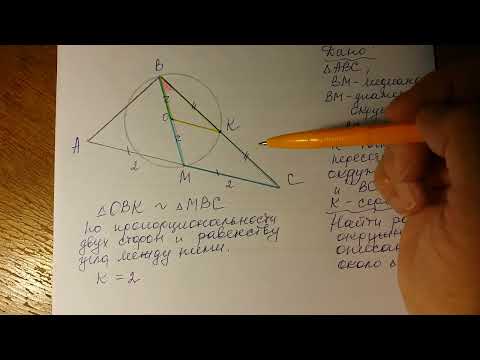
В треугольнике ABC окружность проходит через точки B и C и пересекает стороны AB и AC в точках M и N соответственно. Отрезок MN касается окружности, вписанной в треугольник ABC .

а) Докажите, что bigtriangleup ABC подобен bigtriangleup ANM .

б) Найдите MN , если AB=7, AC=8, BC=9 .

Видео:Задача 23. ОГЭ по математике. Самые важные свойства углов в окружности.Скачать

Решение

а) Окружность с центром в точке O_1 описана около четырехугольника BMNC , значит, angle BCN+angle BMN =180^ , angle BMN=180^-angle BCN . angle AMN+angle BMN=180^ , как смежные, angle BMN=180^-angle AMN.

Отсюда angle BCN=angle AMN .

Имеем в треугольниках ABC и ANM : angle A — общий, angle ACB=angle NCB=angle AMN, значит, bigtriangleup ABC подобен bigtriangleup ANM по первому признаку подобия, что требовалось доказать.

Окружность с центром в точке O вписана в bigtriangleup ABC, значит

AF=AE, BE=BP, CP=CF , как отрезки касательных, проведенных к окружности c центром O_1 из точек A, B и C соответственно.

Пусть AF=AE=x, тогда BE=BP=7-x, CP=CF=8-x, BP+CP=BC, 7-x+8-x=9, x=3, AF=AE=3 .

Обозначим MK=t, NK=p, тогда ME=MK=t, NF=NK=p как отрезки касательных, проведенных к окружности с центром O из точек M и N соответственно.

Получим AM=AE-ME=3-t, AN=AF-NF=3-p, MN=MK+NK=t+p .

Периметр bigtriangleup AMN равен AM+AN+MN=3-t+3-p+t+p=6.

Периметры подобных треугольников относятся так же как и их стороны, поэтому frac=frac, MN=frac=2,25

🌟 Видео

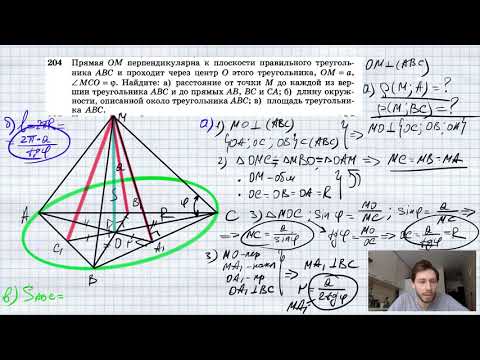
№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать

ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружность проходит через вершины параллелограмма Найдите отношениеСкачать

Урок 3. №23 ОГЭ. Касательная. Окружность с центром на стороне AC касается АВ в точке В.Скачать