Окружность проходит через вершину с прямоугольника авсд (7 видео)

Окружность проходит через вершину А прямоугольника ABCD и касается сторон BC и CD в точках М и Nсоответственно?

Геометрия | 5 — 9 классы

Окружность проходит через вершину А прямоугольника ABCD и касается сторон BC и CD в точках М и Nсоответственно.

Известно, что ВМ = 24, DN = 7.

Найти площадь прямоугольника ABCD.

Решение в файле )).

Содержание

В прямоугольнике ABCD известно, что AB = 4, BC = 9?
Срочно?
В прямоугольнике ABCD сторона AB в два раза больше стороны BC?
Точка S , не лежащая в плоскости прямоугольника ABCD, равноудалена от его сторон?
Смежные стороны прямоугольника ABCD равны 12 см и 14 с?
Прямоугольник ABCD, AB = BC, сторона AC = 4?
Длинна стороны CD прямоугольника ABCD равнв 3 см ?
В прямоугольнике ABCD точка М делит сторону АВ в отношении 2 : 1?
Площадь прямоугольника ABCD равна 18?
Окружность проходит через вершины C и D прямоугольной трапеции ABCD (угол C = углу D = 90 градусам)?
Окружность проходит через вершину с прямоугольника авсд
Окружность проходит через вершину с прямоугольника авсд
🎬 Видео

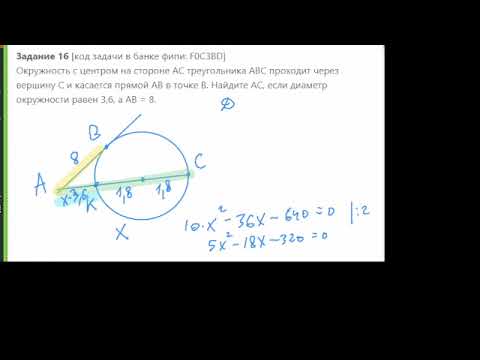
Видео:Окружность с центром на стороне AС треугольника ABC проходит через вершину С и касается прямой AB вСкачать

В прямоугольнике ABCD известно, что AB = 4, BC = 9?

В прямоугольнике ABCD известно, что AB = 4, BC = 9.

Окружность касается сторон AD, CD и пересекает BC в ее середине.

Определите длину отрезка, высекаемого окружностью на стороне BC.

Видео:№150. Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскостиСкачать

Срочно?

Из вершины А прямоугольника АВСD проведен перпендикуляр надиагональ BD, который делит ее на отрезки длиной 9 см и 16 см.

Найти : а) периметр и площадь прямоугольника ABCD ; б) тангенс угла, образованного меньшей стороной и диагональю ; в) радиус окружности, описанной около прямоугольника ABCD.

Видео:№20. Окружность радиуса R проходит через вершины A, B и C параллелограмма ABCD и второй разСкачать

В прямоугольнике ABCD сторона AB в два раза больше стороны BC?

В прямоугольнике ABCD сторона AB в два раза больше стороны BC.

Найдите площадь прямоугольника ABCD, если сторона BC равна 4 см.

Видео:Разбор Задачи №16 из работы Статград от 29 января 2020 (Запад)Скачать

Точка S , не лежащая в плоскости прямоугольника ABCD, равноудалена от его сторон?

Точка S , не лежащая в плоскости прямоугольника ABCD, равноудалена от его сторон.

Найти площадь ABCD, если AC равен 4 корня из 2.

Видео:Задание 24 ОГЭ по математике #2Скачать

Смежные стороны прямоугольника ABCD равны 12 см и 14 с?

Смежные стороны прямоугольника ABCD равны 12 см и 14 с.

Найти площадь прямоугольника.

Видео:ОГЭ. Задание 24. Геометрическая задача на вычислениеСкачать

Прямоугольник ABCD, AB = BC, сторона AC = 4?

Прямоугольник ABCD, AB = BC, сторона AC = 4.

Найти площадь прямоугольника.

Видео:Задание 24 ОГЭ по математике #3Скачать

Длинна стороны CD прямоугольника ABCD равнв 3 см ?

Длинна стороны CD прямоугольника ABCD равнв 3 см .

Окружность с центром в точке A касается прямой BC.

Чему равен радиус окружности?

Видео:ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

В прямоугольнике ABCD точка М делит сторону АВ в отношении 2 : 1?

В прямоугольнике ABCD точка М делит сторону АВ в отношении 2 : 1.

А точка К — середина стороны ВС.

Найти отношение площади треугольника МВК к площади прямоугольника АВСД.

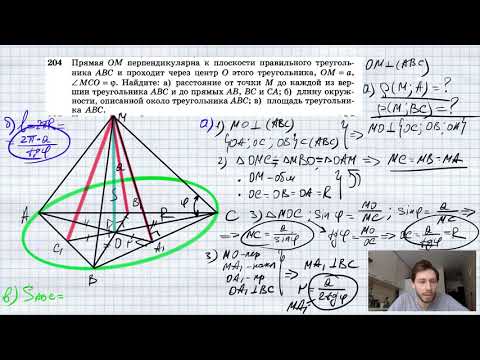
Видео:№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать

Площадь прямоугольника ABCD равна 18?

Площадь прямоугольника ABCD равна 18.

Найти сторону АВ прямоугольника, если известно что ВС = 6.

Видео:ОГЭ без рекламы математика задача 25 7 и 8 вариантСкачать

Окружность проходит через вершины C и D прямоугольной трапеции ABCD (угол C = углу D = 90 градусам)?

Окружность проходит через вершины C и D прямоугольной трапеции ABCD (угол C = углу D = 90 градусам).

Найти радиус окружности, если известно, что окружность касается прямой AB в точке B и длины боковых сторон трапеции равны 4 и 5.

Вопрос Окружность проходит через вершину А прямоугольника ABCD и касается сторон BC и CD в точках М и Nсоответственно?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

1) Пусть ABCD — трапеция, AD║AC — основания, ∠A = 85°, ∠D = 5°, K, L, M, N — середины сторон, KL = 11, NM = 1. 2) Продолжим стороны AB и CD до пересечения в точке Е. ΔAED — прямоугольный, так как∠Е = 180° — (85° + 5°) = 180° — 90° = 90°. ЕМ — меди..

Пусть дана трапеция АВСД, где КЕ = 1 середина ВС и МР = 11 середина боковых сторон АВ и СД. Продолжим боковые стороны до пересечения в точке Т, тогда угол АТД = 90 градусам. Обозначим половину ВС через х , а половину АД чрез у, тогда получим систем..

Вы можете конкретно написать задание? 1и2 это углы? Тем более как они могут иметь уголы если они параллельны? Есть ли секущая с? Без нее никак.

30 + 90 = 120° это угол один 90 — 30 = 60° это угол четыре или три.

Смотри рисунок, обозначения понятны. Из треуг. ДЕС ДС / sinα = a / sin60 ДC = а * sinα / sin60 из треуг КВД ВД / sin(180 — (α + 60)) = a / sin60 ВД = а * sin(α + 60) / sin60 AB = BC = ДС + ВД = а * sinα / sin60 + а * sin(α + 60) / sin60 = а * (2sin..

P = 2 * 2 + 6 = 10 Периметр равен 10см.

Ответ : 3 Этот треугольник равнобедренный, и если провести высоту — треугольник разделится на 2 равных прямоугольных треугольника. Гипотенуза треугольников будет 3, а катет окажется 3, 5. Катеты прямоугольных треугольников всегда меньше гипотенузы.

Длина суммы векторов AO и BO равна стороне AD. Ответ 91.

R = S / p S — площадь ромба, p — его полупериметр (p = 2a, где a — сторона ромба). R = 24 / 12 = 2 p = 6 * 2 = 12.

Если площадь 24 то ее стороны равны 6 соответсвенно. Радиус может быть половина ее диагонали.

Видео:Окружность проходит через вершины  A  и  C  треугольника ABC ... ОГЭ, геометрия, часть 11Скачать

Окружность проходит через вершину с прямоугольника авсд

Окружность проходит через вершину С прямоугольника ABCD, касается стороны AB, пересекает сторону CD в точке M и касается стороны AD в точке K.

А) Докажите, что угол CKD равен углу KMD.

Б) Найдите сторону AB, зная, что AD = 18, DM = 4.

А) Угол KCD — вписанный в заданную окружность, значит, измеряется половиной градусной меры дуги KM. А угол MKD образован хордой KM этой же окружности и касательной KD к той же окружности, и он измеряется половиной градусной меры дуги KM, заключенной между хордой и касательной. Значит, ∠KCD = ∠MKD. Но эти два угла есть острые углы двух прямоугольных треугольников KCD и MKD. Тогда обязаны быть равными и другие острые углы названных треугольников, т. е. ∠CKD = ∠KMD, что и требовалась доказать.

Б) Из полученного равенства ∠CKD = ∠KMD следует подобие: ΔMKD

Пусть R — радиус заданной окружности, O — ее центр, F ∈ CM, OF ⊥ CM. Пусть E ∈ AB, OE ⊥ AB.

Соединим точки O и K, O и E отрезками , тогда OK = OE = R. Кроме того, OK ⊥ KD. OE || AK как два перпендикуляра к AB. По аналогичной причине Следовательно, AEOK — параллелограмм, откуда AE = OK = R. Но AE = AK как отрезки касательных к окружности, проведенных из точки А. Следовательно, AK = AE = R. В таком случае KD = 18 − R.

Рассмотрим OE и OF как два перпендикуляра, проведенные из одной и той же точки О к параллельным прямым AB и CD, лежат на одной прямой. Тогда AEFD — прямоугольник, откуда: FD = AE = R.

Пусть CD = x, тогда CM = CD − MD = x − 4.

Треугольник COM — равнобедренный, в нем OF — высота по построению, следовательно, OF — медиана.

Это — с одной стороны. С другой же стороны, CF = CD − FD = x − R. Значит,

Так как KD = 18 − R, то в соответствии с равенствами (*) и (**) будем иметь:

Значение R = 34 не подходит по смыслу задачи, так как KD = 18 − R > 0.

При R = 10: AB = CD = x = 2R − 4 = 20 − 4 = 16.

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б.	3
Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки.	2
Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Видео:ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать Окружность проходит через вершину с прямоугольника авсд БАЗА ЗАДАНИЙ *Задание № 16. Планиметрия с доказательством.* 1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D. а) Докажите, что ∠ABM =∠DBС = 30°. б) Найдите расстояние от центра прямоугольника до прямой CM, если BC = 9. 2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно. а) Докажите, что периметр треугольника AMN равен стороне квадрата. б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3? Ответ: б) 1:3 3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD. а) Докажите, что AB:BC = AP:PD. б) Найдите площадь треугольника COD, где O— центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 6, а BC = 6√2. Ответ: б) 18√3 4. В треугольнике ABC точки A ₁ , B ₁ , C ₁ — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°. а) Докажите, что точки A₁, B₁, C₁, H— лежат на одной окружности. б) Найдите A₁ H, если BC = 2√3. 5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно. а) Докажите, что прямые KM и BC параллельны. б) Пусть L— точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16. Ответ: б) √10 6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P. а) Докажите, что прямые PQ и BC параллельны. б) Известно, что sin ∠AOC=√15/4. Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA. Ответ: б) 1:4 7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L. а) Докажите, что CN:CM = LB:LA. б) Найдите MN, если LB:LA = 2:3, а радиус малой окружности равен √23. Ответ: б) 115/6 8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N. а) Докажите, что прямые MN и BO параллельны. б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM:MC = 1:3. 9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D. а) Докажите, что прямые AD и MC параллельны. б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12. 10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны. а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD. б) Пусть N— точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 18. 11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно. а) Докажите, что отрезки AM и MK равны. б) Найдите MK, если AB = 5, AC = 8. Ответ: б) 2,88 12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB. а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC. б) Найдите угол OHI, если ∠ABC = 55°. 13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый. а) Докажите, что треугольник PQW— прямоугольный. б) Найдите площадь четырёхугольника ABCD. 14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C ₁ , B ₁ соответственно. а) Докажите, что треугольник АВC подобен треугольнику AB ₁ C ₁ . б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А = 45°, B ₁ C ₁ =6 и площадь треугольника AB ₁ C ₁ в восемь раз меньше площади четырёхугольника BCB ₁ C _{1 .} 15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD. а) Докажите, что луч AC— биссектриса угла BAD. б) Найдите CD, если известны диагонали трапеции: AC = 15 и BD = 8,5. 16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота. а) Докажите, что прямые MH и NH перпендикулярны б) Пусть Р – точка пересечения прямых АС и NH, а Q – точка пересечения прямых ВС и MH. Найдите площадь треугольника PQM, если АН = 12 и ВН = 3. 17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M. а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности. б) Найдите sin ∠BMC если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности. Ответ: б) 0,65 18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно. а) Докажите, что прямые ЕН и АС параллельны. б) Найдите отношение ЕН:АС, если угол АВС равен 30. Ответ: б) 3:4 19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно. а) Докажите, что KC = (KL+KM-LM)/2 . б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60. Ответ: б) 5:2 20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD. а) Докажите, что четырёхугольник DQOH — параллелограмм. б) Найдите AD, если ∠BAD = 75° и BC =1. Ответ: б) 3 21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K. а) Докажите, что CKCE = ABCD. б) Найдите отношение CK к KE, если ∠ ECD = 15. Ответ: б) 2:1 22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L а) Докажите, что треугольники AML и BLC подобны. б) Найдите отношение площадей этих треугольников, если cos ∠BAC = 7/25. Ответ: б) 25:36 23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части. а) Докажите, что треугольник ABC равнобедренный. б) Найдите, в каком отношении высота этого треугольника делит сторону BC. Ответ: б) 5:4 24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P. а) Докажите, что прямые PM и QM перпендикулярны. б) Найдите PQ, если AM = 1, BM = 3, а Q – середина дуги MB. 25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K. а) Докажите, что отрезок BK втрое больше отрезка CK. б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23. 26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности. а) Прямая, проходящая через центр окружностей, пересекает основание AD в точке P. Докажите, что AP/PD = sin ∠D. б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1. 27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O. а) Докажите, что sin ∠AOD = sin ∠ BOS. б) Найдите площадь трапеции, если ∠ BAD = 90, а основания равны 5 и 7. 28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17. а) Докажите, что диагонали перпендикулярны. б) Найдите площадь трапеции. 🎬 Видео Геометрия Окружность проходит через вершины А и С треугольника АВС и пересекает его стороны АВ и ВССкачать Математика ОГЭ Задание 25 Первый признак подобияСкачать Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть I)Скачать №152. Через вершину В квадрата ABCD проведена прямая BF, перпендикулярная к его плоскости. НайдитеСкачать Стереометрия 10 класс. Часть 1 \| МатематикаСкачать Окружность проходит через вершины А, В и D параллелограммаСкачать ЗАДАЧА - ПРОСТО ОТДЫХ КАКОЙ-ТО!Скачать Поделиться или сохранить к себе: Search for: Прямые 21 билет по геометрии содержит 3 вопроса по теме параллельные прямые 19 1034 Вектор Вектор степеней и полустепеней вершин 1019 Окружность Цветок из окружностей циркулем поэтапно 1016 Вектор Герб минцифры россии в векторе 1021 Вектор Вектор механического момента действующего на контур с током Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности О сайте \| \| © 2024 Курс школьной геометрии.

Критерии оценивания выполнения задания

Баллы

Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б.

Получен обоснованный ответ в пункте б.

Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки.

Имеется верное доказательство утверждения пункта а.

При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки.

Видео:ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

Окружность проходит через вершину с прямоугольника авсд

БАЗА ЗАДАНИЙ

Задание № 16. Планиметрия с доказательством.

1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.
а) Докажите, что ∠ABM =∠DBС = 30°.
б) Найдите расстояние от центра прямоугольника до прямой CM, если BC = 9.

2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
Ответ: б) 1:3

3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.
а) Докажите, что AB:BC = AP:PD.
б) Найдите площадь треугольника COD, где O— центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 6, а BC = 6√2.
Ответ: б) 18√3

4. В треугольнике ABC точки A ₁ , B ₁ , C ₁ — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°.
а) Докажите, что точки A₁, B₁, C₁, H— лежат на одной окружности.
б) Найдите A₁ H, если BC = 2√3.

5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L— точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
Ответ: б) √10

6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что sin ∠AOC=√15/4. Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.
Ответ: б) 1:4

7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L.
а) Докажите, что CN:CM = LB:LA.
б) Найдите MN, если LB:LA = 2:3, а радиус малой окружности равен √23.
Ответ: б) 115/6

8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM:MC = 1:3.

9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.

10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть N— точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 18.

11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB = 5, AC = 8.
Ответ: б) 2,88

12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB.
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OHI, если ∠ABC = 55°.

13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый.
а) Докажите, что треугольник PQW— прямоугольный.
б) Найдите площадь четырёхугольника ABCD.

14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C ₁ , B ₁ соответственно.
а) Докажите, что треугольник АВC подобен треугольнику AB ₁ C ₁ .
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А = 45°, B ₁ C ₁ =6 и площадь треугольника AB ₁ C ₁ в восемь раз меньше площади четырёхугольника BCB ₁ C _{1 .}

15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что луч AC— биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC = 15 и BD = 8,5.

16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота.
а) Докажите, что прямые MH и NH перпендикулярны
б) Пусть Р – точка пересечения прямых АС и NH, а Q – точка пересечения прямых ВС и MH. Найдите площадь треугольника PQM, если АН = 12 и ВН = 3.

17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin ∠BMC если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
Ответ: б) 0,65

18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны.
б) Найдите отношение ЕН:АС, если угол АВС равен 30.
Ответ: б) 3:4

19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно.
а) Докажите, что KC = (KL+KM-LM)/2 .

б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60.
Ответ: б) 5:2

20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC =1.
Ответ: б) 3

21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K.
а) Докажите, что CK*CE = AB*CD.
б) Найдите отношение CK к KE, если ∠ ECD = 15.
Ответ: б) 2:1

22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если cos ∠BAC = 7/25.
Ответ: б) 25:36

23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону BC.
Ответ: б) 5:4

24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P.
а) Докажите, что прямые PM и QM перпендикулярны.
б) Найдите PQ, если AM = 1, BM = 3, а Q – середина дуги MB.

25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23.

26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центр окружностей, пересекает основание AD в точке P. Докажите, что AP/PD = sin ∠D.
б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.

27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O.
а) Докажите, что sin ∠AOD = sin ∠ BOS.
б) Найдите площадь трапеции, если ∠ BAD = 90, а основания равны 5 и 7.

28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.