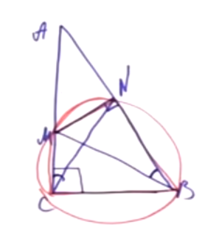
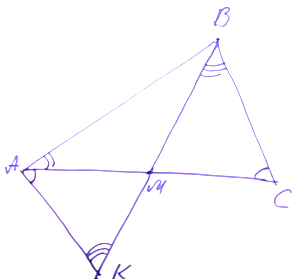
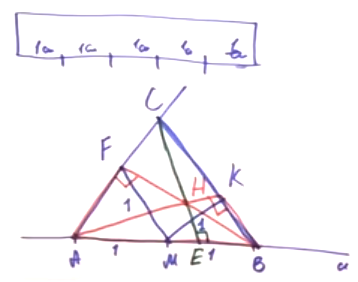
Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 18 и BN = 17.
а) Проведём медиану AE к основанию BC, поскольку треугольник ABC — равнобедренный, медиана AE является биссектрисой и высотой. Проведём MK, заметим, что ∠BKM = 90°, так как он вписанный и опирается на диаметр окружности. Поэтому MK перпендикуляр к ВС. Тогда MK — средняя линия AEС, и тогда КС = EК. Поскольку CE = 2CK, имеем: BK = 3CK, что и требовалось доказать.
б) Заметим, что ∠BKM = ∠BNM = 90°, так как эти углы вписанные и опираются на диаметр. Тогда (*), причём:
Подставляя полученные соотношения в (*), получаем:
Тогда
Приведём другое решение пункта б).
Пусть Тогда
и пусть
тогда
По свойству секущих имеем:
Приведём третье решение пункта б).
Пусть угол при вершине A треугольника ABC равен 2α, AB = x. Тогда из прямоугольного треугольника ANM находим: Из треугольника MKC:
таким образом, получаем уравнение:
Из последнего уравнения получаем те же ответы, что и в предыдущем решении x = 16 (постороннее решение) или x = 18.
Приведём еще одно решение пункта б).
Рассмотрим прямоугольный треугольник Если AB = x, то
С другой стороны из треугольника ABC по теореме косинусов имеем
Составим уравнение:
Последнее уравнение уже дважды решено выше.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
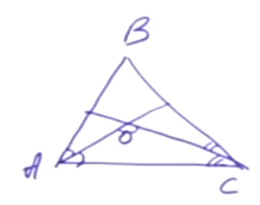
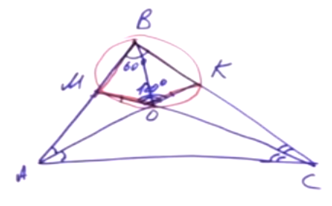
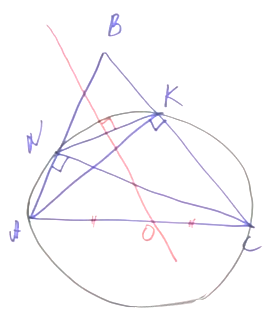
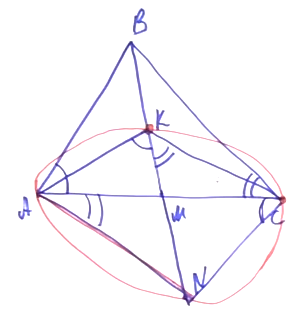
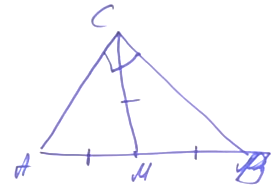
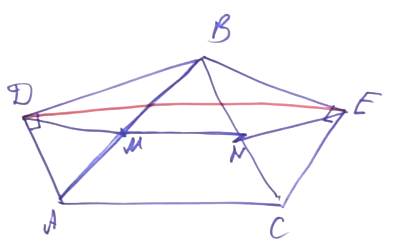
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Окружность построенная на медиане вмОкружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K. а) Докажите, что отрезок BK втрое больше отрезка CK. б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23. а) Проведём медиану AE к основанию BC, поскольку треугольник ABC — равнобедренный, медиана AE является биссектрисой и высотой. Проведём MK, заметим, что ∠BKM = 90°, так как он вписанный и опирается на диаметр окружности. Поэтому MK перпендикуляр к ВС. Тогда MK — средняя линия AEС, и тогда КС = EК. Поскольку CE = 2CK, имеем: BK = 3CK, что и требовалось доказать. б) Заметим, что ∠BKM = ∠BNM = 90°, так как эти углы вписанные и опираются на диаметр. Тогда Подставляя полученные соотношения в (*), получаем: Тогда Ответ: б) Видео:Окружность, построенная на стороне треугольника как на диаметреСкачать  Осваиваем простые приемы решения геометрических задачИдея IЕсли в четырехугольнике суммы противоположных углов равны 180°, то вокруг этого четырехугольника можно описать окружность. Задача. Дан прямоугольный треугольник ABC. На катете АС выбрана произвольная точка М. Из точки М опущен перпендикуляр MN на гипотенузу. Докажите, что углы MCN и MBN равны. Решение. Угол MNB — прямой. По условию, треугольник ABC прямоугольный, значит, есть еще один прямой угол. Обратим внимание на четырехугольник MNBC: в нем есть два противолежащих прямых угла, их сумма равна 180°. Следовательно, вокруг четырехугольника MNBC можно описать окружность. Углы, равенство которых нужно доказать, опираются на одну дугу MN и являются вписанными. Два вписанных угла опираются на одну и ту же дугу, значит, они равны. Идея IIЕсли известен угол треугольника, можно найти угол между биссектрисами, обращенными в сторону этого угла. Задача. Дан треугольник ABC. Проведены биссектрисы углов A и С, они пересекаются в точке O. Найдите угол AOC (т.е. есть угол между биссектрисами). Решение. Известно, что ∠ABC = ∠В. Эту задачу легко решить с помощью теоремы суммы углов треугольников. ∠A + ∠C = 180° – ∠B. Суммы половинок углов А и С равны 90° – ½ ∠B. Тогда ∠AOC = 90° + ½ ∠B. Совмещение идей I и II Некоторые задачи находятся как бы на пересечении нескольких идей решения. Задача. Дан треугольник ABC. Известно, что угол В равен 60°. Проведены биссектрисы углов: АК и СМ, они пересекаются в точке О. Докажите, что отрезок ОМ равен отрезку ОК. Решение. Найдем угол АОС по формуле 90° + ½ ∠B. ∠В = 120°. Обращаем внимание на четырехугольник МВКО. В нем сумма противоположных углов равна 180°, значит, вокруг него можно описать окружность. О — точка пересечения биссектрис треугольника АВС. Следовательно, луч ВО делит угол АВС пополам. ∠МВО = ∠ОВК. Данные углы являются вписанными, значит, равны и дуги, на которые они опираются. Дуга МО равна дуге ОК. Известно, что равные дуги стягивают равные хорды. Хорда ОМ равна хорде ОК. Идея IIIЕсли из двух точек, лежащих в одной полуплоскости, отрезок между двумя другими точками виден под одним и тем же углом, то эти 4 точки лежат на одной окружности. Задача. Дан остроугольный треугольник АВС. Проведены две высоты: АК и СN. Докажите, что серединный перпендикуляр отрезка NK пересекает отрезок АС в середине (точка О является серединой отрезка АС). Решение. ∠ANC = ∠AKC. Мы можем нарисовать окружность вокруг четырехугольника ANKC. Отрезок NK является в этой окружности хордой, а АС — диаметром, поскольку он виден из точек N и K под прямым углом. Серединный перпендикуляр проведен к хорде, он содержит диаметр окружности. Два диаметра пересекаются в центре окружности. О — это центр окружности. АО и ОС — это диаметры. Следовательно, АО = ОС. Идея IVЕсли в треугольнике продлить медиану и построить параллелограмм, можно извлечь много дополнительных данных для решения задачи. Задача. Дан треугольник АВС и его медиана ВМ. Известно, что ВМ в два раза меньше стороны АВ. Докажите, что угол МВС равен сумме ∠А + ∠С. Решение. Воспользуемся построением параллелограмма. Проведем МК. BM = ½ ВК. Следовательно, АВ = ВК. В этом случае треугольник АВК является равнобедренным. В равнобедренном треугольнике углы при основании равны, значит, ∠ВАК = ∠ВКА. ∠КАМ = ∠С. ∠АКВ = ∠СВК. Из этого мы получаем необходимое равенство. Совмещение идей III и IV Задача. Дан треугольник АВС, в котором проведена медиана ВМ. На медиане ВМ выбрана точка К так, что ∠ВАС = ∠АКМ. Докажите, что ∠ АСВ = ∠МКС. Решение. Продлим медиану на ее длину и получим точку N. BM = MN. ABCN — параллелограмм. ∠BAC = ∠ACN. Из точек К и С, лежащих по одну сторону от прямой, видим отрезок AN под одним и тем же углом. Вокруг четырехугольника AKCN описываем окружность. Поскольку ABCN — параллелограмм, ∠NAC = ∠BCA. Но углы NAC и NKC являются вписанными, опирающимися на одну дугу. Следовательно, ∠NAC = ∠NKC. Так мы доказали, что ∠МКС = ∠МСВ. Идея VЕсли в прямоугольном треугольнике АВС проведена медиана из вершины прямого угла, то медиана СМ будет равняться половине гипотенузы АВ. То есть СМ = АМ = МВ. Задача. Дан треугольник АВС. На внешние стороны построены два прямоугольных треугольника: ADB и BEC. Докажите что отрезок DE, соединяющий вершины прямых улов, не больше полпериметра треугольника АВС. Решение. Проведем медианы через точки M и N (середины сторон АВ и ВС). Соединим точки, образовав четырехугольник DENM. Звено ломаной DE не превосходит сумму длин отрезков DM + MN + NE. DE ≤ DM + MN + NE = ½ АВ + ½ АС + ½ ВС. Следовательно, DE ≤ ½ Равс Факт, обратный данному. Если в треугольнике АВС медиана СМ равна половине стороны АВ, значит, АСВ = 90°. Т.е. если в треугольнике медиана равна половине стороны, к которой она проведена, то этот треугольник является прямоугольным. Рассмотрим эту идею, продемонстрировав также, как только с помощью линейки можно решить задачу на построение перпендикуляра к данной прямой. Возьмем линейку с ценой деления 1 см. Отложим отрезки: точки А, М и В, так, что АМ = МВ = 1 см. Развернув линейку, поставим точку F (MF = 1 см) и точку К (МК = 1 см). С помощью линейки соединим A и F, B и K и продлим прямые до пересечения в точке С. На рисунке виден треугольник АFВ. FM в нем медиана, равняющаяся половинке стороны. Следовательно, угол F — прямой. Таким же свойством обладает треугольник АКВ. В треугольнике АСВ отрезки АК и ВF являются высотами. Значит, точка H в пересечении высот является центром треугольника. Если соединить СН и продлить в СЕ, это тоже будет высота треугольника АВС. Следовательно, СЕ перпендикулярно АВ. Так, только с помощью линейки мы провели прямую, перпендикулярную данной. В учебниках авторства Мерзляка А.Г., Полонского В.Б. и Якира М.С. образцовые задачи, демонстрирующие ту или иную идею решения, выделены и обозначены изображением ключа. 🎥 ВидеоТреугольник. На медианах как на диаметрах построены окружности. Задание 16 (34)Скачать  11.49.1. Планиметрия. Гордин Р.К.Скачать  Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать  Решаем Задание 16 ЕГЭ по математикеСкачать  Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать  7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать  На катете ML прямоугольного треугольника KLM как на диаметре построена окружностьСкачать  Построение медианы в треугольникеСкачать  Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать  Медиана, высота и биссектриса треугольника. Центроид, инцентр, ортоцентр. Геометрия 7 класс.Скачать  #31. Регион ВсОШ 2023, 11.5Скачать  Все свойства медианы в одной задаче.Скачать  окружности огэ по математике 2023 / маттаймСкачать  Планиметрия_Треугольник_02Скачать  Формулы для медианы треугольникаСкачать  Все факты о медиане треугольника для ЕГЭСкачать  Планиметрия. Окружность. Касательная. Медиана треугольника. Задание 16 (39)Скачать  Как построить окружность, описанную около треугольника, в программе ГЕОГЕБРАСкачать  |