Окружность под углом как чертить

Из геометрии известно, что круг можно рассматривать как правильный многоугольник с большим количеством сторон. Следовательно, изометрическое изображение круга можно строить так же, описывая вокруг него квадрат (рис. 155, а). Точки касания А, В, С и D будут находиться на средине сторон квадрата и легко могут быть нанесены на аксонометрическое изображение (рис. 155, б). Промежуточные точки Е’, F’ и другие находим с помощью их координат. Изометрической проекцией круга является эллипс; его большая ось EG расположена под углом 60° к горизонту по большой диагонали ромба, а малая ось — под углом 30° по малой диагонали ромба.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451018_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Аксонометрические изображения круга чаще строят, проводя оси х и у через центр окружности (рис. 156, а); при этом отпадает надобность в построениях квадрата и ромба. Выбрав точку О’, проводим через нее оси х’ и у’ (рис. 156, б), откладываем на осях величины, равные радиусу окружности, получаем точки А’, В’, С и D’. Другие точки находим с помощью их координат; построение точки Е показано двойными тонкими линиями. Два координатных отрезка для точки Е составляют так называемую координатную ломаную, которая будет в дальнейшем широко применяться при построении точек, расположенных в пространстве. Большая ось эллипса E’G’ для круга, лежащего в плоскости х’О’у’, расположена горизонтально, а малая ось — вертикально.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451012_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

В начертательной геометрии доказывается, что отношение осей эллипса, являющегося изображением окружности, в прямоугольной изометрии равняется 0,58, т. е. если большую ось эллипса d принять за единицу, то малая ось будет равна 0,58d. Это положение иллюстрируем так: расположим плоскость квадрата, в который вписана окружность, параллельно плоскости П₂ (рис. 157, а); повернем квадрат вокруг его горизонтальной диагонали на угол, равный 54° 30′ (рис. 157, б); спроецируем квадрат и окружность на плоскость, параллельную горизонтальной диагонали квадрата (рис. 157, е). Диагональ ромба и горизонтальный диаметр окружности спроецируются при этом в действительную величину, стороны ромба изобразятся прямыми, составляющими =0,82 от величины d; наклоненные диагональ и диаметр окружности спроецируются с искажением и составят 0,58 от своей действительной величины, поскольку sin 35°30′ = 0,58.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451023_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Изображение окружности на рис. 157, в является натуральным. Чтобы перейти к «приведенному» изображению, которое, как известно, увеличено в 1,22 раза, умножим все три величины на указанное количество раз. Получим: сторона ромба 0,82dxl,22 = 1,004d = d; большая ось эллипса dx 1,22 = 1,22d; малая ось эллипса 0,58dx1,22= 0,71d.

Зная эти зависимости, мы можем по заданному диаметру круга быстро найти размеры большой и малой осей эллипса, являющегося изометрической проекцией окружности. Пусть требуется построить прямоугольную изометрию круга, диаметр окружности которого равен 50 мм. Определяем размеры большой и малой осей эллипса: большая ось А’В’ равна 50х X 1,22 = 61 мм, малая ось CD’ равна 50’х0,71=35 мм. Строим по этим размерам оси эллипса на чертеже (рис. 158, а).

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451055_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

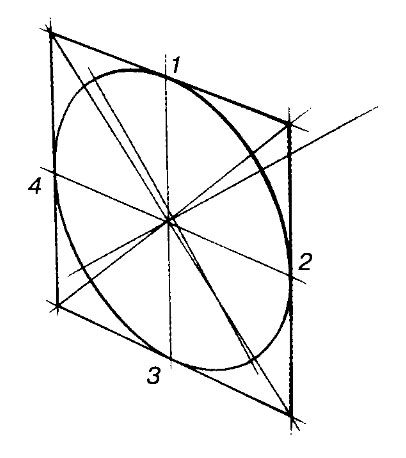
Из геометрического черчения известно (см. рис. 47), что по осям эллипса можно построить его кривую. Практически эллипс в изометрии обычно заменяют овалом, который строят следующим образом (рис. 158, б). На большой А’В’ и малой CD’ осях строим две окружности; они пересекают продолжение малой оси в точках 1 и 2, а большую ось — в точках 3 и 4; эти точки являются центрами для дуг овала; используя их, вычерчиваем овал с радиусами r = О’В’—О’С и R = CD’ + г. Точку сопряжения дуг радиусов R и г находим, соединяя точки 1 и 4 прямой и продолжая эту прямую до пересечения с дугами в точке 5.

В прямоугольной изометрии все три эллипса одинаковы по форме, равны друг другу и лишь расположены различно. В отличие от этого в прямоугольной диметрии имеются две различные формы эллипса: одна для плоскости х’О’z’, а другая — для плоскостей х’О’у’ и z’O’y’.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451008_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Пусть требуется построить прямоугольную диметрию окружности, лежащей в плоскости хОz (рис. 159, а). Описываем вокруг окружности квадрат и проводим его диагонали. Отмечаем точки пересечения диагоналей с окружностью и координатные отрезки, нужные для построения точек Е, F и др. Строим квадрат в прямоугольной диметрии (рис. 159, б), проводим его средние линии А’С и B’D’ и диагонали. Пользуясь координатными отрезками (помечены на чертежах тонкими двойными линиями), находим точки Е’, F’, G’ и H’. Большая ось эллипса F’G’ в прямоугольной диметрии будет равна l,06d, малая ось Е’Н’ будет равна 0,95d (отношение 9 : 10). Полученные восемь точек соединяем от руки, а затем обводим по лекалу. Если требуется более точное построение, то находят с помощью координатных ломаных еще ряд промежуточных точек.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451062_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

В практике эллипс нередко заменяют овалом (рис. 160, а). Центры дуг для построения овала находим так: строим ромб, его средние линии и диагонали, Из центра О’ радиусом r=d/7 проводим вспомогательную окружность.

Она пересекает малую диагональ ромба в точках 1 и 2; используем эти центры для проведения дуг А’В’ и CD’. Соединяем точки А’ и I, С и 2; эти линии пересекают большую диагональ в точках 3 и 4. Пользуясь этими центрами, проводим дуги A’D’ и В’С. При этом способе также не требуется откладывать размеры большой и малой осей; они получаются сами собой при проведении дуг.

Если требуется построить прямоугольную диметрию окружности, лежащей в плоскости х’О’у’, то на осях х’ и у’ строим параллелограмм и намечаем средние точки его сторон (рис. 160, б). Затем через точку О’ проводим горизонтальную прямую — направление большой оси эллипса. Откладываем на этой прямой размер большой оси эллипса, равный 1,06d. Перпендикулярно к ней проводим малую ось эллипса, размер которой равен 0,35d (отношение 3 : 10). Таким путем получаем восемь точек, принадлежащих эллипсу. В практике избегают построения параллелограмма и строят вместо эллипса овал по его осям А’В’ и CD’ (рис. 160, в). Последовательность построения такая: от центра О’ на продолжении малой оси эллипса откладываем величину большой оси А’В’; получаем точку 1 — центр верхней дуги радиуса R. Тем же радиусом из точки 2 (не показана на чертеже) проводим нижнюю дугу овала. Слева и справа овал дочерчиваем кривыми радиуса r, величину которого принимаем равным r=O’C’/2 Центры 3 и 4 находим, делая засечки дугами r из точек А’ и В’. Точку сопряжения 5 находим, соединяя прямой точки I и 4 и продолжая эту прямую до пересечения с дугой.

Окружность, находящаяся в плоскости, параллельной фронтальной плоскости проекций, проецируется на нее во фронтальной изометрической проекции в виде окружности (рис. 161, а), а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, — в эллипсы, большие оси которых наклонены к осям х’ и z’ под углами 22° 30′. Большие оси эллипсов равны 1,3 диаметра окружности, малые — 0,54 диаметра окружности.

Пусть требуется построить во фронтальной изометрии окружность диаметра 40 мм, находящуюся в плоскости х’О’у’. Определяем большую и малую оси эллипса. Большая ось А’В’ = 1,3d = 1,3 40 = 52 мм, малая ось CD’ = 0,54d = 0,54-40 = 21,6 мм. Овал, заменяющий собой эллипс, удобно строить из четырех центров радиусами, равными R = 1,3d и r = = 0,16d (рис. 161, б). В нашем примере R — 52 мм, г = 0,16d = 6,4 мм. Точка 5 — точка сопряжения.

Окружность, находящаяся в плоскости, параллельной горизонтальной плоскости проекций, проецируется на нее в горизонтальной изометрической проекции в виде окружности (рис. 161, б), а окружности, находящиеся в плоскостях, параллельных фронтальной и профильной плоскостям проекций, — в эллипсы. Большая ось эллипса, параллельного плоскости ?’?’z’, наклонена к оси z’ под углом 15° и равна l,37d; малая ось равна 0,37d. Большая ось эллипса, параллельного плоскости z’О’у’, наклонена к оси у’ под углом 30° и равна 1,22d; малая ось равна 0,71d (так же, как в прямоугольной изометрической проекции).

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Сопряжения

В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Ниже будут рассмотрены основные типы сопряжений.

Видео:Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение углов (Сопряжение пересекающихся прямых)

Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)

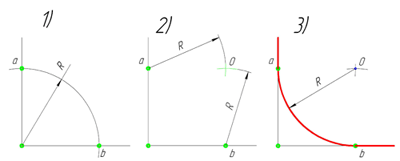
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.

Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)

Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

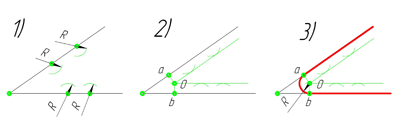
Сопряжение параллельных прямых линий

Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение окружностей(дуг) с прямой линией

Внешнее сопряжение дуги и прямой линии

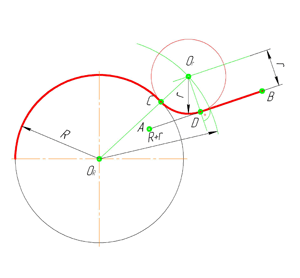
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности O R радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой О r .

Из центра сопряжения, точки О r , опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности О R и центр сопряжения О r линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.

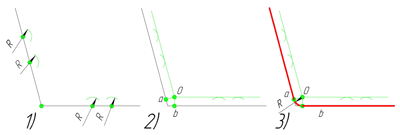
Внутреннее сопряжение прямой линии с дугой

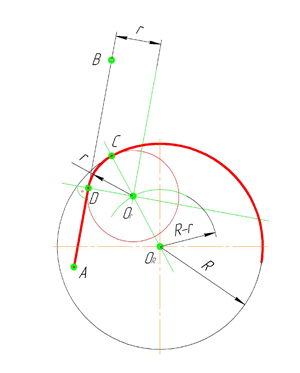
По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности O R радиусом R-r. Точка О r , полученная на пересечении прямой и дуги, и будет центром сопряжения.

Из центра сопряжения(точка О r ) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности О R прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки О r , центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.

Видео:1 2 4 сопряжение окружностейСкачать

Сопряжение окружностей (дуг)

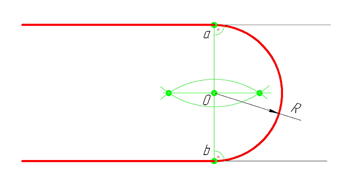
Внешнее сопряжение дуг окружностей

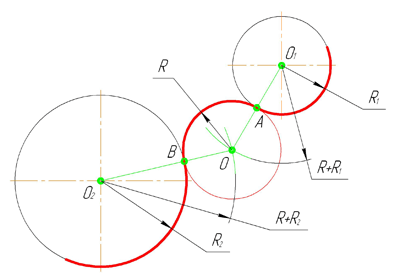
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Внутреннее сопряжение дуг окружностей

Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

Смешанное сопряжение дуг окружностей

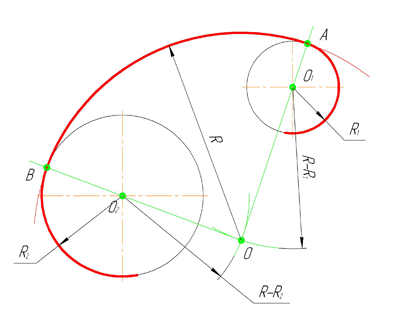
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

Видео:Построение угла, равного данному. 7 класс.Скачать

ИЗОБРАЖЕНИЕ ОКРУЖНОСТИ В ПЕРСПЕКТИВЕ.

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Перспектива окружности в горизонтальной плоскости.

Множество предметов, находящихся вокруг нас, имеют формы,

очертанием которых является окружность.

Чаще всего эта окружность находится в горизонтальной плоскости: это могут быть края чашки, стоящей на столе или табуретка с круглым сидением.

Если такая окружность находится на уровне наших глаз, на линии горизонта, мы видим ее как прямую линию.

Если мы смотрим на окружность сверху, то мы видим ее без искажений, как окружность.

Во всех остальных случаях, когда окружность располагается в горизонтальной плоскости, мы видим ее как эллипс.*

То есть, как лекальную кривую, симметричную относительно двух взаимно перпендикулярных осей.

При чем, одна из этих осей ВСЕГДА строго вертикальна, а другая, соответственно, горизонтальна.

*Строго говоря, изображение окружности в перспективе не является эллипсом, так как дальняя от нас его часть чуть меньше, чем ближняя. И, соответственно, он не симметричен относительно горизонтальной оси.

Соотношение между длинами осей эллипса называют раскрытием.

Грубо говоря, чем больше эллипс похож на круг, тем более он раскрытый.

В изображении эллипсов в горизонтальной плоскости есть два основных правила:

1. Чем дальше находится эллипс от линии горизонта, тем более раскрытым мы его картинка
2. Дальняя часть эллипса ЧУТЬ меньше, чем ближняя.

Легко понять, почему это так , построив в перспективе окружность вписанную в квадрат.

Видео:ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать

Упражнение 1.

Постройте окружность тем же способом, с той же точкой схода, но выше линии горизонта. Выделите более толстой линией ее передний край.

ОБРАТИТЕ ВНИМАНИЕ что в рисунке окружности, лежащие в горизонтальной плоскости мы НЕ строим с помощью описанного квадрата. Так как этот даёт искажения, если точка схода для квадрата не лежит на вертикальной оси эллипса.

Мы проводим две оси эллипса и задаем степень раскрытости на глаз, но учитываем положение эллипса относительно линии горизонта и других эллипсов.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Упражнение 2.

На рисунках изображена последовательность построения цилиндра и конуса.

Нарисуйте цилиндры и конусы выше и ниже линии горизонта . Раскрытие эллипсов задаём на глаз. Окружность в квадрат не вписываем.

Видео:Построение пятиугольника циркулемСкачать

Перспектива окружности в вертикальной или наклонной плоскости.

С окружностями в вертикальной плоскости нам приходится иметь дело достаточно часто. Например, рисуя арки в архитектуре.

Самый простой случай — когда окружность находится в плоскости параллельной картинной. Тогда мы видим ее без искажений.

View of the Tiber with the Castel Sant’Angelo
Bernardo Bellotto1743/1744

Если окружность находится под углом к картине, для построений мы также используем описанный квадрат. Этот способ применяется как в черчение, так и в рисунке, так как на глаз нарисовать окружность в таком ракурсе очень сложно .

В этом курсе мы только знакомимся со способом построения окружности в вертикальной плоскости. Но если у вас есть желание, подробно об этом можно прочитать в учебнике Осмоловской (ст. 26) или, в упрощенном виде у Шарова и Барщ.

Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Перспективные зарисовки с натуры.

Мы закончили блок теории построений. Теперь начинаем работать с натуры.

На этом этапе важно осознать, что рисунок — не черчение. В рисунке мы не пользуемся линейкой, редко строим точки схода на дополнительном листе. Наша задача, зная, какие построения применялись бы для перспективного чертежа, сделать минимум из них на глаз так, чтобы в результате получилось убедительное изображение, соответствующее основным правилам перспективы.

Рисование с фотографии.

Я вас очень прошу, по крайней мере на начальном этапе не срисовывать с фотографии, даже называя это рисованием с референсов.

Рисуя с фото вы НЕ развиваете пространственное воображение и умение на плоскости изображать объем. Вы только учитесь копировать с одного листа на другой пятна тона. Это, конечно, тоже полезный навык но для хорошего рисунка его не достаточно.

Постановка натуры.

Правильная постановка натуры помогает избежать многих ошибок в рисунке и делает работу легче и приятнее.

Поэтому я очень прошу вас уделить этому внимание.

• Организуйте рабочее место так, чтобы смотреть на натуру все время с одной точки зрения. Если вы работаете в несколько сеансов, запомните, где вы стояли или сидели относительно натуры. Чтобы не оказалось так, что половина предметов на работе у вас сделана с одной точки зрения, а половина — с другой.

• Не садитесь слишком близко или слишком далеко от натуры. Между вами и натурой должно укладываться примерно два ее размера.

• В начале обучения, старайтесь ставить предметы на контрастный фон, чтобы их очертания хорошо читались.

• В начале обучения, не ставьте предметы против света или с несколькими источниками света. Старайтесь чтобы освещение было сбоку и форма предметов хорошо читалась.

• Отходите от рисунка или переворачивание его кверх ногами. Так вы увидите ошибки. Ещё можно смотреть на работу в зеркало.

Видео:КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

Рисунок с натуры коробки или книжки.

• Задаем положение переднего вертикального ребра и определяем, под каким углом к горизонтали мы видим нижние ребра.

• Определяем пропорции.Смысл рисования с натуры в том, чтобы она была передана точно. Эту задачу не решить без соблюдения пропорций. То есть отношений разных размеров объектов друг к другу. Если вы сделаете лицо портретируемого в два раза шире, чем на самом деле, вряд ли он вас за это поблагодарит. Для измерения пропорций есть достаточно простые приемы. О них я рассказываю на этом видео.

Видео:Построение угла равного данномуСкачать

Упражнение 4

Нарисуйте с натуры предмет с прямыми ребрами ( книжку, коробку и т. п.)

Мы НЕ рисуем с фото, мы НЕ копируем рисунок, разобранный выше.

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Упражнение 5

Нарисуйте два предмета с прямыми ребрами, один из которых стоит на другом.

Видео:Геометрия - Построение шестиугольникаСкачать

РИСУНОК С НАТУРЫ КРУЖКИ.

Для постановки нужно выбрать кружку простой цилиндрической формы, с ручкой. Саму кружку мы видим без сокращений, поэтому отношение высоты и ширины можно измерить, приложив карандаш непосредственно к натуре.

• Начинаем с построения цилиндра. Помним, что чем дальше эллипс от линии горизонта, тем более он раскрыт.

• Строим толщину стенок кружки.

• Строим ручку: начинаем с мест крепления ручки, обратите внимание, что они находятся на одной вертикальной оси.

• Строим ось ручки. обратите внимание, что она лежит в плоскости, проходящей через центр цилиндра.

• Строим внешнюю, внутреннюю и боковую поверхности ручки.

Видео:Как начертить овал во фронтальной плоскостиСкачать

Упражнение 6

Нарисуйте кружку с натуры.

Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Упражнение 7.

Нарисуйте ту же кружку в другом ракурсе по представлению(не глядя на натуру)

📽️ Видео

Построение биссектрисы угла. 7 класс.Скачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Построение 8 угольника циркулемСкачать