Окружность с центром в точке O высекает на всех сторонах трапеции ABCD равные хорды.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной и той же точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB в точках K и L так, что AK = 11, KL = 10, LB = 4.
a) Расстояние от центра окружности до хорд одинаковой длины равны. Следовательно, точка O равноудалена от прямых AB, BC, CD и AD. Значит, она лежит на биссектрисе каждого из углов трапеции.
б) Опустим из точки O перпендикуляры OU, OV и OW на стороны AD, AB и BC соответственно. Тогда 
UW — высота трапеции, а точка V — середина отрезка KL. Значит,
Пусть BH — высота трапеции. В прямоугольном треугольнике ABH имеем: 
Приведем решение Максима Волкова.
Опустим из точки O перпендикуляры OU, OV и OW на стороны AD, AB и BC соответственно. Тогда 
UW — высота трапеции, а точка V — середина отрезка KL. Тогда
Проведем отрезки АО и ОВ. Заметим, что треугольник AOB прямоугольный, так как АО и ВО — биссектрисы углов трапеции при боковой стороне. Тогда по свойству высоты прямоугольного треугольника находим:
Следовательно, для высоты трапеции получаем:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Аналоги к заданию № 520805: 520917 520855 520881 Все
Равные хорды
Выясним, какими свойствами обладают равные хорды и равные дуги.
Равные хорды равноудалены от центра окружности.
Дано : окр. (O;R), AB и CD — хорды,
Соединим центр окружности с концами хорд.
I. Рассмотрим треугольники AOB и COD.
1) AB=CD (по условию)
2) OA=OB=OC=OD (как радиусы).
Следовательно, ∆AOB = ∆COD (по трём сторонам).
Из равенства треугольников следует равенство соответствующих углов: ∠A=∠C.
II. Рассмотрим прямоугольные треугольники AOF и COK.
2) ∠A=∠C (по доказанному).
Из равенства треугольников следует равенство соответствующих сторон: OF=OK.
Что и требовалось доказать .
Если хорды равноудалены от центра окружности, то они равны.
Дано: окр. (O;R), AB и CD — хорды,
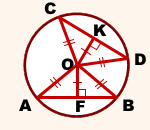
Соединим центр окружности с концами хорд.
I. Рассмотрим прямоугольные треугольники OKD и OFB.
1)OF=OK (по условию)
2)OD=OB (как радиусы).
Из равенства треугольников следует равенство соответствующих сторон:
II. Рассмотрим треугольники AOB и COD.
Так как OA=OB=OC=OD (как радиусы), треугольники AOB и COD — равнобедренные с основаниями AB и CD и высотами OK и OF соответственно.
По свойству равнобедренного треугольника, OK и OF — медианы, то есть AF=BF, CK=DK, откуда AB=CD.
Что и требовалось доказать.
Равные хорды стягивают равные дуги.
Дано : окр. (O;R), AB и CD — хорды, AB=CD,
Соединим центр окружности с концами хорд.
Рассмотрим треугольники AOB и COD
1) AB=CD (по условию)
2) OA=OB=OC=OD (как радиусы).
Следовательно, ∆AOB = ∆COD (по трём сторонам).
Из равенства треугольников следует равенство соответствующих углов: ∠AOB=∠COD.
Значит и дуги, на которые опираются эти центральные углы, также равны: ∪AB=∪CD
Что и требовалось доказать .
Хорды, стягивающие равны дуги, равны.
Дано: окр. (O;R), AB и CD — хорды,
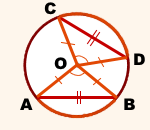
Соединим центр окружности с концами хорд.
Рассмотрим треугольники AOB и COD
Так как OA=OB=OC=OD (как радиусы), то треугольники AOB и COD — равнобедренные с основаниями AB и CD соответственно.
Так как ∪AB=∪CD (по условию), то ∠AOB=∠COD.
Из равенства треугольников следует равенство соответствующих сторон: AB=CD.
Окружность отсекает на всех сторонах треугольника равные хорды
Задание 16. Окружность с центром в точке О пересекает каждую из сторон трапеции ABCD в двух точках. Четыре получившиеся хорды окружности равны.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону АВ в точках K и L так, что АК = 13, KL = 6, LB = 1.
а) ABCD – трапеция, BL – биссектриса, следовательно, 
. Так как AD параллельна BC, то 
и 
, следовательно, угол ALB=90° и BL перпендикуляра AC.
Аналогично доказывается, что CL перпендикулярна BD. Получаем, что диагонали BD и AC перпендикулярны и в то же время являются биссектрисами углов. Следовательно, трапеция ABCD – это ромб, а у ромба биссектрисы всех углов пересекаются в одной точке.
б) Задача сводится к нахождению высоты ромба. Рассмотрим равнобедренный треугольник OLK, т.к. OL=OK как радиусы одной окружности.
Далее, 
, следовательно, OH – медиана и LH=KH:
Так как OH – высота прямоугольного треугольника OAB, то