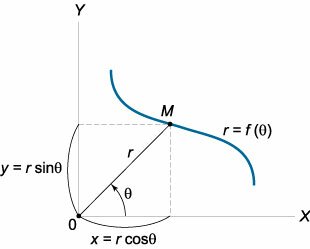
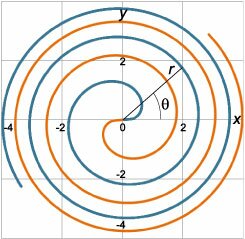
Производная окружности в полярных координатах (6 видео)

Производная окружности в полярных координатах

Равенство (r = fleft( theta right)), выражающее зависимость длины радиус-вектора (r) от полярного угла (theta), описывает на плоскости некоторую кривую и называется полярным уравнением кривой .

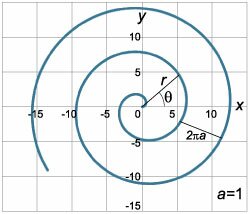
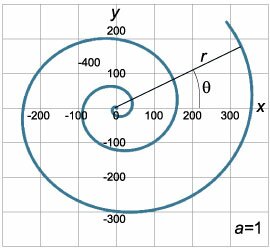
Например, Архимедова спираль (рис.(2)) описывается полярным уравнением [r = atheta ,] где (a) − параметр, определяющий плотность витков спирали. Шаг спирали (расстояние между соседними витками) является для спирали Архимеда постоянной величиной, равной (2pi a).

Переход от полярных координат (left( right)) к прямоугольным декартовым координатам (left( right)) производится по формулам [x = rcos theta ,;;y = rsin theta .] Если некоторая кривая задана полярным уравнением (r = fleft( theta right)), то в декартовых координатах она будет описываться системой уравнений [ left < beginx &= fleft( theta right)costheta \ y &= fleft( theta right)sintheta end right., ] Видно, что фактически мы получили параметрические уравнения кривой , где роль параметра (t) играет (theta). В таком случае производную полярной кривой можно найти по формуле производной параметрически заданной функции [ <frac<><> = = frac<<>><<>> > = <frac<<<<left( right)>^prime >>> <<<<left( right)>^prime >>> > = <frac<><>.> ] Рассмотрим примеры вычисления производных для некоторых полярных кривых.

Уравнение Архимедовой спирали (рис.(2)) в полярных координатах записывается в виде [r = fleft( theta right) = atheta .] Производная (largefrac<><>normalsize) находится по формуле [ <frac<><> = = frac<<>><<>> > = <frac<><>.> ] Подставляя функцию (fleft( theta right)), имеем [ <frac<><> = frac <<<<left( right)>^prime >sin theta + atheta costheta >> <<<<left( right)>^prime >costheta — atheta sin theta >> > = <frac<><> > = <frac<><>.> ] Разделим числитель и знаменатель на () (полагая, что (theta ne largefracnormalsize + pi n,;n in mathbb)). Тогда для производной получается такое выражение: [frac<><> = frac<><>.] Последнюю формулу можно еще упростить, если воспользоваться тригонометрическим соотношением [tan left( right) = frac<><>.] Для этого представим угол (theta) как [theta = tan left( right).] В результате получаем [ <frac<><> = frac<><> > = <frac<<tantheta + tan left( right)>> <<1 — tan theta cdot tan left( right)>> > = <tan left( right).> ] Интересно, что производная спирали Архимеда не зависит от длины радиуса (r), а определяется только углом (theta). В этом проявляется свойство самоподобия архимедовой спирали. Данная особенность свойственна и многим другим плоским кривым.

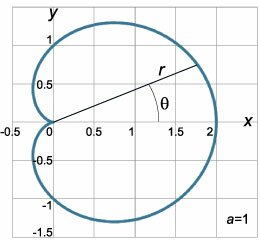
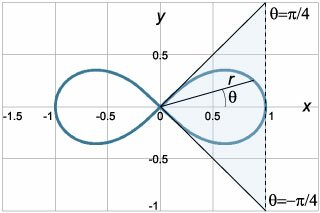
Кривая кардиоиды (рис.(3)) напоминает изображение сердца (отсюда происходит ее название) и обладает рядом замечательных свойств.

Красивые математические объекты и структуры одного и того же типа часто возникают в различных областях, которые на первый взгляд совершенно не связаны друг с другом. Такие примеры вновь заставляют нас задумываться об удивительном единстве окружающего мира и природы. Так, кардиоида совершенно неожиданно появляется в знаменитом фрактальном множестве Мандельброта , занимая его центральную часть (рис.(4)).

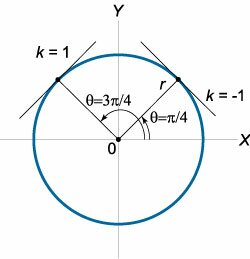
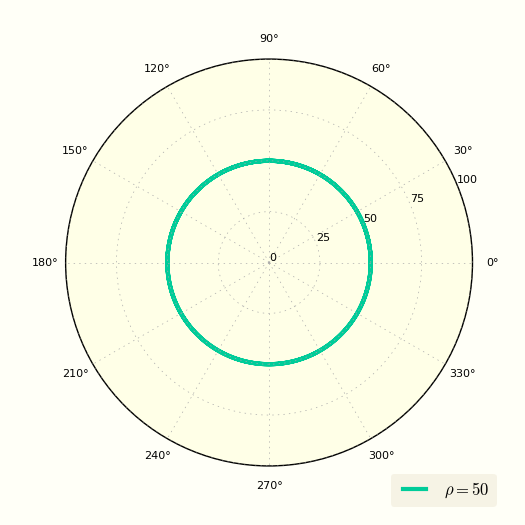
Уравнение окружности в полярных координатах имеет очень простой вид: [r = fleft( theta right) = R,] где (R) − радиус окружности.

Отсюда, учитывая, что (f’left( theta right) = 0), легко находится производная (largefrac<><>normalsize) окружности: [ <frac<><> = = frac<<>><<>> > = <frac<><> > = <frac<><> > = ] В частности, для углов (largefracnormalsize) и (largefracnormalsize) производная равна: [ <frac<><>left( <theta = frac> right) = — cotfrac = — 1,>;; <frac<><>left( <theta = frac<>> right) = — cotfrac<> = 1.> ] Как известно, значение производной в некоторой точке равно угловому коэффициенту (тангенсу угла наклона) касательной, проведенной к кривой в этой точке. Для указанных двух углов это схематически показано на рисунке (7).

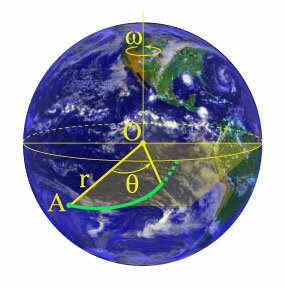
Спираль Галилея описывает траекторию свободно падающего тела в системе координат, учитывающей вращение Земли. Выведем ее уравнение в полярных координатах.

Пусть тело начинает падать из некоторой точки (A), расположенной над экватором Земли (рис.(9)). Движение вдоль радиус-вектора (r) является равноускоренным и определяется соотношением [r = H + R — frac<<g>>,] где (H) − начальная высота тела над уровнем Земли, (R) − радиус Земли, (g) − ускорение свободного падения, (t) − время.

Одновременно с падением тела происходит вращение Земли с постоянной угловой скоростью (omega). В таком случае угол поворота (theta) изменяется со временем по закону [theta = omega t = frac<>t,] где (omega) − угловая скорость вращения Земли, (T) − период вращения ((T = 24;text = 86400;text)).

Таким образом, параметрические уравнения кривой имеют вид: [left< begin r = H + R — frac<<g>>\ theta = frac<>t end right..] Исключая параметр (t), получим полярное уравнение данной траектории: [ <t = frac<>theta ,>;; <Rightarrow r = H + R — frac<left( <frac<>theta > right)^2> > = <H + R — frac<<g>><<8>>.> ] Это уравнение удобнее записать в такой форме: [ <rleft( theta right) = a- d,>;; <text;;a = — frac<<g>><<8>>,>;; <d = — left( right).> ] Данное уравнение называется полярным уравнением спирали Галилея . В рассмотренной модели один виток спирали соответствует одному обороту Земли. Ясно, что при реальных временах падения траектория тела описывается достаточно коротким участком спирали.

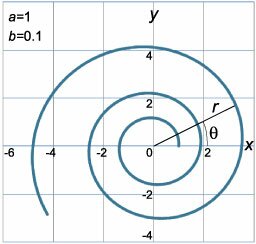
Акцентируя внимание на переменном (квадратичном) члене (a), рассмотрим далее случай (d = 0.) Тогда уравнение спирали принимает следующий вид: [r = fleft( theta right) = a.] Как видно на рисунке (10), спираль Галилея похожа на спираль Архимеда, но отличается от нее тем, что с увеличением угла длина радиус-вектора возрастает гораздо быстрее — в соответствии с квадратичным законом. По такому же закону возрастает и шаг спирали Галилея.

Возвращаясь к теме задачи, вычислим производную (largefrac<><>normalsize) заданной кривой.

Содержание

Окружность в полярных координатах
Построение окружности по простому уравнению в полярной системе координат
Еще одно уравнение окружности в полярных координатах
Уравнение окружности в полярных координатах
Построение окружности в полярной системе координат
Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах
Производная окружности в полярных координатах
🎦 Видео

Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

Окружность в полярных координатах

Уравнение окружности в полярных координатах выглядит очень просто

Это уравнение показывает, что ρ вообще не зависит от угла φ.

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Построение окружности по простому уравнению в полярной системе координат

Видео:Двойной интеграл в полярных координатахСкачать

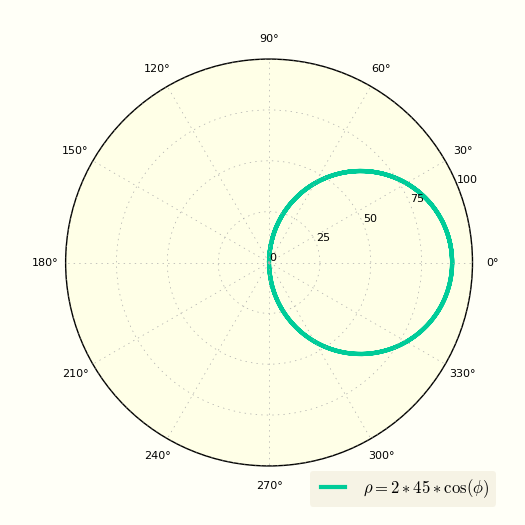
Еще одно уравнение окружности в полярных координатах

Первый пример был очень простым, теперь возьмем окружность смещенную по оси X в декартовых координатах и получим ее полярное уравнение.

Известно, что окружность в декартовой прямоугольной системе координат описывается уравнением:

Используя эти формулы и подставив их в (1) мы получим:

Видео:§2 Различные уравнения окружностиСкачать

Уравнение окружности в полярных координатах

Изначально после подстановки имеем

И этого уравнения получается система

Первое уравнение системы описывает полюс окружности.

Второе описывает саму окружность в полярной системе координат.

В итоге получаем:

Видео:Полярная система координатСкачать

Построение окружности в полярной системе координат

Видео:Оператор Лапласа в полярных координатахСкачать

Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах

В данном варианте мы сместим окружность по оси Y в декартовых координатах и получим ее полярное уравнение.

При таком смещении окружность описывается уравнением:

И этого уравнения получается система

Первое уравнение системы описывает полюс окружности.

Второе описывает саму окружность в полярной системе координат.

Видео:Скорость и ускорение точки в полярных координатахСкачать

Производная окружности в полярных координатах

Построим график функции в полярных координатах r=r(φ),
где 0 Выражения могут состоять из функций (обозначения даны в алфавитном порядке): absolute(x) Абсолютное значение x
(модуль x или |x|) arccos(x) Функция — арккосинус от x arccosh(x) Арккосинус гиперболический от x arcsin(x) Арксинус от x arcsinh(x) Арксинус гиперболический от x arctg(x) Функция — арктангенс от x arctgh(x) Арктангенс гиперболический от x exp(x) Функция — экспонента от x (что и e^x) log(x) or ln(x) Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) sin(x) Функция — Синус от x cos(x) Функция — Косинус от x sinh(x) Функция — Синус гиперболический от x cosh(x) Функция — Косинус гиперболический от x sqrt(x) Функция — квадратный корень из x sqr(x) или x^2 Функция — Квадрат x ctg(x) Функция — Котангенс от x arcctg(x) Функция — Арккотангенс от x arcctgh(x) Функция — Гиперболический арккотангенс от x tg(x) Функция — Тангенс от x tgh(x) Функция — Тангенс гиперболический от x cbrt(x) Функция — кубический корень из x gamma(x) Гамма-функция LambertW(x) Функция Ламберта x! или factorial(x) Факториал от x