Окружность движется по синусоиде (3 видео)

Естественная анимация в интерфейсах

Анимация в интерфейсе делает наглядным изменение его состояния. Например, при неудачной отправке длинная форма прокручивается к неправильно заполненному полю. Или увеличивающаяся по нажатию фотография раздвигает окружающие элементы.

Без анимации сложнее воспринимать резкие и внезапные изменения. Вместе с тем анимация должна быть короткой и ненавязчивой, чтобы не мешать пользователю.

Анимация кажется естественной, когда повторяет привычное движение предметов окружающего мира. Под катом я расскажу, как делал анимацию на основе физических законов. Смотрите готовый результат на демо-странице (там один блок следует за другим при движении мыши).

Содержание

Вспоминаем физику
Как провести синусоиду через две точки
Приближенное решение
Применение
Синусоида — свойства, формула и график функции
Основные понятия
Особенности построения
Свойства и доказательства
Нечётность и постоянство
Больше и меньше
Окружность движется по синусоиде
📺 Видео

Видео:Тригонометрическая окружность для непонимающихСкачать

Вспоминаем физику

Перемещение объектов описывается изменением координат x с течением времени t. Если вы попытаетесь подобрать функцию x(t) «на глазок», вы потратите много времени, добиваясь плавного и естественного движения. Что выбрать? Гиперболу? Параболу? Куда ее переместить? Как повернуть?

За примерами движения лучше всего обратиться к предметам окружающего мира. Математический закон их движения диктуется физикой. Толкнем брусок, лежащий на столе. Он проходит определенное расстояние, замедляясь под действием силы трения. В хорошем приближении сила сухого трения скольжения постоянна, и зависимость x(t) оказывается параболой. Такое замедление можно использовать, если в начальный момент объект анимации уже двигался.

Рис. 1. Торможение сухим трением по параболе

Сила вязкого трения пропорциональна скорости движения тела. В таком случае тело будет двигаться к точке остановки по экспоненте за бесконечно большое время. Если экспоненту исказить, чтобы ограничить время движения, такая анимация будет казаться неестественной. Из-за трудностей с остановкой в разумное время не следует использовать модель вязкого трения, только если симуляция самого вязкого трения не является целью.

Рис. 2. Торможение по экспоненте в вязкой среде

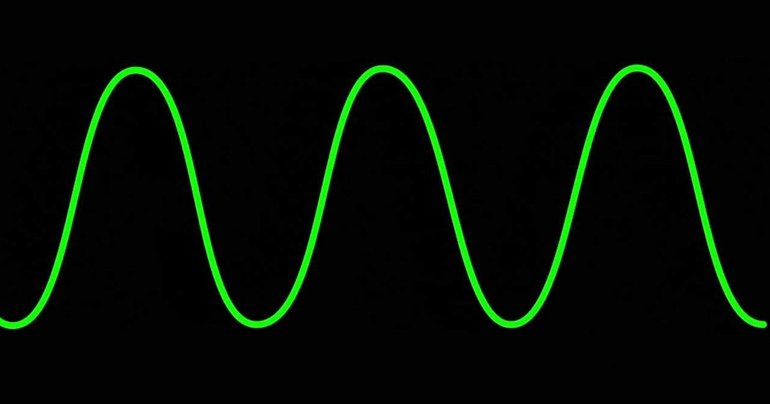
Отклоненный от положения равновесия маятник (или грузик на пружине) плавно набирает скорость, проходит положение равновесия и плавно тормозит. Затем движение повторяется в обратную сторону, и так до бесконечности (если трения нет). График такого движения — синусоида. Периодический повтор нам не особо интересен, а вот движение маятника между крайними точками получается плавным и естественным.

Рис. 3. Движение маятника по синусоиде между крайними точками

В JS-библиотеках и CSS есть заготовки easing-функций для создания специальных эффектов. Почти все заготовки следует использовать в специальных случаях, с осторожностью. Только синусоида более-менее универсальна.

Во-первых, синусоидальная траектория переводит тело из одного покоящегося положения в другое. Во-вторых, продолжительность такого движения равна половине периода. Движение ограничено во времени. Продолжительность не зависит от внешних обстоятельств и начальных условий. Она зависит только от свойств самой системы и определяется соотношением жесткости и инерционности.

Обычно я выбираю длительность анимации по синусоиде в 200 миллисекунд. Такая длительность в несколько раз больше времени реакции человека. Анимация хорошо заметна, но не успевает раздражать.

Давайте научимся проводить синусоидальную траекторию по начальным условиям, времени движения и точке остановки.

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Как провести синусоиду через две точки

Пусть тело покоится в начальный и конечный момент времени. Тогда касательные к графику в точках t₁ и t₂ горизонтальны, а сам график — это полупериод синусоиды.

Рис. 4. График движения между двумя положениями покоя

Уравнение, описывающее полупериод синусоиды, легко подобрать:

После окончания одной анимации мы можем начинать другую опять по этой формуле. Но что делать, если новая анимация должна начаться, пока еще не закончилась старая? Чтобы обеспечить плавность движения, мы останавливаем текущую анимацию (синяя линия) и начинаем новую анимацию (красная линия) с ненулевой начальной скоростью:

Рис. 5. График движения с ненулевой начальной скоростью

Без математических вычислений не получится написать формулу, соответствующую красной линии. Давайте проделаем эти вычисления.

Семейство всех возможных синусоид описывается уравнением

с четырьмя неизвестными параметрами A, B, C и 0″/>. Я сдвинул начало отчета времени в точку t₂, чтобы сразу избавиться от второго слагаемого. Действительно, производная должна быть нулевой, потому что касательная в точке t₂ горизонтальна. Это возможно, когда B=0.

Так как , то подставляя в (1), получаем . Отсюда исключаем C:

Продифференцируем, чтобы найти скорость

Нам известно положение x₁ и скорость v в начальный момент времени:

Из этой системы уравнений нужно найти A и . Пора вводить новую переменную вместо . Ее смысл — разность фаз синусоиды в начальной и конечной точке. Например, для графика на рис. 4 , потому что на промежутке укладывается полупериод синусоиды. На рис. 5 , потому что меньше половины периода.

После подстановки и небольших преобразований приходим к системе

Разделим почленно первое уравнение на второе:

Параметр в правой части известен заранее. Он определяет требуемый характер движения. Если , то начальная скорость мала, тело сначала должно ускориться. Если , начальная скорость велика, тело должно замедляться.

Тригонометрические функции в левой части сводятся к тангенсу половинного угла. В итоге у нас нелинейное уравнение относительно k:

Проанализировать его решения можно на графике. Нарисуем график левой и правой части при некоторых значениях параметра :

Рис. 6. Графическое решение уравнения (2)

Обсудим получившиеся решения.

Рассмотрим точку A. Это решение существует при 1/2″/> и соответствует изображенному на рисунке 5: . Как ожидалось, . В пределе нулевой скорости , красная прямая совпадет с осью ординат, точка A уйдет по тангенсоиде в бесконечность. В этом пределе . Пока всё идет правильно.

Точка C отвечает значению . Такое случается, когда тело в первый момент времени движется вперед, а надо двигаться назад. Теперь . Движение описывается фрагментом синусоиды, большим чем полупериод, но меньшим, чем период:
. Тело тормозит, останавливается, движется назад и останавливается в требуемом месте.

Из графика видно, что при точка B попадает в диапазон . Тело пройдет по синусоиде больше, чем полный период колебаний: . Причина такого странного решения в том, что точка остановки находится слишком близко по сравнению с характерным расстоянием . Поэтому провести синусоиду без дополнительной остановки и возврата не получится.

Видео:Построение синусоидыСкачать

Приближенное решение

Мы решили математическую задачу проведения синусоиды, но жизнь от этого проще не стала. Во-первых, чтобы определить параметры синусоиды, надо решить нелинейное уравнение (2). Привет, итерационные методы! Во-вторых, уравнение имеет бесконечное количество решений, а требуемое решение не всегда существует.

Эти трудности возникли от того, что мы зафиксировали продолжительность анимации ровно в 200 миллисекунд. Однако ничего страшного не случится, если анимация продлится, скажем, 180 миллисекунд. Или даже 250 миллисекунд. Нам важнее остановка в заданном месте, а точной продолжительностью анимации мы пожертвуем для упрощения расчетов.

Ослабив требования на продолжительность анимации, мы проделаем такой трюк. Предположим, что у нас есть приближенное решение нелинейного уравнения (2). Оно является точным решением уравнения с другим параметром

Ему соответствует другое время окончания анимации:

Теперь неизвестные параметры траектории A и элементарно выражаются через и .

Я подобрал подходящее для наших целей приближение к уравнению (2):

Синяя сплошная линия соответствует точному уравнению (2), а красная пунктирная — его приближению:

Рис. 7. Сравнение точного соотношения (2) и его приближения

А еще в случае предлагаю взять чуть больше, чем 1/2, и сократить время анимации, чтобы избежать отскока и возврата.

Видео:Тригонометрическая окружность. Как выучить?Скачать

Применение

Код и сферический пример использования есть на демо-странице. Поводите мышью и посмотрите, как черный блок следует за оранжевым.

Описанная схема применяется и в готовом продукте. Я разработал ее для синхронной прокрутки исходника и предпросмотра в markdown- и latex- редакторе математических текстов.

Идею и первоначальную реализацию нашел на демо-странице js-парсера markdown-it. В их варианте анимация получилась рваной и подтормаживающей. Тому есть несколько причин:

Для анимации применяется линейная функция: $(. ).stop(true).animate(, 100, ‘linear’) . Вместо гладкого графика получается ломаная.
Анимация через jQuery().stop().animate() тормозит по сравнению с requestAnimationFrame() .
Чтобы избежать падения производительности, «проглатываются» события onscroll , следующие чаще чем 50 миллисекунд. В моем варианте такой проблемы нет. Последовательные события onscroll корректируют положение точки остановки и не замедляют анимацию.

Чтобы добиться важной для продукта качественной анимации, я проработал метод вычисления на основе физических уравнений, и реализовал его через специальный браузерный метод requestAnimationFrame() . Метод хорошо работает при любой прокрутке: клавишами PageUp/PageDown, через перемещение полос прокрутки, колесико мыши, тачпад, тачскрин.

Видео:График синуса или откуда берется синусоида?Скачать

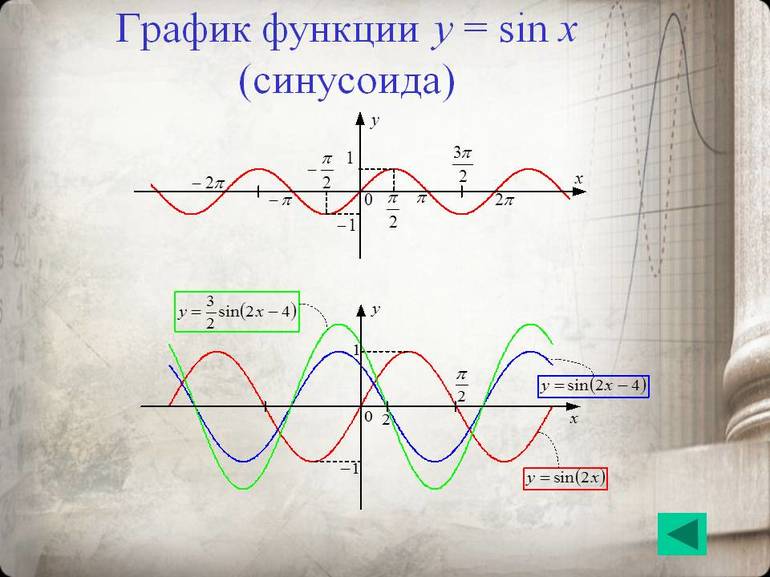
Синусоида — свойства, формула и график функции

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Основные понятия

Кривая получается из синусоидальной дуги путём смещения к пи/2 в сторону со знаком минус. Кривая представляет график функции у=sin x. В формуле синусоиды y=a+b cos (cx+d) присутствуют следующие аргументы:

a: показывает сдвиг графика синусоиды по оси Oy (чем больше значение, тем выше прямая);
b: описывает растяжения функции по оси Oy (чем выше постоянная, тем сильнее колебания);
c: определяет растяжение по оси Ох (если постоянная увеличивается, наступает период колебаний);
d: описывает сдвиг по оси Ох (если d увеличивается, тогда при построении синусоиды учитывается сдвиг в область со знаком минус по оси абсцисс).

Сжатие, растяжение либо сдвиг кривой приводит к изменению величины. Явления называются гармоническими колебаниями. Примеры синусоиды: экспонент или показательная функция в виде винтовой линии, проведённой на плоскости, скрученный провод, развёрнутый рулон бумаги.

Видео:Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

Особенности построения

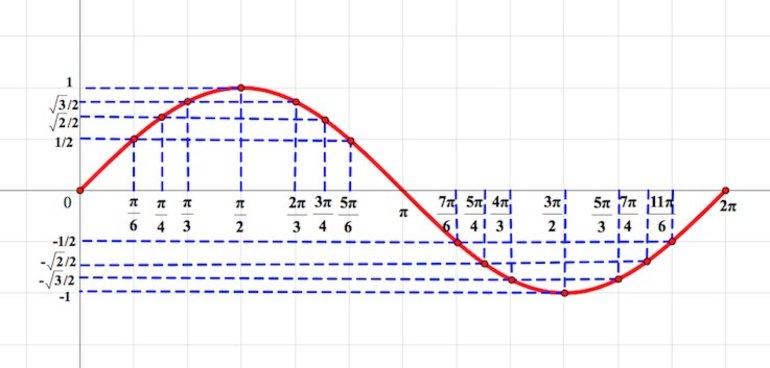
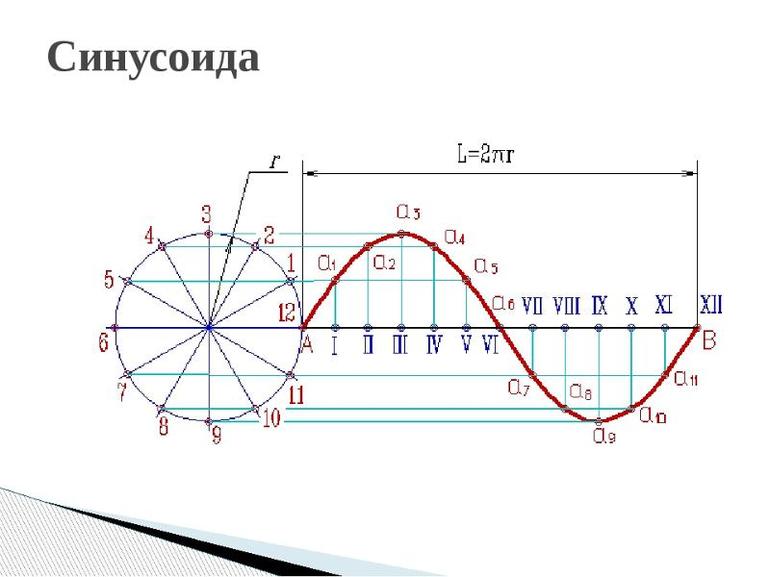
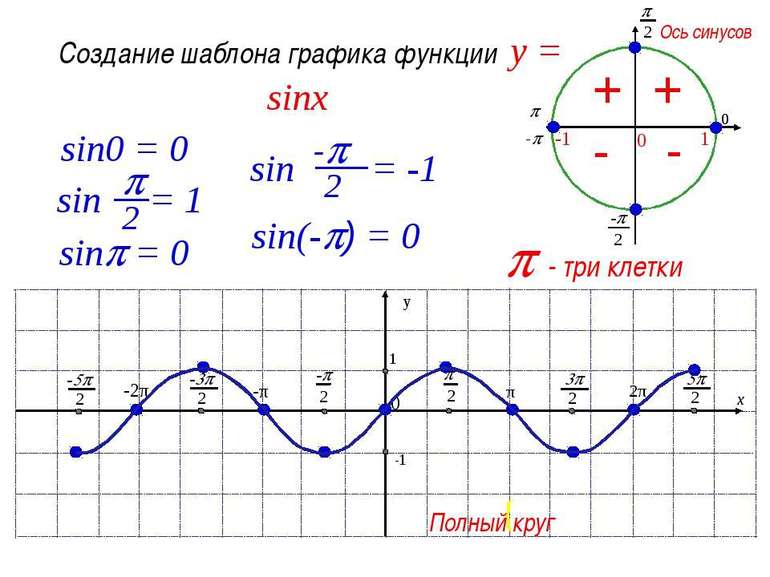
Чтобы выявить свойства синусоиды, необходимо построить её график, провести исследование синуса. В алгебре под функцией представлена плоская кривая, которая выражает закон колебания sin с учётом изменения центрального угла. Сама синусоида строится в схематической последовательности:

проводится горизонтальная ось, на которой откладывается заданная длина волны;
отрезок делится на равные части;
слева чертится окружность с радиусом, равным величине амплитуды;
окружность делится на 12 одинаковых частей;
через полученные точки проводятся прямые;
из точек проводятся перпендикуляры к оси.

График можно построить на онлайн ресурсе либо с помощью специальных программ (Excel). Для расчёта используется калькулятор, основная формула y=sin х. При решении задач учитывается длина волны, которая равна 2 пи. Такое преобразование объясняется тем, что значение функции при любом икс совпадает с её периодичностью x+2π.

Пересечение оси Ох происходит в точках перегиба πK. Максимум достигается при положительном π/2+2πK, а обратное — -π/2+2πK. Свойства кривой проявляются в частном либо комплексном виде:

размах;
растяжение/сжатие;
фазовые колебания;
круговая частота.

При сдвиге графика влево к значению пи/2 образуется косинусоида. Любое изменение величины характерно для квадрата с гармоническими колебаниями. Примеры подобных явлений: движение маятника, сбои с напряжением в электросети. Другой случай с синусоидальными колебаниями — звук. Он редко бывает чистым, соответствуя y=A sin wt, где:

А (а) — модуль неизвестной (расстояние от начала координат до точки А);
w — угловая частота;
t — время.

Чаще издаются обертоны, для которых характерны низкие амплитуды. Подобные явления изучаются в школе на уроках физики в старших классах.

Видео:Построение графиков тригонометрических функций с помощью преобразований. Практ. часть. 10 класс.Скачать

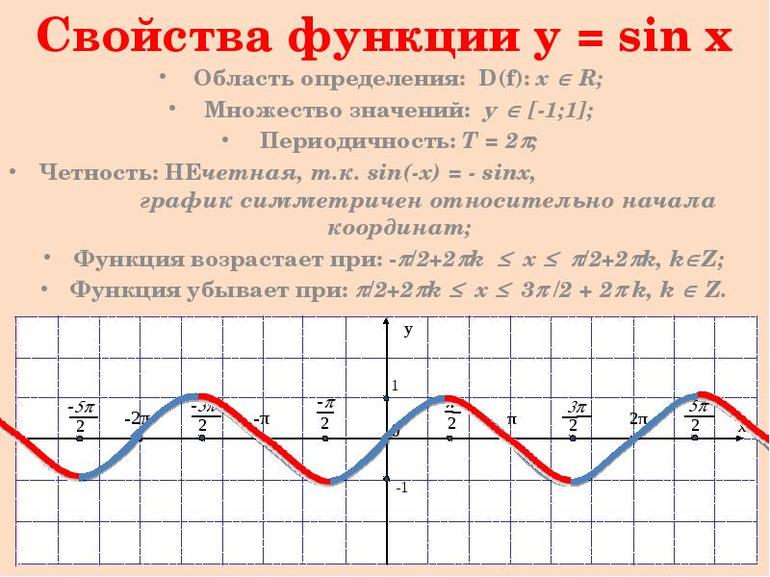
Свойства и доказательства

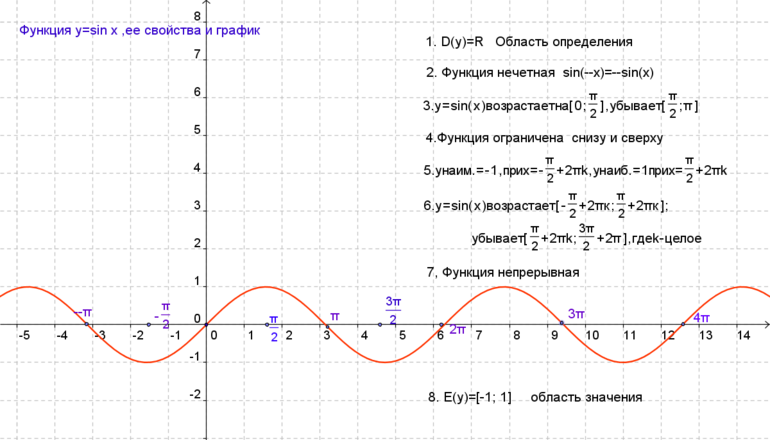
К главным свойствам синусоиды относятся область значений (включая нуль) и определений, чётность/нечётность, периодичность, точки пересечения с осью координат, промежуточности постоянства, убывания и возрастания, минимум и максимум. При пересечении графика функции (ГФ) с осью Ох результат равняется нулю. Под значением синуса подразумевается ордината соответствующей точки единичной окружности.

Так как через круг в одной области можно провести только одну прямую, перпендикулярную оси, поэтому для области определения функции подходят все числа. Такое свойство записывается следующим образом: D (sin x) = R.

Значения ординаты единичной окружности (ЕД) расположены на отрезке [—1; 1]. Они принимают значения от -1 до 1. Через любую точку указанного промежутка оси ординат, равного диаметром ЕД, проводится прямая, перпендикулярная оси ординат. Таким способом получается точка с рассматриваемой ординатой.

Из свойства вытекает следующее: функция y= sin x имеет область значений (-1; 1). Утверждение записывается так: E (sin x)=(-1; 1). Максимальное значение функции равняется единице. Подобное возможно, если соответствующей точкой ЕД является точка А. Минимальное число y равно -1 в случае, когда точкой ЕД является В (х=пи/2 +2пиk, где k принадлежит области Z.

Нечётность и постоянство

Функция считается нечётной, если sin (-x)=- sin x. Её график симметричен по отношению к началу координат. Сам синус является периодической величиной, у которой наименьший положительный период. Через отрезок 2пи вид кривой повторяется. Это свойство учитывается при построении графика.

Предварительно чертится кривая на любом отрезке соответствующей длины. При переносе линии влево и вправо соблюдается шаг в kT=2 πk, где k — любая натуральная цифра. Для вычисления точек пересечения линии с осями координат используется равенство х=0. Если значение подставить в функцию, получится следующее: y=sin 0=0. В таком случае график проходит через начало координат.

Так как y равен нулю, поэтому можно рассчитать х, воспользовавшись формулой y= sin x. Координата подходящей точки ЕД равняется нулю. Такое явление будет наблюдаться только в случае, если на ЕД будут выбраны точки D либо C, при x=πk, k принадлежит Z.

Функция имеет положительное значение в первой и во второй четвертях. На этих промежутках sin x больше нуля, а любое значение х находится в пределах 0-π. При решении задач учитывается период при всех x, принадлежащих отрезку (2πk; π+2πk), где k принадлежит Z. Функция считается отрицательной в третьем и четвёртом квадрате. При этом sin меньше нуля, а иск находится в пределах (пи+2пиk; 2пи+2пиk), k принадлежит области Z.

Больше и меньше

С учётом периодичности y с периодом T=2π исследуется функция на возрастание и убывание на любом отрезке длиной в 2пи. Если T= (-π/2;3π/2), а х принадлежит данному промежутку, тогда при увеличении аргумента изменится в большую сторону и ордината. Следовательно, на указанном отрезке синусоида возрастает.

Если учитывать её периодичность, можно прийти к выводу, что она возрастает на каждом интервале (-π/2+2πk; π/2+2πk), k принадлежит Z. Если х находится на отрезке (-π/2;3π/2), тогда при увеличении аргумента ордината ЕД уменьшается, а функция убывает. С учётом периодичности синусоиды можно сделать вывод, что она бывает на каждом отрезке (π/2+2πk;3π/2+2πk), k находится в области Z.

Основываясь на проведённом исследовании, строится график y=sin x. С учётом периодичности 2π предварительно строится график на любом отрезке соответствующей длины. Чтобы точно построить точки, рекомендуется придерживаться значения синуса (ордината ЕД). На основе нечётности проводится кривая, симметричная началу координат. При этом необходимо придерживаться интервала (-π;0). Так как линия строится на отрезке длиной 2π, поэтому учитывается периодичность величины.

Вид графика повторяется на каждом отрезке с аналогичной длиной. Таким способом получается синусоида. Рассматриваемая тригонометрическая функция получила широкое применение в технике, физике и математике. Большинство процессов, включая колебания струн, напряжения в цепи, описываются с помощью функции, задаваемой формулой y= A sin (wx + f). Подобные явления считаются гармоническими колебаниями.

Кривая получается из синусоиды за счёт разных колебаний и путём параллельного переноса вдоль оси Ох. Чаще изменения результата связаны с функцией времени t. В таком случае используется формула y= A sin (wx + f), где через А обозначается амплитуда колебания, через w — частота, f — начальная фаза, 2пи/f — период колебания.

Видео:Центростремительное ускорение. 9 класс.Скачать

Окружность движется по синусоиде

При обсуждениях мне пришлось столкнуть вот с таким. Оппонент решил ткнуть носом и обосновать период по другой методике, нежеле той, которая имелась у Гюйгенса.

Конечно, спорить с каждым случаем достаточно сложное занятие чисто по временным затратам. Если еще и торопишься, то неизбежны ошибки, я их не боюсь и готов признать, если таковые найдутся.

Приходится иногда напоминать, что я рассматриваю только первоначальные доказательства, а не вторичные, хоть даже и через двести, триста лет. В принципе Достаточно одной зацепки, чтоб найти слабое место и развалить все здание на корню, поскольку это фундамент всего остального, позднейших наслоений, при помощи чего пытаются обосновать справедливость самого основного, и явно ошибочного,

Что и сделано в данной статье.

Однако умельцы от академической физ — мат-тех направленности, подсовывают иногда интересный материал, который никак пропустить невозможно.

В пылу обсуждения мне заявили, что период колебаний тот же самый (с 2пи) у пружинного маятника, и у колебательного контура.

Функция f ( t ) является периодической с периодом Т,
если при всех значениях её аргумента t
выполняется соотношение
f ( t+T )= f ( t )

В частности, функция f ( t )= sin ( pt ) будет периодической с периодом T=2Пи / p

Проводим проверку периодичности, т.е. проверку выполнения условия sin ( pt )= sin ( p *( t+T ) )
sin ( pt )= sin ( p * ( t+T ) )= sin ( pt+pT ) = sin ( pt + 2Пи p / p ) = sin ( pt+ 2Пи) что и тр-сь доказать

Т аким образом, синусоида будет возвращаться к своему состоянию (совершать полное колебание) через время
T= 2Пи / p
Движение описывается одним и тем же уравнением
для угла отклонения Fi математического маятника
d2Fi / dt2= — l / g Fi

или для смещения X груза пружинного маятника
d2X / dt2 = — k / m X
или для напряжения U на конденсаторе C колебательного контура LC
d2U/dt2 = — (1/LC) U

Потому решение всех трех задач о колебаниях будет подобным
Fi , X, U = sin ( pt )
где
p= sqrt ( g / l ) для математического
p=sqrt ( k / m ) для пружинного
p=sqrt ( 1/LC ) для колебательного контура

Соответственно периодом будет
для математического 2Пи * sqrt ( l / g )
для пружинного 2Пи * sqrt ( m / k )
для колебательного контура 2Пи * sqrt (LC )

возражения не принимаются.

Только один вопрос, а с чего вы взяли, что колебание маятника синусода ?

Замечательно математики обходятся без физики. У них движение по окружности ничем не отличается от колебания, Они даже саму статью прочесть не в состоянии, где про это принципиальное различие и говориться в самом начале.

Движение по окружности равномерное и якобы движение по синусоиде не являются возвратно-поступательными. Там нет торможений с остановками, нет угловых ускорений изменяющих свое направление.

И подкладывание движущегося равномерно листка бумаги под кончик маятника, рисующего якобы синусоиду, является уже совместным движением двух тел, это, во-первых. И, во-вторых, маятник собственно не движется по кривой, он просто рисует, эта линия произведение маятника с использованием приспособления, а не он ее творение.

А вот давайте и разберем, что может изображать эта кривая для начала.

Красным обозначена точка равновесия, которую маятник проходит дважды.

Сам угол отклонения может быть любым, и путь, который маятник проходит по дуге окружности, заданной этим углом, тоже может быть любым. И именно аналог этого полного пути рисует маятник и никакого другого, это часть окружности в ту и другую сторону. И они, половики, естественно равны. Но Н икаких тут периодов 2пи от синуса не наблюдается, нет туда обратно 360 градусов, кроме одного единственного случая приведенного в статье.

То есть с полным правом можем дать такое пояснение: