Около любого ромба можно описать окружность в любой треугольник

Какие из следующих утверждений верны?

1) Около любого ромба можно описать окружность.

2) В любой треугольник можно вписать не менее одной окружности.

3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.

4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.

Проверим каждое из утверждений.

1) «Около любого ромба можно описать окружность.»— неверно, чтобы около четырёхугольника можно было описать окружность, необходимо, чтобы сумма противоположных углов четырёхугольника составляла 180°. Это верно не для любого ромба.

2) «В любой треугольник можно вписать не менее одной окружности.» — верно, в любой треугольник можно вписать окружность.

3) «Центром окружности, описанной около треугольника, является точка пересечения биссектрис.» — неверно, центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров треугольника.

4) «Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.» — неверно, центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника.

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

• Треугольник
• Выпуклый, правильный многоугольник
• Квадрат
• Равнобедренная трапеция
• Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

1. В любой треугольник может быть вписана окружность, причем только один раз.
2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
3. Вписанная окружность касается всех сторон треугольника.
4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac(a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Примеры вписанной окружности

• Треугольник
  
• Четырехугольник
  
• Многоугольник
  

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

1. Радиус вписанной окружности в треугольник и радиус вписанной
   в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
4. В любой ромб можно вписать окружность. Верное утверждение.
5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
7. Угол вписанный в окружность равен соответствующему центральному
   углу опирающемуся на ту же дугу. Неверное утверждение.
8. Радиус вписанной окружности в прямоугольный треугольник равен
   половине разности суммы катетов и гипотенузы. Верное утверждение.
9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
10. Вписанная окружность в треугольник имеет в общем
    три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

Около ромба можно описать окружность в любой треугольник

Около ромба можно описать окружность в любой треугольник

Какие из следующих утверждений верны?

1) Около любого ромба можно описать окружность.

2) В любой треугольник можно вписать не менее одной окружности.

3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.

4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.

Проверим каждое из утверждений.

1) «Около любого ромба можно описать окружность.»— неверно, чтобы около четырёхугольника можно было описать окружность, необходимо, чтобы сумма противоположных углов четырёхугольника составляла 180°. Это верно не для любого ромба.

2) «В любой треугольник можно вписать не менее одной окружности.» — верно, в любой треугольник можно вписать окружность.

3) «Центром окружности, описанной около треугольника, является точка пересечения биссектрис.» — неверно, центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров треугольника.

4) «Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.» — неверно, центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника.

В любом ромбе можно описать окружность

В любом ромбе можно описать окружность

Какие из следующих утверждений верны?

1) Около любого ромба можно описать окружность.

2) В любой треугольник можно вписать не менее одной окружности.

3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.

4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.

Проверим каждое из утверждений.

1) «Около любого ромба можно описать окружность.»— неверно, чтобы около четырёхугольника можно было описать окружность, необходимо, чтобы сумма противоположных углов четырёхугольника составляла 180°. Это верно не для любого ромба.

2) «В любой треугольник можно вписать не менее одной окружности.» — верно, в любой треугольник можно вписать окружность.

3) «Центром окружности, описанной около треугольника, является точка пересечения биссектрис.» — неверно, центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров треугольника.

4) «Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.» — неверно, центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника.

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

• Треугольник
• Выпуклый, правильный многоугольник
• Квадрат
• Равнобедренная трапеция
• Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

1. В любой треугольник может быть вписана окружность, причем только один раз.
2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
3. Вписанная окружность касается всех сторон треугольника.
4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac (a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Примеры вписанной окружности

• Треугольник
  
• Четырехугольник
  
• Многоугольник
  

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

1. Радиус вписанной окружности в треугольник и радиус вписанной
   в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
4. В любой ромб можно вписать окружность. Верное утверждение.
5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
7. Угол вписанный в окружность равен соответствующему центральному
   углу опирающемуся на ту же дугу. Неверное утверждение.
8. Радиус вписанной окружности в прямоугольный треугольник равен
   половине разности суммы катетов и гипотенузы. Верное утверждение.
9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
10. Вписанная окружность в треугольник имеет в общем
    три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

Ромб. Формулы, признаки и свойства ромба

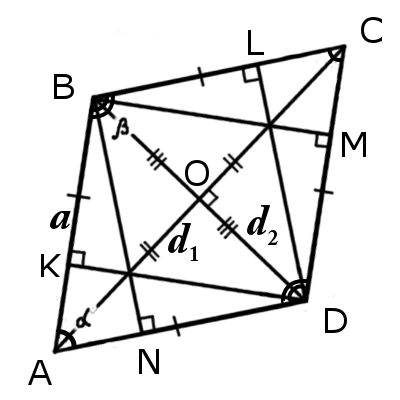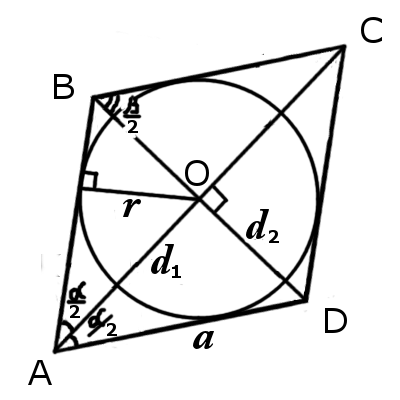Рис.1	Рис.2

Признаки ромба

∠BAC = ∠CAD или ∠BDA = ∠BDC

Δ ABO = Δ BCO = Δ CDO = Δ ADO

Основные свойства ромба

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

AC 2 + BD 2 = 4AB 2

Сторона ромба

Формулы определения длины стороны ромба:

1. Формула стороны ромба через площадь и высоту:

2. Формула стороны ромба через площадь и синус угла:

3. Формула стороны ромба через площадь и радиус вписанной окружности:

4. Формула стороны ромба через две диагонали:

5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):

6. Формула стороны ромба через большую диагональ и половинный угол:

7. Формула стороны ромба через малую диагональ и половинный угол:

8. Формула стороны ромба через периметр:

Диагонали ромба

Формулы определения длины диагонали ромба:

d ₁ = a √ 2 + 2 · cosα

d ₁ = a √ 2 — 2 · cosβ

d ₂ = a √ 2 + 2 · cosβ

d ₂ = a √ 2 — 2 · cosα

d ₁ = 2 a · cos ( α /2)

d ₁ = 2 a · sin ( β /2)

d ₂ = 2 a · sin ( α /2)

d ₂ = 2 a · cos ( β /2)

7. Формулы диагоналей через площадь и другую диагональ:

8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:

Периметр ромба

Периметром ромба называется сумма длин всех сторон ромба.

Длину стороны ромба можно найти за формулами указанными выше.

Формула определения длины периметра ромба:

Площадь ромба

Формулы определения площади ромба:

4. Формула площади ромба через две диагонали:

5. Формула площади ромба через синус угла и радиус вписанной окружности:

6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):

Окружность вписанная в ромб

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба:

2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:

3. Формула радиуса круга вписанного в ромб через площадь и синус угла:

4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:

5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:

6. Формула радиуса круга вписанного в ромб через две диагонали:

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Описанная окружность

Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема

Доказательство

Дано: произвольный АВС.

Доказать: около АВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.

Замечание 1

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Доказательство

Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Доказательство

Дано: четырехугольник АВСD, BАD + BСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)

Углы ВFD и FDE — вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.

BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .

Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 — ( В + F). (2)

В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)

F и ВFD — смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 — ВFD = 180 0 — ВАD. (4)

Подставим (3) и (4) в (2), получим:

С = 180 0 — (ЕF + 180 0 — ВАD) = 180 0 — ЕF — 180 0 + ВАD = (ВАD — ЕF), следовательно, СВАD.

А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.

Примечание:

Окружность всегда можно описать:

Поделись с друзьями в социальных сетях: