Координаты центра тяжести четверти окружности

Видео:Видеоурок 3. Определение центра тяжести.Скачать

Статические моменты площади сечения. Центр тяжести площади сечения

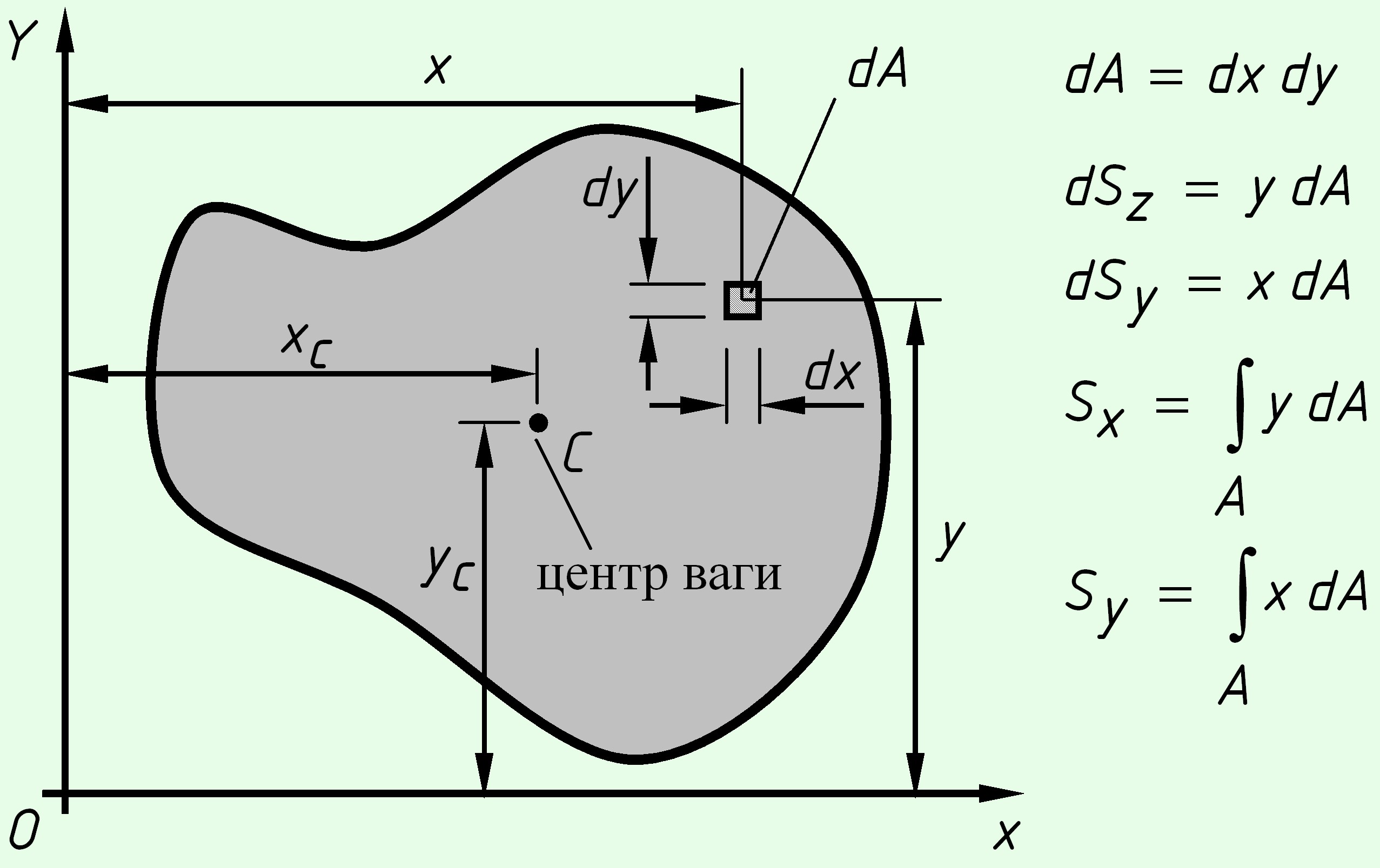
Рассмотрим произвольное поперечное сечение стержня, связанный с координатными осями $XOY$ и выделим элемент площади $dA$ с координатами ($x,y$).

Статическим моментом площади сечения относительно оси называется сумма (интеграл) по всей площади сечения от произведения площади элементарной площадки на расстояние до рассматриваемой оси.

Для сечений, для которых известны площади $A$ и координаты центров тяжести $$, $$, статические моменты площадей рассчитываются по формулам:

Статический момент площади сечения может быть положительным, отрицательным и равняться нулю.

Оси, относительно которых статические моменты площади сечения равны нулю, называются центральными.

Видео:Определение центра тяжести сложных сечений. Фигуры из ГОСТ.Скачать

Примеры определения статических моментов

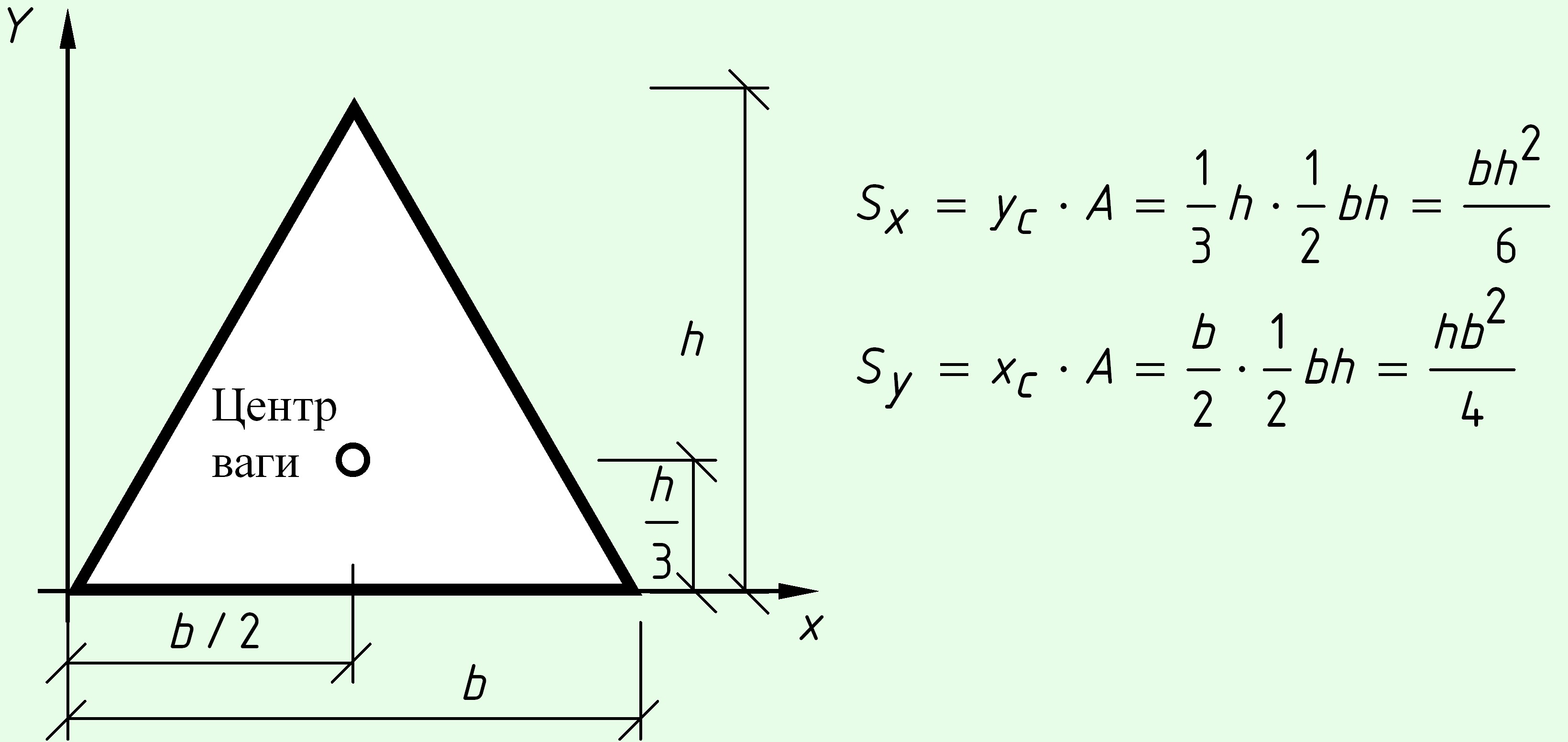
Треугольник.

Поскольку положение центра тяжести треугольника нам известно, его статический момент площади можно определить как произведение площади на соответствующую координату центра тяжести.

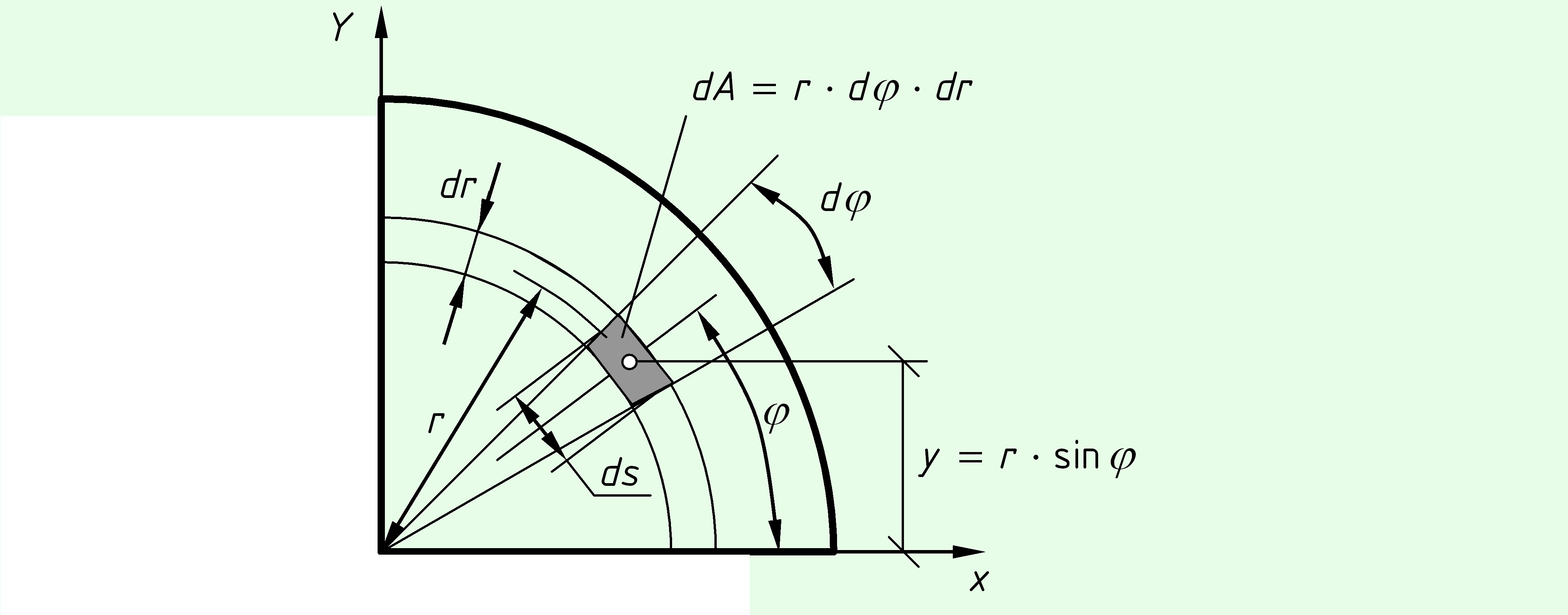
Четверть круга.

Поскольку положение центра тяжести четверти круга мы не знаем, определим статические моменты по общей формуле. Выделим элементарную площадь $dA$ с углом $dvarphi $ и высотой $dr$. Ширина площадки $ds = r cdot dvarphi ,$.

Площадь $A = frac cdot pi $.

Аналогично относительно другой оси $ = frac<<>> = frac<><>$.

Статический момент составного сечения равен сумме статических моментов его составляющих.

Тогда положение центра тяжести составного сечения запишется так:

Видео:Координаты центра тяжести пластиныСкачать

Статические моменты и координаты центра тяжести

Видео:Определение центра тяжести сложной фигуры. СопроматСкачать

Вычисление статических моментов и координат центра тяжести кривой

а) Пусть материальная точка массы отстоит от оси на расстоянии . Статическим моментом этой точки относительно оси называют число . Статическим моментом системы материальных точек , расположенных по одну сторону от оси , массы которых равны , а расстояния от оси равны называют число

Если же эти точки расположены по разные стороны от оси, то для точек, находящихся по одну сторону оси, расстояния берутся положительными, а для точек по другую сторону от оси — отрицательными.

Поэтому если точки расположены на координатной плоскости,

где — статический момент относительно оси и — относительно оси .

б) Рассмотрим теперь случай, когда масса равномерно распределена по некоторой кривой или по некоторой области . Будем считать, что плотность распределения равна единице. Тогда масса дуги численно равна ее длине, а масса области — ее площади.

Начнем со случая кривой линии , задаваемой уравнением , причем предположим, что функция непрерывна и неотрицательна.

Как обычно, разобьем отрезок на части точками и обозначим через и наименьшее и наибольшее значения функции на отрезке , Этому разбиению соответствует разбиение дуги на части (рис. 60). Из физических соображений ясно, что статический момент части относительно оси абсцисс заключен между и , где —длина этой части, (напомним, что мы положили линейную плотность дуги равной единице). Таким образом,

Так как на отрезке выполняется неравенство

то в тех же границах, что и , заключен интеграл . Значит,

Этот интеграл обозначают также следующим образом: или .

Физики обычно заменяют проведенное рассуждение более коротким. Они берут «бесконечно малый участок дуги» . Его статический момент равен . А статический момент всей дуги равен сумме элементарных статических моментов, т. е. . Преимуществом этого вывода является его наглядность. Однако в нем не определено, что такое «бесконечно малый участок дуги», или как еще говорят, «элемент дуги». При уточнении этого понятия мы вновь приходим к более длинному выводу, изложенному ранее. В дальнейшем для краткости изложения мы будем использовать принятый в физике метод рассуждений. С его помощью сразу выводим, что

Как формула (1), так и формула (2) верны и в случае, когда кривая пересекает оси координат.

в) Введем понятие центра тяжести.

Определение. Центром тяжести тела называется такая точка , что если в ней сосредоточить всю его массу, то статический момент этой точки относительно любой оси будет равен статическому моменту всего тела относительно той же оси.

Обозначим через и расстояния центра тяжести кривой от осей ординат и абсцисс.

Тогда, пользуясь определением центра тяжести кривой, получим:

Разрешая полученные равенства относительно и , найдем координаты центра тяжести плоской кривой

Замечание. Если кривая расположена симметрично относительно некоторой прямой, то центр тяжести такой кривой находится на этой прямой.

Это замечание позволяет в некоторых случаях упростить нахождение координат центра тяжести плоской кривой.

Пример 1. Найти статический момент полуокружности относительно диаметра.

Решение. Выберем систему координат так, чтобы центр окружности совпал с началом координат, а диаметр, относительно которого мы ищем статический момент, совпал с осью . Тогда статический момент полуокружности относительно диаметра выразится формулой

В выбранной системе координат уравнение полуокружности запишется так: . Тогда

Пример 2. Найдем центр тяжести четверти окружности , расположенной в первом квадранте.

Решение. Данная кривая расположена симметрично относительна биссектрисы первого координатного угла, следовательно, центр тяжести этой кривой лежит на биссектрисе, а потому . Достаточно найти только .

Вычисление проще провести, перейдя к параметрическим уравнениям окружности. Так как ее радиус равен двум, то для четверти окружности имеем:

Отсюда находим, что и

Поскольку длина четверти данной окружности равна , то

Видео:Центр тяжести Метод дополненияСкачать

Вычисление статических моментов и координат центров тяжести плоских фигур

Найдем статический момент прямоугольника со сторонами и относительно стороны . Разобьем этот прямоугольник на элементарные прямоугольники, имеющие стороны и (рис. 61). Масса элементарного прямоугольника равна его площади (напомним, что по предположению плотность распределения массы равна единице). Поэтому элементарный статический момент равен , а статический момент всего прямоугольника равен

Теперь уже легко найти статический момент криволинейной трапеции, ограниченной сверху кривой , где — непрерывная и неотрицательная функция на отрезке , снизу осью абсцисс, а с боков прямыми .

Разобьем криволинейную трапецию на элементарные прямоугольники, основание каждого из которых равно и высота . Статический момент такого прямоугольника относительно оси абсцисс по формуле (1) равен , а потому статический момент всей криволинейной трапеции равен . В случае, когда не выполняется предположение о неотрицательности функции , эту формулу надо заменить такой:

(части фигуры, расположенные ниже оси абсцисс, дают отрицательный вклад в ).

Поскольку по предположению плотность равна единице, то масса криволинейной трапеции равна ее площади, т. е. интегралу , а потому ордината центра тяжести этой трапеции выражается формулой

Нетрудно найти и статический момент криволинейной трапеции относительно оси ординат. Для этого достаточно заметить, что расстояние элементарного прямоугольника от этой оси равно . Поэтому его статический момент равен , а статический момент всей трапеции выражается формулой

Пример 3. Найти статический момент (относительно оси ) фигуры, ограниченной осью абсцисс и одной аркой циклоиды:

Решение. Так как параметр одной арки циклоиды изменяется от до , то

Пример 4. Найти центр тяжести фигуры, ограниченной осью и одной полуволной синусоиды .

Решение. Так как фигура под полуволной синусоиды расположена симметрично относительно прямой , то центр тяжести лежит на этой прямой и, следовательно, . Ордината центра тяжести находится по формуле .

Итак, центр тяжести данной фигуры находится в точке .

Пример 5. Найти центр тяжести фигуры, ограниченной осью абсцисс и одной аркой циклоиды .

Решение. Данная фигура расположена симметрично относительно прямой , следовательно, центр тяжести ее находится на этой прямой, и потому . Найдем по формуле .

Площадь данной фигуры была вычислена раньше, она равна . Следовательно,

Центр тяжести данной фигуры находится в точке .

Видео:Найти центр и радиус окружностиСкачать

Координаты центра тяжести четверти окружности

1. Вычисление объема тела

Пусть функция f ( x ; y ) ≥ 0. Рассмотрим тело, ограниченное поверхностью z = f ( x ; y ), плоскостью z = 0 и цилиндрической поверхно­стью, образующие которой па­раллельны оси 0 z , а направ­ляющей служит граница об­ласти D . Как было показано выше, согласно формуле (6.3) объем данного тела равен

Пример 6.9. Вычислить объём тела, ограниченного параболоидом z = x 2 + y 2 + 1, плоскостью x + y –3=0 и координатными плоскостями.

Решение. Основанием тела служит треугольник ОАВ. Область D в данном случае определяется неравенствами:

2. Вычисление площади плоской фигуры

Если положить в формуле (6.18) f ( x , y )=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой h = 1. Объем такого цилиндра,

как известно, численно равен площади S основания D . Получаем формулу для вычисления площади S области D :

или, в полярных координатах,

Пример 6.10. Вычислить площадь фигуры, ограниченной прямой y = 2 x + 1 и параболой y = x 2 + 1.

Решение. Решая совместно систему

Применяя формулу (6.19), будем иметь:

Решение. Переходим к полярной системе координат, полагая x = r cos φ и y = r sin φ ; тогда получаем

3. Вычисление массы плоской фигуры (пластины)

Масса плоской пластинки D с переменной плотностью γ =γ ( x , y ) находится по формуле

4. Определение статических моментов и координат центра тяжести плоской фигуры

Статические моменты фигуры D относительно осей 0 x и 0 y могут быть вычислены по формулам

а координаты центра масс фигуры – по формулам

Статические моменты широко используются в сопротивлении материалов и других технических науках.

5. Определение моментов инерции плоской фигуры

Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т.е. . Моменты инерции плоской фигуры относительно 0 x и 0 y могут быть вычислены по формулам:

Момент инерции фигуры относительно начала координат – по формуле

Пример 6.12 . Найти массу, статические моменты и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом и координатными осями. Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.

Решение. По формуле (6.21) находим массу пластины. По условию, γ =γ ( x , y )= k ∙ xy , где k – коэффициент пропорциональности.Тогда

Находим статические моменты пластинки по формулам (6.22):

Находим координаты центра тяжести пластинки, используя формулы (6.23):

6. Поверхностный интеграл I рода

Обобщением двойного интеграла является поверхностный интеграл. Пусть в трехмерном пространстве О xyz в точках некоторой поверхности площади S определена непрерывная функция u = f ( x ; y ; z ). Разобьем поверхность на конечное число n частей S_i , площади которых равны ∆ S_i , а диаметры – d_i , . Выберем в каждой части S_i произвольную точку M_i ( x_i ; y_i ; z_i ) и составим сумму произведений вида

Она называется интегральной суммой для функции f ( x ; y ; z ) по поверхности S . Если при интегральная сумма (6.26) имеет предел, который не зависит ни от способа разбиения поверхности S, ни от выбора точек M_i ( x_i ; y_i ; z_i ), то он называется поверхностным интегралом I рода от функции f ( x ; y ; z ) по поверхности S и обозначается . Следовательно,

Теорема 6.3 (о существовании поверхностного интеграла). Если поверхность S гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция f ( x ; y ; z ) непрерывна на этой поверхности, то поверхностный интеграл существует

Формула (6.28)

выражает интеграл по поверхности S через двойной интеграл по проекции S на плоскость x 0 y . Отметим, что если поверхность S задана уравнением вида y=y(x;z) или x=x(y;z), то аналогично получим:

где D ₁ и D ₂ – проекции поверхности S на координатные плоскости xО z и y О z соответственно.

Пример 6.13. Вычислить , где S – часть цилиндрической поверхности , отсеченной плоскостями z = 0 и z = 3.

Решение . Из уравнения заданной цилиндрической поверхности выразим и учтём, что при x = 0 в плоскости x О y : . Так как частные производные равны , то согласно формуле (6.30), имеем

6.1. Площадь поверхности

Если поверхность S задана уравнением z = f ( x ; y ), a ее проекция на плоскость x 0 y есть область D , в которой z = f ( x ; y ), z_x ( x ; y ) и z_y ( x ; y ) – непрерывные функции, то ее площадь S вычисляется по формуле:

Пример 6.14. Вычислить площадь части плоскости x + y + z = 4, вырезаемой цилиндром x 2 + y 2 = 4 (рис. 6.10).

Чтобы вычислить этот интеграл, введём полярные координаты. Область D определяется: . Следовательно,

Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы γ =γ ( x ; y ; z ) . Все эти величины определяются одним и тем же способом:

– данную область разбивают на конечное число мелких частей;

– делают для каждой такой части предположения, упрощающие задачу;

– находят приближенное значение искомой величины;

– переходят к пределу при неограниченном измельчении разбиения области.

Проиллюстрируем описанный способ на примере определения массы материальной поверхности.

6.2. Масса поверхности

Пусть плотность распределения массы материальной поверхности есть γ =γ ( x ; y ; z ) . Для нахождения массы поверхности:

1. Разбиваем поверхность S на n частей S_i , , площадь которых обозначим ∆ S_i .

2. Выберем произвольную точку M_i ( x_i ; y_i ; z_i ) в каждой области S_i . Предполагаем, что в переделах области S_i плотность постоянна и равна её

4. Суммируя m_i по всей области, получаем: .

5. За точное значение массы материальной поверхности S принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей S_i , то есть

6.3. Моменты и центр тяжести поверхности. С татические моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по соответствующим формулам:

Пример 6.15. Вычислить координаты центра тяжести однородной поверхности параболоида z = x 2 + y 2 , ограниченной плоскостью z = 1.

Решение. Вершина заданного параболоида совпадает с началом координат. Так как поверхность однородная (постоянная плотность массы), то, основываясь на ее симметрии, можно сделать вывод, что центр тяжести расположен на оси 0 z . Тогда x_c = 0, y_c = 0 и по формуле (6.36) аппликата . Пересечем параболоид поверхностью z = 1, спроектируем линию пересечения на плоскость x 0 y – получим окружность x 2 + y 2 =1 в качестве области D . Вычислим элемент поверхности параболоида z = x 2 + y 2 по формуле (6.31), учитывая, что :

Аналогично, переходя к полярным координатам на плоскости x 0 y , получим:

📺 Видео

координаты центра тяжести треугольникаСкачать

Найдите центр тяжестиСкачать

Практическая работа по теме: Центр тяжестиСкачать

6.1. Центр тяжести линииСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Физика - движение по окружностиСкачать

Урок 79. Центр масс тела и методы определения его положенияСкачать

Центр тяжести фигуры. Способ 1Скачать

Техническая механика/Определение центра тяжести сложносоставного сечения (Это понятно?!))Скачать

Практическая №5 Определение центра тяжести сложной фигурыСкачать

Определение центра тяжести плоской фигуры. Подробное объяснение. Сопромат для чайниковСкачать

Центр тяжести дугиСкачать

№578. Найдите координаты центра и радиус сферы, заданной уравнением: а) х2+y2+z2 = 49; б) (x — 3)2Скачать