В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.
- Формула вычисления площади цилиндра
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
- Примеры задач
- Площадь поверхности цилиндра
- Как найти площадь поверхности цилиндра: боковую, основания, полную
- Площадь боковой поверхности цилиндра
- Круговой цилиндр
- Как рассчитать площадь боковой поверхности цилиндра с помощью калькулятора
- Примеры задач
- Осевое сечение прямого цилиндра
- Введите радиус основания и высоту цилиндра
- Площадь полной поверхности цилиндра
- Основные определения и свойства цилиндра
- Геометрическая фигура
- Осевое сечение наклонного цилиндра
- Примеры расчета площади поверхности цилиндра
- Площадь цилиндра формула через диаметр
- Площадь боковой поверхности цилиндра через радиус основания и высоту
- Заключение
- 🔥 Видео
Видео:11 кл.Егэ. Радиус основания цилиндра равен ,2 высота равна 3 .Найдите площадь боковой поверхности циСкачать

Формула вычисления площади цилиндра
1. Боковая поверхность
Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.
Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:
S = 2 π R h
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:
S = π R 2
Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:
3. Полная площадь
Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:
S = 2 π R h + 2 π R 2 или S = 2 π R (h + R)
Видео:Егэ,11 кл. Длина окружности основания цилиндра равна 3 , высота равна 2. Найдите площадь боковой повСкачать

Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .
Видео:Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндраСкачать

Площадь поверхности цилиндра
Площадь поверхности цилиндра. В этой статье мы рассмотрим задания связанные с площадью поверхности цилиндра . На блоге уже рассмотрены задания с таким телом вращения как конус. Цилиндр тоже относится к телам вращения. Что требуется и нужно знать о площади поверхности цилиндра? Давайте посмотрим на развёртку цилиндра:
Верхнее и нижнее основание это два равных круга:
Боковая поверхность это прямоугольник. При чём одна сторона этого прямоугольника равна высоте цилиндра, а другая длине окружности основания. Напомню, что длина окружности равна:
Итак, формула поверхности цилиндра:
*Учить эту формулу не нужно! Достаточно знать формулы площади круга и длины его окружности, тогда вы всегда сможете записать указанную формулу. Важно её понимание! Рассмотрим задачи:
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту и площадь поверхности цилиндра (считайте, что число Пи равно 3,14 и результат округлите до десятых).
Площадь полной поверхности цилиндра:
Даны длина окружности основания и площадь боковой поверхности цилиндра. То есть, нам дана площадь прямоугольника и одна его сторона, требуется найти другую сторону (это есть высота цилиндра):
Требуется радиус и тогда мы сможем найти указанную площадь.
Длина окружности основания равна трём, тогда запишем:
Округляем до десятых, получаем 7,4.
Ответ: h = 2; S = 7,4
Площадь боковой поверхности цилиндра равна 72Пи, а диаметр основания — 9. Найдите высоту цилиндра.
Площадь боковой поверхности цилиндра находится по формуле:
Площадь боковой поверхности цилиндра равна 64Пи, а высота — 8 . Найдите диаметр основания.
Площадь боковой поверхности цилиндра находится по формуле:
Найдём радиус основания и далее определим диаметр:
Диаметр равен двум радиусам, значит:
27058. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на Пи.
27133. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
27173. Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на Пи.
284361. Площадь боковой поверхности цилиндра равна 2Пи, а диаметр основания — 1. Найдите высоту цилиндра.
284362. Площадь боковой поверхности цилиндра равна 2Пи, а высота — 1. Найдите диаметр основания.
Будет ещё пару статей с цилиндрами, не пропустите!
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Как найти площадь поверхности цилиндра: боковую, основания, полную
Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать

Площадь боковой поверхности цилиндра
Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:
Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.
Формула площади осевого сечения цилиндра выводится из формулы расчета площади прямоугольника :
Видео:Видеоурок по математике "Цилиндр"Скачать

Круговой цилиндр
| V = πr 2 h = π | d 2 | h , |
| 4 |
где r – радиус основы, h – высота цилиндра, d – диаметр основы.
Видео:№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать

Как рассчитать площадь боковой поверхности цилиндра с помощью калькулятора
Калькулятор позволяет определить площадь цилиндра по одному из 2 вариантов исходных данных:
- внешний радиус и высота;
- внешний диаметр и высота.
Выберите соответствующий шаг и введите исходные данные в соответствующие поля.
Также важно указать единицы измерения по условиям задачи.
Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины площади.
Видео:Егэ.Длина окружности основания цилиндра равна 3 ,площадь боковой поверхности равна 6 .Найдите высотуСкачать

Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .
Видео:ЕГЭ БАЗА 16 номер Радиус основания цилиндра равен 15, а его образующая равна 14Скачать

Осевое сечение прямого цилиндра
Осевым называется любое сечение цилиндра, которое содержит его ось. Это определение означает, что осевое сечение будет всегда параллельно образующей линии.
В цилиндре прямом ось проходит через центр круга и перпендикулярна его плоскости. Это означает, что рассматриваемое сечение круг будет пересекать по его диаметру. На рисунке показана половинка цилиндра, которая получилась в результате пересечения фигуры плоскостью, проходящей через ось.
Не сложно понять, что осевое сечение прямого круглого цилиндра представляет собой прямоугольник. Его сторонами являются диаметр d основания и высота h фигуры.
Запишем формулы для площади осевого сечения цилиндра и длины hd его диагонали:
Прямоугольник имеет две диагонали, но обе они равны друг другу. Если известен радиус основания, то не сложно переписать эти формулы через него, учитывая, что он в два раза меньше диаметра.
Видео:2 задание ЕГЭ профиль стереометрияСкачать

Введите радиус основания и высоту цилиндра
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Площадь полной поверхности цилиндра формула:
S = Sбок + 2 Sосн 2 , где Sбок – площадь боковой поверхности, Sосн – площадь основания
или
S = 2 π R h + 2 π R 2 , где R – радиус оснований, h – высота цилиндра, π – число пи
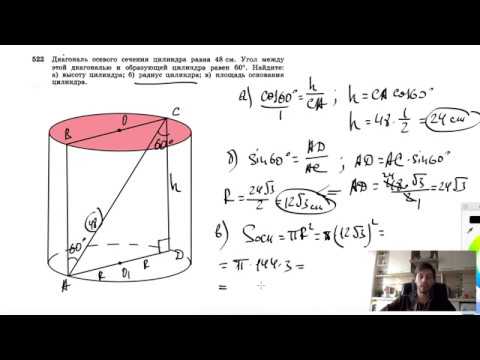
Видео:№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать
Площадь полной поверхности цилиндра
Для нахождения полной площади цилиндра нужно к полученной Sбок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле Sо = 2π * r2.
Конечная формула выглядит следующим образом:
Sпол = 2π * r2 + 2π * r * h.
Видео:ЗАДАНИЕ 2| ЕГЭ ПРОФИЛЬ| Высота конуса равна 30, а диаметр равен 32. Найдите образующую конуса.Скачать

Основные определения и свойства цилиндра
Рассмотрим две паралллельные плоскости паралллельные плоскости α и β и произвольную окружность радиуса r с центром в точке O , лежащую в плоскости α (рис. 1).
Если из каждой точки окружности опустить перпендикуляр на плоскость β , то основания этих перпендикуляров образуют на плоскости β окружность радиуса r , центр O1 которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).
 |
 |
 |
 |
 |
 |
 |













































