Утверждение, устанавливающее некоторое свойство и принимаемое без доказательства, называется .
Сколько прямых, параллельных данной прямой, можно провести через точку, не лежащую на данной прямой?
Выберите один из 4 вариантов ответа:
Верно ли утверждение: «Если прямая пересекает одну из параллельных прямых, то она пересекает и другую»?
Выберите один из 2 вариантов ответа:
Если прямая а параллельна прямой с и прямая b параллельная прямой с, то .
Выберите один из 3 вариантов ответа:
1) прямая а перпендикулярна прямой b
2) прямая а параллельна прямой b
3) прямые а и b пересекаются
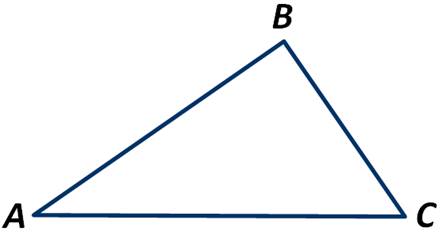
На рисунке изображён треугольник АВС. Сколько прямых, параллельных стороне ВС, можно провести через вершину А?
Выберите один из 4 вариантов ответа:
1) Нельзя провести ни одной параллельной прямой
2) Можно провести две параллельные прямые
3) Можно провести множество прямых, параллельных стороне ВС
4) Можно провести только одну параллельную прямую
Существует ли прямая, которая параллельна каждой из двух пересекающихся прямых?
Выберите один из 2 вариантов ответа:
2) Не существует
Если один из внутренних односторонних углов при параллельных прямых и секущей тупой, то какой второй угол?
Выберите один из 3 вариантов ответа:
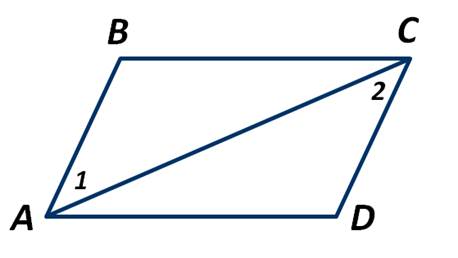
На рисунке угол 1 равен углу 2. Какие прямые являются параллельными?
Выберите один из 4 вариантов ответа:
1) BС параллельна СD
2) AB параллельна ВС
3) AD параллельна ВС
4) АВ параллельна СD
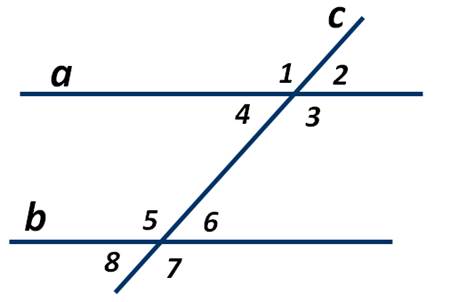
На рисунке при пересечении параллельных прямых а и b секущей с образовано восемь углов. Отметьте верные утверждения.
Выберите несколько из 4 вариантов ответа:
1) Угол 3 равен углу 5
2) Сумма углов 3 и 6 равна 180°
3) Угол 2 равен углу 7
4) Сумма углов 1 и 5 равна 180°
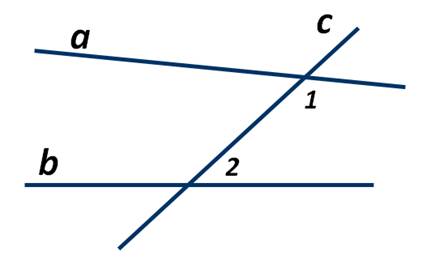
На рисунке угол 1 равен 125°, а угол 2 равен 60°. Как нужно изменить угол 1, чтобы прямая а была параллельна прямой b?
Выберите один из 4 вариантов ответа:
Видео:29. Теорема об углах, образованных двумя параллельными прямыми и секущейСкачать

Урок-практикум по геометрии в 7-м классе «Свойства углов, образованных при пересечении параллельных прямых секущей»
Разделы: Математика
Цели урока: (Слайд №1)
Образовательные: закрепление умений использовать знания признаков, свойств углов, образованных при пересечении параллельных прямых секущей, научить видеть различные способы при решении одной задачи.
Воспитательные: воспитание познавательной активности, чувства ответственности, культуры общения.
Развивающие: развитие логического мышления учащихся, внимания, активности, чувство ответственности, самостоятельности, культуры общения.
Тип урока: урок обобщения и систематизации знаний учащихся.
Организационные формы: парная, дифференцированно групповая.
Технология: уровневая дифференциация.
Структура урока:
- вводное слово учителя
- самостоятельная работа групп №2, №3
- актуализация знаний учащихся группы №1
- диктант
- тест
- самостоятельная работа группы №1
- защита у доски работ группами №2, №3
К данному уроку прилагается презентация (Приложение 1)
Ход урока:
Вводное слово учителя
Многие великие люди всех времен и народов говорили о значении математики. Не только ученые — математики, но и поэты, писатели, философы. Высказывание одного великого мыслителя: «ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства» Леонардо да Винчи (слайд №2).
Предметом исследования нашего урока будут углы, образованные при пересечении параллельных прямых секущей. Задачей нашего урока является обобщение и систематизация ваших знаний по данной теме.
В ходе групповой, парной, самопроверки вы еще раз закрепите знания свойств углов, образованных при пересечении параллельных прямых секущей (слайд №3).
Организация работы групп
- класс делится на 3 группы по уровню их обученности
- каждая группа получает определенные задания
- группа №3 — уровень «4-5». Решают по 3 задачи с последующей защитой у доски.
Выполняют в тетрадях и сдают учителю.Задания для групп с уровнем обученности «4-5»
Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать
Параллельность прямых
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).Видео:Параллельные прямые | Математика | TutorOnlineСкачать
Определение параллельности прямых
Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.
Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.
Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.
Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.
На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:Свойства углов, образованных двумя параллельными прямыми и секущей Задачи на признаки параллельностСкачать
Свойства и признаки параллельных прямых
Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.
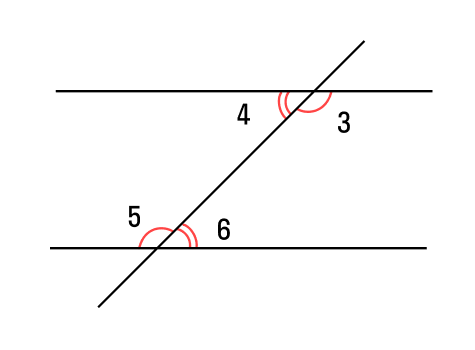
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.
Если секущая проходит через две параллельные прямые, то:
- два внутренних односторонних угла образуют в сумме 180°:
∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.
два внутренних накрест лежащих угла равны между собой:
два соответственных угла равны между собой:∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.
Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.
Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.
А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.
Задача 1
Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.
Решение
Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.
Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.
Задача 2
Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.
Решение
Поскольку а II b, значит ∠MKD + ∠KDN = 180°.
Соответственно, ∠MKD = 180° — ∠KDN = 180° — 150° = 30°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.
Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.
📽️ Видео
Углы, образованные при пересечении двух прямых секущейСкачать
Пары углов в геометрииСкачать
№203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать
Теоремы об углах, образованных двумя парал. прямыми и секущей | Геометрия 7-9 класс #30 | ИнфоурокСкачать
№208. Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50°Скачать
Теоремы об углах, образованных двумя параллельными прямыми и секущей.Скачать
Геометрия 7 класс. Теоремы об углах, образованных двумя параллельными прямымСкачать
№201. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210Скачать
Углы, образованные параллельными прямыми и секущейСкачать
Теоремы об углах, образованных двумя параллельными прямыми и секущей. Решение задач.Скачать
ГЕОМЕТРИЯ 7 класс : Соответственные, односторонние и накрест лежащие углыСкачать
УГЛЫ: Односторонние, Накрест Лежащие, Внутренние, Внешние // Теорема об углах — Геометрия 7 классСкачать
Это пора запомнить! Свойства углов при параллельных прямых и секущей. #геометрияСкачать
7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать
29 Теоремы об углах, образованных двумя параллельными прямыми и секущей - Геометрия 7-9 АтанасянСкачать
Самостоятельная работа | Геометрия 7 класс | Теоремы об углах образованных параллельными прямымиСкачать