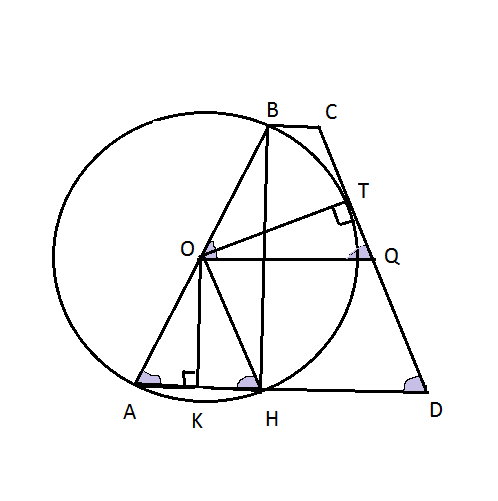
Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC = 1.
а) Треугольник AOH равнобедренный и трапеция ABCD равнобедренная, поэтому ∠AHO = ∠OAH = ∠CDA. Значит, прямые OH и CD параллельны, а так как OQ — средняя линия трапеции, то параллельны прямые OQ и AD. Противоположные стороны четырёхугольника DQOH попарно параллельны, следовательно, DQOH — параллелограмм.
б) Пусть окружность с центром в точке O радиуса R касается стороны CD в точке P. В прямоугольных треугольниках OPQ и AHB имеем
Пусть AH = x. Поскольку трапеция ABCD равнобедренная, AD = 2AH + BC; DH = AH + BC = x + 1. Тогда
откуда x = 1. Значит, AD = 2x + 1 = 3.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:№644. Прямые МА и MB касаются окружности с центром О в точках А и В. Точка С симметрична точке ОСкачать  Задача 11237 .Условие
Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD. а) Докажите, что четырёхугольник DQOH — параллелограмм. б) Найдите AD, если ∠BAD=60° и BC=2. Решение
а) б)Δ OAH — равносторонний, углы при основании 60 градусов ⇒ АН=R ⇒ AK=KH=R/2 Δ ОАК подобен Δ OTD OQ- cредняя линия трапеции АВСD. OQ=(BC+AD)/2=(2+2+2R)/2=2+R Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать  Вписанная в равнобедренную трапецию окружностьКакими свойствами обладает вписанная в равнобедренную трапецию окружность? 1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.
И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность. Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:
2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.
3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.
Из прямоугольного треугольника ABF по теореме Пифагора
4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство
5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.
6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.
📹 Видео№676. Стороны угла А касаются окружности с центром О радиуса r. Найдите: а) ОА,Скачать  Как найти стороны равнобокой трапеции, описанной около трёх попарно касающихся равных окружностей?Скачать  Трапеция. Практическая часть - решение задачи. 8 класс.Скачать  ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать  ЕГЭ задание 16 Площадь трапецииСкачать  Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать  Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  8 класс, 6 урок, ТрапецияСкачать  ЕГЭ Задание 16 Равнобедренная трапеция Вписанные окружностиСкачать  Боковая сторона равнобедренной трапеции равна ее меньшему основаниюСкачать  Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть II)Скачать  Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать  №599. Найдите площадь равнобедренной трапеции с основаниями 2 см и 6 см, если уголСкачать  Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать  Задание 25_Признак равнобедренной трапецииСкачать  Как доказать У равнобедренной трапеции углы при основаниях равны и диагонали равныСкачать  9.56.1. Планиметрия. Гордин Р.К.Скачать  ЕГЭ Задание 16 Трапеция и две окружностиСкачать  |
То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
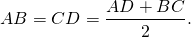
Если MN —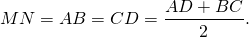
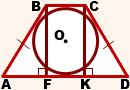По свойству равнобедренной трапеции,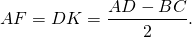
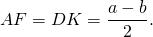
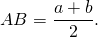
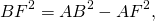
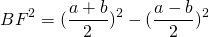
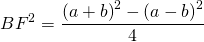
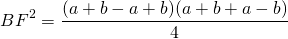
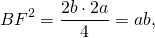
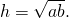
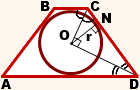Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,