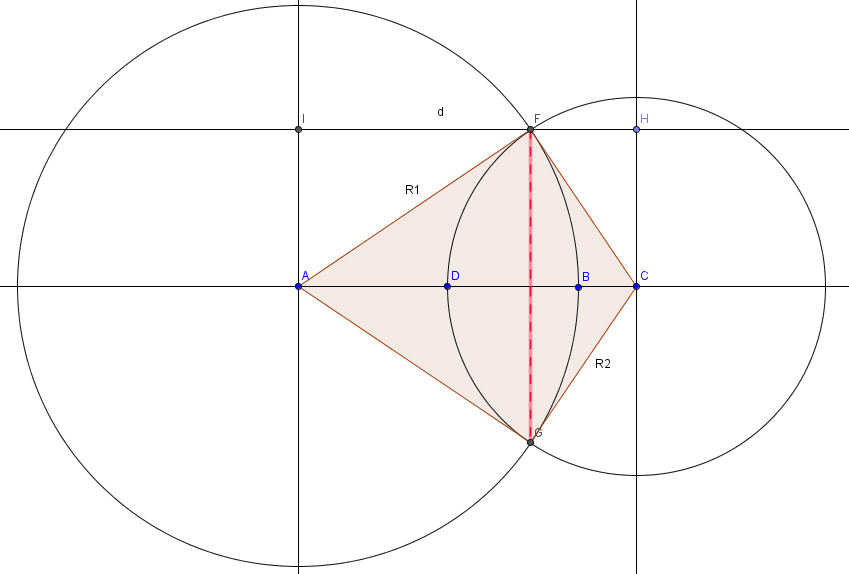
Позволяет рассчитать площадь пересечения двух окружностей произвольных радиусов.
Используются достаточно простые формулы, которые элементарно доказываются.
Дополнительно есть калькулятор, который высчитывает координаты пересечения двух окружностей
Площадь пересечения двух окружностей состоит из двух сегментов FDG и FBG
Вывести формулу расчета площади пересечения двух окружностей можно из двух общеизвестных формул и знаний решения треугольника:
Формулы сектора окружности
и длина хорды окружности
По известным сторонам треугольника AFС определяем высоту на сторону AC.
Удвоением этой высоты мы получаем длину хорды, после этого узнаем угол альфа по второй формуле.
По известным сторонам треугольника AFG узнаем его площадь. Вычитаем её из площади сектора окружности, ведь угол альфа нам уже известен.
И получаем площадь сегмента FBG
Подобным образом вычисляем FDG
Это лишь один из способов решения задачи вычисления площади пересечения двух окружностей.
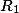
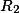
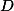
- Пример
- Расчет площади пересечения окружностей методом Монте-Карло
- Обоснование
- Реализация задачи на JavaScript
- Пара гвоздей в метод Бутстрапа
- Площадь кольца
- Онлайн калькулятор
- Площадь кольца по радиусам или диаметрам
- Площадь кольца по толщине и любому другому параметру
- Теория
- Площадь кольца через радиусы
- Формула
- Пример
- Площадь кольца через диаметры
- Формула
- Пример
- Площадь кольца через толщину
- Формулы
- Пример
- 🌟 Видео
Видео:Геометрия 9 класс (Урок№10 - Взаимное расположение двух окружностей.)Скачать

Пример
Хотим узнать площадь пересечения двух окружностей радиусом в 1 и расстоянием между центрами 0.8079455
Пишем okr 1 1 0.8079455
Площадь двух пересекающихся окружностей равна = 1.5707963388681
Первая окружность радиус 4, вторая окружность радиус 2, расстоянием между центрами 3
Пишем okr 4 2 3
Площадь двух пересекающихся окружностей равна = 9.5701994729833
Первая окружность радиус 4, вторая окружность радиус 2, расстоянием между центрами 0
Видео:9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

Расчет площади пересечения окружностей методом Монте-Карло

Итак, моя задача заключалась в необходимости вычисления площади фигуры, являющейся пересечением окружностей, с последующей реализацией на языке JavaScript. Площадь под графиком – это интеграл. Интегрирование методом Монте-Карло достаточно широко известно, но, как многие верно заметят, его применение требует некоторого обоснования. За подробностями прошу под кат.
Обоснование
Задача расчета площади пересечения двух окружностей является тривиальной геометрической задачей (координаты центров окружностей и их радиусы нам известны). Площадь пересечения двух окружностей – это сумма площадей соответствующих сегментов этих окружностей. Есть решения для расчета площади пересечения двух, трех, четырех окружностей в различных частных случаях.
А вот решения общего случая для пересечения даже трех окружностей уже далеко не так тривиальны. В процессе поиска я нашел даже исследования по расчету площади пересечения N окружностей, однако они настолько же интересны, насколько и сложны.
Здесь на сцену выходит метод Монте-Карло. Благодаря современным компьютерным мощностям этот метод позволяет провести большое количество статистических испытаний, на основе результатов которых делается обобщение.
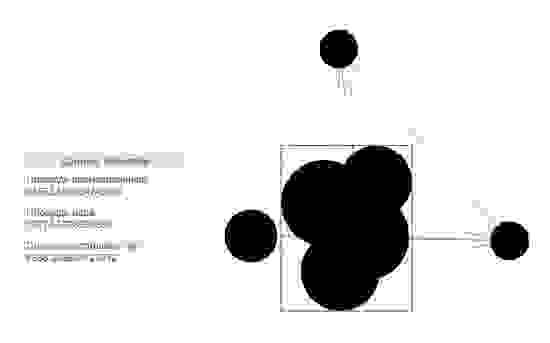
Итак, алгоритм расчета площади любой фигуры методом Монте-Карло сводится к следующему:
- Фигура вписывается в прямоугольник. Координаты сторон прямоугольника известны, значит, известна его площадь.
- Псевдослучайным образом внутри прямоугольника генерируется большое количество точек. Для каждой точки определяется, попала ли точка внутрь исходной фигуры или нет.
- В результате площадь исходной фигуры вычисляется исходя из обычной пропорции: отношение количества точек, попавших в фигуру, к общему количеству сгенерированных точек равно отношению площади фигуры к площади ограничивающего ее прямоугольника.
Последняя проблема, которую надо решить, заключается в том, что каким-то образом необходимо определять, попала ли точка внутрь исходной фигуры. В моем случае данная задача решается достаточно просто, поскольку моя фигура состоит из окружностей, координаты центров и радиусы которых известны.
Реализация задачи на JavaScript
Пара гвоздей в метод Бутстрапа
Если говорить именно о методе Бутстрапа, то мое личное мнение заключается в том, что случайная генерация набора данных по имеющемуся набору в общем случае не может служить для оценки закономерностей, поскольку сгенерированная информация не является достоверной. В общем, это же, только более умными (и нередко более резкими) словами, говорят и многие авторы, например, Орлов в своем учебнике по Эконометрике.
Видео:Найти площадь пересечения кругов. Задача для тех, кто учился в школе на пятеркиСкачать

Площадь кольца
Видео:Пересечение двух окружностейСкачать

Онлайн калькулятор
Площадь кольца по радиусам или диаметрам

у внешней окружности
у внутренней окружности
Площадь кольца по толщине и любому другому параметру

толщина кольца t =
Видео:Взаимное расположение окружностей. 7 класс.Скачать

Теория
Площадь кольца через радиусы
Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?
Формула
Пример
К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:
S = 3.14 ⋅ (3² — 2²) = 3.14 ⋅ (9 — 4) = 3.14 ⋅ 5 = 15.7 см²
Ответ: S = 15.7 см²
Площадь кольца через диаметры
Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?
Формула
Пример
К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:
S = 3.14 / 4 ⋅ (4² — 2²) = 0.785 ⋅ (16 — 4) = 9.42 см²
Ответ: S = 9.42 см²
Площадь кольца через толщину
Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:
- внешний диаметр D
- внутренний диаметр d
- радиус внешней окружности R
- радиус внутренней окружности r
Формулы
Пример
Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:
S = 3.14/4 ⋅ (5² — (5 — 2 ⋅ 2)²) = 0.785 ⋅ (25 — 1) = 18.84 см²
🌟 Видео
Теорема о числе точек пересечения двух окружностейСкачать

Взаимное расположение двух окружностей. Урок 8. Геометрия 9 классСкачать

Пересечение двух окружностейСкачать

Геометрия В точках пересечения двух окружностей с радиусами 4 и 8 см касательные к ним взаимноСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

1 2 4 сопряжение окружностейСкачать

Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать

№675. Стороны угла О касаются каждой из двух окружностей, имеющих общую касательную в точке АСкачать
Внешнее сопряжение двух окружностейСкачать
Взаимное расположение окружностей. Практическая часть. 7 класс.Скачать

Геометрия 16-09. Взаимное расположение двух и более окружностей. Задача 9Скачать

Геометрия Общая хорда двух окружностей служит для одной из них стороной вписанного квадрата, а дляСкачать

Алгоритмы. Пересечение окружностейСкачать

На каждой из двух окружностей с радиусами 3 и 4 лежат по три вершины ромба. Найдите его сторону.Скачать

Взаимное расположение окружностей. Точки пересечения окружностейСкачать