Построение биссектрисы равнобедренного треугольника

В данной публикации мы рассмотрим основные свойства биссектрисы равнобедренного треугольника (внутренней и внешней), а также разберем пример решения задачи по данной теме.

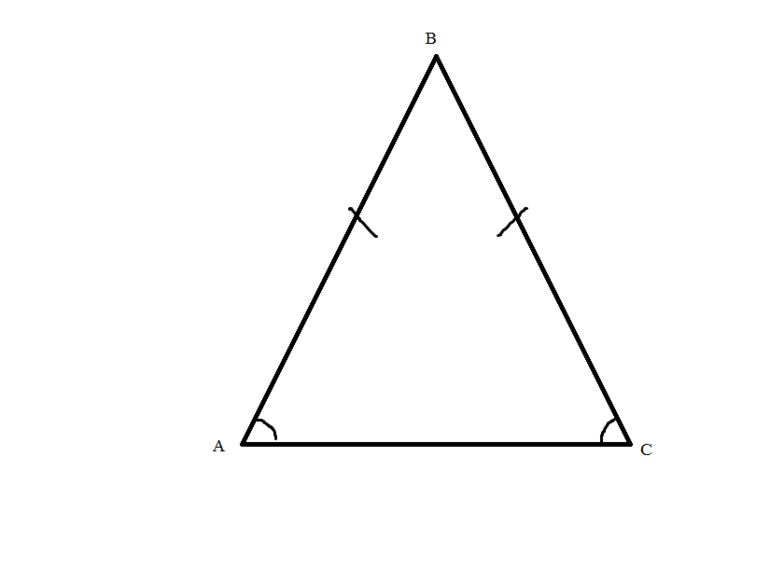
Примечание: напомним, что равнобедренным называется треугольник, в котором две стороны равны (боковые), а третья является основание фигуры.

Видео:Построение биссектрисы в треугольникеСкачать

Свойства биссектрисы равнобедренного треугольника

Свойство 1

В равнобедренном треугольнике биссектрисы, проведенные к боковым сторонам, равны между собой.

• AB = BC, т.к. являются боковыми сторонами равнобедренного △ABC;
• AF = CG, т.к. это биссектрисы, проведенные к боковым сторонам треугольника (или биссектрисы углов BAC и ACB, которые также равны между собой).

Обратная формулировка: если две из трех биссектрис в треугольнике равны, значит он является равнобедренным.

Свойство 2

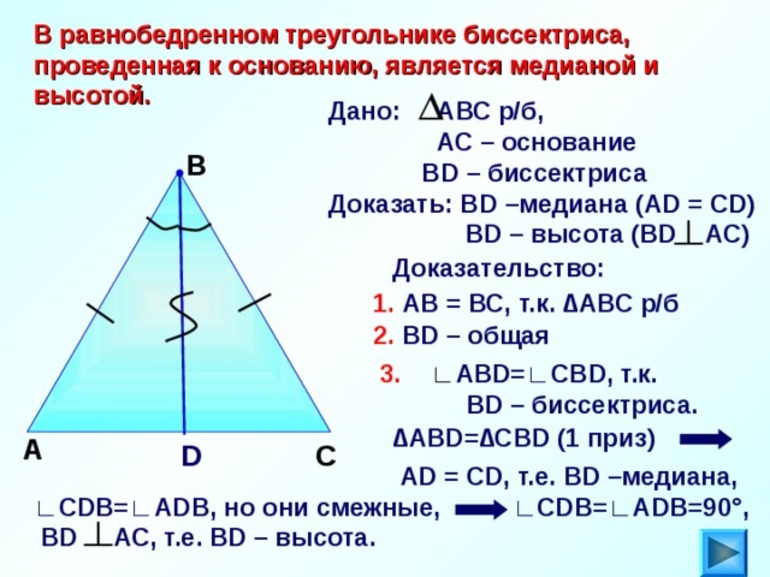
В равнобедренном треугольнике биссектриса, проведенная к основанию, одновременно является и медианой и высотой.

• BH – биссектриса угла ABC, проведенная к основанию AC;
• BH – медиана, значит она делит AC пополам, т.е. AH = HC;
• BH – высота, следовательно, она перпендикулярна AC.

Свойство 3

Если известны стороны равнобедренного треугольника, то длину биссектрисы, проведенную к основанию, можно посчитать по формуле:

Примечание: данная формула следует из теоремы Пифагора ( l и a – катеты прямоугольного треугольника, b – его гипотенуза).

Свойство 4

Внешняя биссектриса угла равнобедренного треугольника, расположенного напротив его основания, параллельна этому основанию.

• BD – внешняя биссектриса ∠ABC треугольника;
• BD параллельна основанию AC.

Примечание: к равнобедренному треугольнику применимы и другие свойства биссектрисы, приведенные в нашей публикации – “Определение и свойства биссектрисы угла треугольника”.

Видео:Построение биссектрисы угла. 7 класс.Скачать

Пример задачи

Биссектриса равнобедренного треугольника с боковой стороной 25 см равняется 20 см. Найдите периметр фигуры.

Решение
Воспользуемся формулой, приведенной в Свойстве 3, чтобы найти длину основания.
a 2 = b 2 – l 2 = 25 2 – 20 2 = 225 .

Извлекаем квадратный корень из найденного значения и получаем 15 см.
Следовательно, основание треугольника равно 30 см (15 см ⋅ 2).

Периметр фигуры равен сумме всех ее сторон, т.е.: 25 см + 25 см + 30 см = 80 см.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Как можно построить биссектрису угла с помощью циркуля и линейки?

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Процесс построения

Биссектриса (лат. bisectio) представляет собой геометрическое место точек внутри угла (острый, прямой или тупой), которые одинаково удалены от обеих его сторон.

Для её построения нужно подготовить различные школьные принадлежности и выполнить несколько простых действий.

Подготовительный этап

Чтобы быстро найти биссектрису треугольника с помощью циркуля, нужно провести тщательную подготовку. Она заключается в поиске школьных принадлежностей, которые будут использоваться при построении.

Необходимые предметы:

Порядок действий

Нарисовать луч, разделяющий пополам угол, можно при помощи транспортира. Однако если этой школьной принадлежности нет в наличии, заменить её сможет обыкновенный циркуль.

Быстрый способ:

1. На листе бумаги рисуют 2 пересекающиеся линии.
2. Чтобы построить биссектрису данного угла, в его вершину ставят ножку циркуля и чертят окружность произвольного радиуса.
3. Отмечают точками места пересечения сторон угла с окружностью.
4. На них поочерёдно ставят циркуль и, не меняя радиус, рисуют 2 дуги.
5. Находят и отмечают место их пересечения.
6. Стирают дуги ластиком, чтобы они не мешали дальнейшей работе.
7. С помощью линейки и простого карандаша проводят искомый отрезок, соединяющий вершину угла с точкой пересечения дуг.

С помощью циркуля можно легко найти биссектрису треугольника (всякого). Для этого понадобится стандартный набор школьных принадлежностей и наличие базовых знаний геометрии.

Порядок действий:

1. Любым известным способом вписывают окружность в треугольник.
2. С помощью карандаша и линейки из её центра проводят линии к каждой вершине.
3. Полученные отрезки станут частью искомого луча.

Видео:Построение медианы в треугольникеСкачать

Альтернативный вариант

Если у ученика нет циркуля, то начертить луч, разделяющий угол пополам, можно и без этой школьной принадлежности. Для работы понадобится линейка, карандаш и транспортир.

Правильная последовательность действий:

1. Нулевое значение на шкале прикладывают к вершине.
2. Совмещают линейку транспортира с одним из лучей и определяют величину угла.
3. Полученное значение делят пополам.
4. Затем заново прикладывают транспортир и откладывают величину, полученную в результате расчётов.
5. Через эту точку и вершину проводят отрезок, который будет являться искомым лучом.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Полезные советы

В некоторых случаях для нахождения не нужно использовать транспортир и циркуль. Это возможно только тогда, когда нужно определить расположение биссектрисы в треугольнике.

Полезные рекомендации:

1. Биссектриса всегда разделяет противолежащую сторону треугольника в отношении, равном пропорции 2 других сторон геометрической фигуры.
2. В равнобедренном треугольнике биссектрисы всегда пересекаются под прямым углом.
3. Если треугольник равносторонний, то все биссектрисы будут параллельны противоположным сторонам. При этом длина образованных отрезков будет одинаковой.

Построить биссектрису угла с помощью циркуля сможет даже двоечник. Для этого ему понадобится минимум времени, знаний и усилий. Подробно изучив порядок действий, каждый учащийся сможет легко поделить любой угол пополам и объяснить этот процесс одноклассникам.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Please wait.

Видео:Построение высоты равнобедренного треугольника с помощью циркуля и линейкиСкачать

We are checking your browser. mathvox.ru

Видео:Построение биссектрисы углаСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d4c87a65d360c48 • Your IP : 85.95.179.65 • Performance & security by Cloudflare

🎦 Видео

ПОСТРОЕНИЕ БИССЕКТРИСЫ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКА. ЗАДАЧИ НА ПОСТРОЕНИЕ | ГЕОМЕТРИЯ 7 классСкачать

Построение высоты в треугольникеСкачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

Построение биссектрисы углаСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Равнобедренный треугольник. 7 класс.Скачать

Свойство биссектрисы равнобедренного треугольникаСкачать

Геометрия. 7 класс. Теоремы. Т6. Второе свойство равнобедренного треугольника.Скачать

Свойства равнобедренного треугольника. 7 класс.Скачать