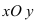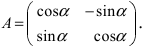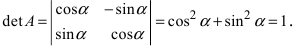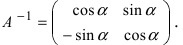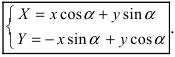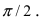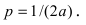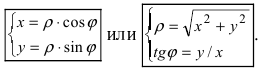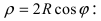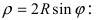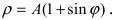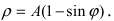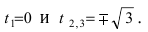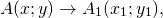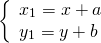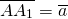Образ окружности на вектор

Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Ваш ответ

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,882
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Уравнение окружности (1)Скачать

Как перенести окружность на вектор

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Окружность в параллельном переносе

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Преобразования декартовой системы координат с примерами решения

Содержание:

Видео:Физика - движение по окружностиСкачать

Преобразования декартовой системы координат

Параллельный перенос и поворот системы координат

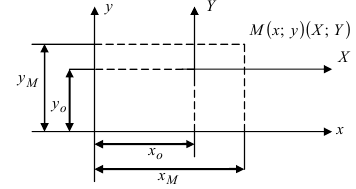
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):

Рис. 46. Параллельный перенос одной системы координат относительно другой системы.

Систему координат

Пример:

Дана точка М(3;2) и начало новой системы координат 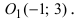Вычислить положение точки М в новой системе отсчета.

Решение:

Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим 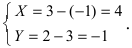Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).

2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 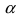(Рис. 47):

Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.

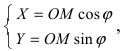
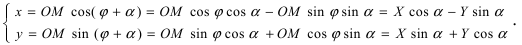
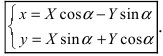
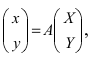
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны а координаты этой точки в старой системе координат равны Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид В матричном виде эти равенства можно записать в виде где матрица перехода

Найдем обратное преобразование системы координат, найдем матрицу 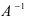обратную к матрице А:

Найдем алгебраические дополнения всех элементов

Запишем обратную матрицу

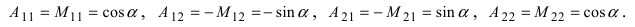
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.

Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.

Таким образом, имеем 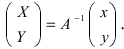Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:

Пример:

Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол

Решение:

Воспользуемся полученными формулами 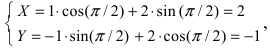т.е. в новой системе координат точка имеет координаты М(2; -1).

Рассмотрим применение преобразования координат:

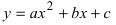
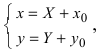
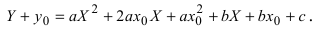
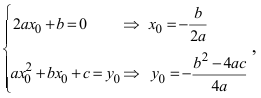
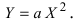
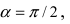
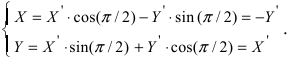
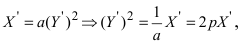
а) Преобразовать уравнение параболы к каноническому виду. Проведем параллельный перенос системы координат получим Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства тогда уравнение принимает вид Выполним поворот системы координат на угол тогда Подставим найденные соотношения в уравнение параболы где параметр параболы

Пример:

Преобразовать уравнение параболы 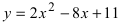к каноническому виду.

Решение:

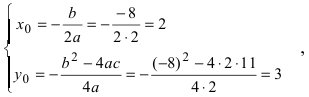
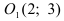
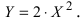
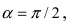
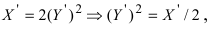
Найдем начало отсчета новой системы координат после параллельного переноса т.е. точка — начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид Проведем поворот системы отсчета на угол тогда

следовательно, параметр параболы р = 1/4.

б) Выяснить, какую кривую описывает функция

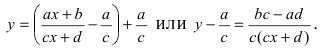
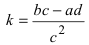
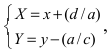
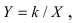
Проведем следующее преобразование Производя параллельный перенос системы координат, вводя обозначение

и новые координаты получим уравнение которое описывает равнобочную гиперболу.

Полярные координаты. Замечательные кривые

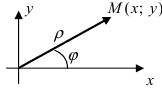
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 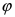между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).

Рис. 48. Полярная система координат.

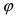
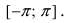
Главными значениями угла являются значения, лежащие в интервале Из рисунка видно, что декартовы и полярные координаты связаны формулами

Рассмотрим замечательные кривые в полярной системе координат:

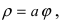
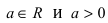
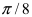
1. Спираль Архимеда где число (Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу и на каждом луче отложим ему соответствующее значение р.

Рис. 49. Спираль (улитка) Архимеда.

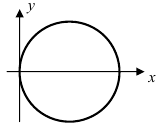
2. Уравнение окружности: уравнение 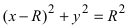описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид

Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.

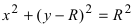
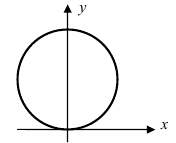
3. Уравнение описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид

Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.

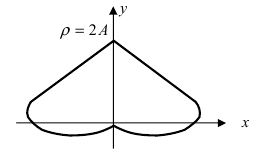
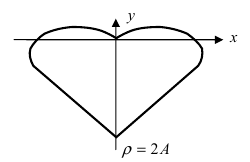
4. Кардиоиды:

Рис. 52. Кардиоида

Рис. 53. Кардиоида

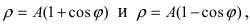
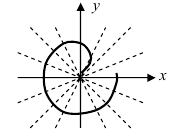
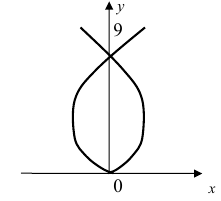
Аналогично выглядят кардиоиды но они вытянуты вдоль оси абсцисс Ох.

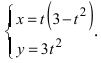
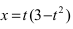
5. Петля: Величина равна нулю при

Для первого корня у = 0, а для второго и третьего — у = 9 . Следовательно, петля имеет вид

• Бесконечно малые и бесконечно большие функции
• Замечательные пределы
• Непрерывность функций и точки разрыва
• Точки разрыва и их классификация
• Экстремум функции
• Методы решения систем линейных алгебраических уравнений (СЛАУ)
• Скалярное произведение и его свойства
• Векторное и смешанное произведения векторов

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Длина вектора через координаты. 9 класс.Скачать

Параллельный перенос

Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.

Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.

1) Введём на плоскости декартовы координаты x, y.

Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.

Формулы параллельного переноса

Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1)

то параллельный перенос задаётся формулами:

Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.

2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:

Свойства параллельного переноса

1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).

2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).

4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.

В алгебре параллельный перенос широко используется для построения графиков функций.

Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Метод параллельного переноса

Перейдем сразу к решению задач на построение методом параллельного переноса.

Задача 6.34. Даны две окружности F_v F₂ и прямая I. Провести прямую, параллельную прямой I, на которой окружности F_r и F₂ высекают равные хорды.

Пусть прямая V искомая, т.е. прямая V высекает на данных окружностях равные хорды АВ иА’В’ (рис. 6.34).

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Параллельный перенос

Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.

Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.

1) Введём на плоскости декартовы координаты x, y.

Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.

Формулы параллельного переноса

Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1)

то параллельный перенос задаётся формулами:

Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.

2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:

Свойства параллельного переноса

1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).

2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).

4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.

В алгебре параллельный перенос широко используется для построения графиков функций.

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Геометрия. 9 класс

Конспект
Отметим точки A, B и зададим некоторый вектор а. Отложим вектор а от каждой из точек. При этом точка А отображается в точку А₁, точка В отображается в точку В₁. Таким образом вектор АА₁ равен вектору ВВ₁ и равны вектору а. Этот вид отображения плоскости на себя называется параллельным переносом.

Проведем отрезок АВ. Отложим вектор р от точек А и В. При этом точка А отображается в точку А₁, точка В отображается в точку В₁. Проведем отрезок А₁В₁. Отрезок АВ отображается на отрезок А₁В₁ при параллельном переносе на вектор р.

Построим треугольник ABC и задаем некоторый вектор а. Отложим вектор р от каждой из точек А, В, С. При этом точка А отображается в точку А₁, точка В отображается в точку В₁, точка С отображается в точку С₁. Таким образом векторы АА₁ = ВВ₁ = СС₁ и равны вектору а. Соединим отрезками точки А₁, В₁, С₁. Треугольник АВС отображается на треугольник А₁В₁С₁ при параллельном переносе на вектор а.
Сформулируем определение. Параллельным переносом на вектор р называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что вектор ММ₁ = р. Является ли параллельный перенос движением – отображением плоскости на себя, сохраняющим расстояние?

Пусть при параллельном переносе на вектор а точки M и N отображаются в точки M₁ и N₁. Так как вектор MM₁ равен вектору a и вектор NN₁ равен вектору a, то векторы MM₁ и NN₁ равны, т.е. MM₁ = NN₁, MM₁ ║ NN₁ следовательно, четырехугольник – параллелограмм, т.е. MN = M₁N₁. Значит, расстояние не изменяется. Таким образом доказали, что параллельный перенос является движением. Отметим следующие свойства.
При параллельном переносе:
1) отрезок переходит в равный ему отрезок;

2) угол переходит в равный ему угол;

3) окружность переходит в равную ей окружность;

4) любой многоугольник переходит в равный ему многоугольник;

5) параллельные прямые переходят в параллельные прямые;

6) перпендикулярные прямые переходят в перпендикулярные прямые.

Чтобы задать параллельный перенос достаточно задать некоторый вектор т.е. указать направление и расстояние.

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Составьте уравнение образа окружности x ^ 2 + y ^ 2 — 2x — 4y — 12 = 0 при параллельном переносе на вектор a ?

Математика | 5 — 9 классы

Составьте уравнение образа окружности x ^ 2 + y ^ 2 — 2x — 4y — 12 = 0 при параллельном переносе на вектор a .

(х ^ 2 + 1) + (y ^ 2 + 3) — (2x + 1) — (4y + 3) — 12 + 4 = 4.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Дана окружнасть s радиуса 1 с центром в начале координат?

Дана окружнасть s радиуса 1 с центром в начале координат.

Найдите центр и уравнение окружности , в которую переходит окружность s при параллельном переносе вдоль оси Ox.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Составе уравнение прямой, проходящей через точку А( — 1 ; 3) параллельно вектору s = ?

Составе уравнение прямой, проходящей через точку А( — 1 ; 3) параллельно вектору s = ?

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Точки М(1 ; 5)и N( — 7 ; 1)задают концы диаметра окружности?

Точки М(1 ; 5)и N( — 7 ; 1)задают концы диаметра окружности.

Найти параллельный перенос, при котором центр данной окружности переходит в точку А»( — 5 ; — 3).

Запишите уравнение полученной окружности.

Видео:Как разложить вектор по базису - bezbotvyСкачать

Составьте уравнение окружности с центром в начале координат и радиусом 12 см?

Составьте уравнение окружности с центром в начале координат и радиусом 12 см.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Составьте уравнение образа окружности x2 + y2 + 6x – 8y – 11 = 0?

Составьте уравнение образа окружности x2 + y2 + 6x – 8y – 11 = 0.

При повороте на 180 градусов против часовой стрелки относительно начало координат.

Видео:Построение проекции вектора на осьСкачать

Образом точки А( — 3 ; 6) при параллельном переносе является точка А1 (7 ; 2)?

Образом точки А( — 3 ; 6) при параллельном переносе является точка А1 (7 ; 2).

Найдите образ точки B( — 1 ; 8).

Видео:Составить уравнение образа окружности при осевой и центральной симметрии. Геометрия 9 классСкачать

Начертите треугольник РНО?

Начертите треугольник РНО.

Постройте точку М, в которую отобразится точка Р при параллельном переносе на вектор НО.

Видео:ДВИЖЕНИЕ ПО ОКРУЖНОСТИ 9 класс физика ПерышкинСкачать

Образом точки А(7 ; — 4) при параллельном переносе является точка А1(1 ; 3)?

Образом точки А(7 ; — 4) при параллельном переносе является точка А1(1 ; 3).

Найдите образ точки.

Видео:векторСкачать

Составьте уравнение окружности с центром О ( — 4 ; 2) и радиусом 3?

Составьте уравнение окружности с центром О ( — 4 ; 2) и радиусом 3.

Составить уравнение прямой проходящей через точку М (0, 2, 3) параллельно вектору s = (1, — 2, 3)?

Составить уравнение прямой проходящей через точку М (0, 2, 3) параллельно вектору s = (1, — 2, 3).

На этой странице сайта размещен вопрос Составьте уравнение образа окружности x ^ 2 + y ^ 2 — 2x — 4y — 12 = 0 при параллельном переносе на вектор a ? из категории Математика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 — 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.