Нормальная составляющая вектора индукции (5 видео)

Граничные условия для векторов электрического и магнитного поля на границе раздела двух сред

А) Граничные условия для вектора электрической индукции.

Рассмотрим границу раздела двух сред с различными диэлектрическими проницаемостями и . Выделим на границе элементарный цилиндр, как показано на рис. 3.1.1.

Нормальная составляющая вектора индукции

Рис.1.4.1.Элементарный цилиндр, выделенный на границе раздела двух сред для определения граничных условий на вектор электрической индукции. и — нормали к поверхности S.

Согласно теореме Гаусса-Остроградского поток вектора электрической индукции через замкнутую поверхность S равен алгебраической сумме зарядов внутри объема V, ограниченного этой поверхностью:

(3.1.1)

Устремим высоту цилиндра к нулю . Тогда (3.1.1) преобразуется так:

(3.1.2)

Где , – компоненты вектора индукции, перпендикулярные границе раздела, S — площадь основания цилиндра.

Введем поверхностную плотность заряда:

(3.1.3)

Размерность поверхностной плотности заряда = Кл/м2 (Кулон на квадратный метр).

Тогда (3.1.2) можно переписать в виде

(3.1.4)

Если плотность поверхностного заряда равна нулю (), то

. (3.1.5)

Мы можем сформулировать следующее важное утверждение:

На границе раздела, не содержащей поверхностных зарядов, нормальная составляющая вектора электрической индукции непрерывна.

Б) Граничные условия для вектора магнитной индукции.

Рассмотрим границу раздела двух сред, обладающих различной магнитной проницаемостью. Из тех же соображений, что и в предыдущем пункте и принимая во внимание, что магнитных зарядов не существует, можно записать

(3.1.6)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред нормальная составляющая вектора магнитной индукции всегда непрерывна.

В) Граничные условия для вектора напряженности электрического поля .

Рассмотрим снова границу раздела двух сред с различными диэлектрическими проницаемостями и . Выделим на границе замкнутый контур в соответствии с рис. 3.1.2. и используем закон электромагнитной индукции:

Где L — выбранный контур, L = 2 (1 + ) , S — площадь поверхности, ограниченная контуром L.

Рис.3.1.2. Контур на границе раздела двух сред, используемый при определении граничных условий для векторов напряженности электрического поля.

Устремим ширину контура к нулю, тогда поток вектора через поверхность S обратится в ноль, и мы получим

(3.1.7)

Откуда следует, что

(3.1.8)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред касательная составляющая вектора напряженности электрического поля всегда непрерывна.

Г) Граничные условия для вектора напряженности магнитного поля Н.

Как в предыдущем случае выделим на границе раздела двух сред замкнутый контур L (рис.1.4.2). Воспользуемся законом полного тока

(3.1.9)

Где — плотность тока, протекающего через поверхность S, ограниченную контуром L.

Учтем, что вдоль границы раздела может течь ток проводимости, тогда при стремлении следует ввести поверхностную плотность тока:

(3.1.10)

Размерность поверхностной плотности тока [] = А/м. Теперь (3.1.9) можно переписать так:

Откуда следует, что

(3.1.11)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред разность касательных составляющих напряженности магнитного поля равна поверхностной плотности тока.

При отсутствии поверхностного тока

(3.1.12)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред, по которой не течет поверхностный ток, касательная составляющая магнитного поля непрерывна.

Д) Граничные условия на поверхности идеального проводника.

Определим идеальный проводник, как проводник, внутрь которого не может проникать электромагнитное поле . Для полей СВЧ-диапазона хорошие проводники (серебро, медь) можно в первом приближении рассматривать как идеальные. На поверхности такого проводника, тем не менее, может течь ток проводимости и формироваться поверхностный заряд. Поэтому на поверхности идеального проводника

, ,

, .

Силовые линии электрического поля перпендикулярны к поверхности идеального проводника; силовые линии магнитного поля касательны к поверхности идеального проводника, как показано на рис.3.1.3.

Рис.3.1.3. Силовые линии электрического и магнитного полей вблизи поверхности идеального проводника.

Содержание

Граничные условия для векторов напряженности и индукции магнитного поля
Касательная составляющая вектора напряженности магнитного поля
Нормальная составляющая вектора магнитной индукции поля
Готовые работы на аналогичную тему
Касательная составляющая вектора $overrightarrow$ магнитного поля
Закон преломления линий магнитного поля
Граничные условия в магнитном поле
📹 Видео

Видео:Урок 271. Модуль вектора магнитной индукции. Закон АмпераСкачать

Граничные условия для векторов напряженности и индукции магнитного поля

Вы будете перенаправлены на Автор24

При переходе границы между двумя магнетиками с разными магнитными проницаемостями $(mu )$ векторы напряжённости ($overrightarrow$) и индукции ($overrightarrow$) испытывают скачкообразные изменения, которые описываются граничными условиями.

Видео:Лекция №4 "Диэлектрики, вектор электрической индукции"Скачать

Касательная составляющая вектора напряженности магнитного поля

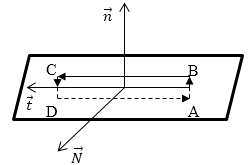
Получим граничное условие для тангенциальной составляющей вектора $overrightarrow$магнитного поля ($H_$). Предположим, что вдоль границы раздела течет поверхностный ток проводимости линейной плотности $overrightarrow$. Построим около границы магнетиков 1 и 2 замкнутый контур (рис. 1).

У этого контура высота пренебрежимо мала по сравнению с длинной основания $l$. Следовательно, вкладом в циркуляцию магнитного поля боковых сторон (AB и СD) пренебрежем. В таком случае имеем:

Правая часть выражения (1) имеет вид:

где $j_n$ —составляющая поверхностной плотности тока вдоль нормали к контуру $overrightarrow=left[overrightarrowoverrightarrowright] $(или, говорят в направлении перпендикулярном тому, в котором выбирают касательные составляющие $overrightarrow$). Надо отметить, что это поверхностные токи проводимости, а не молекулярные токи. Приравняем правые части выражений (2) и (3), получим:

В векторном виде имеем:

В том случае, если тока проводимости на границе раздела нет, то касательные составляющие $overrightarrow$на границе раздела непрерывны:

Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Нормальная составляющая вектора магнитной индукции поля

Граничное условие для $B_n$получают из уравнения:

Перпендикулярные составляющие $overrightarrow$на границе раздела двух магнетиков непрерывны:

Готовые работы на аналогичную тему

Нормальная составляющая вектора $overrightarrow$Из уравнения (8), если применить материальное уравнение для векторов магнитного поля при переходе из одной среды в другую имеем:

Видео:Линии магнитной индукции наглядно. Правило правой рукиСкачать

Касательная составляющая вектора $overrightarrow$ магнитного поля

Тангенциальные составляющие магнитного поля испытываю скачек, причем:

Выражения (4, 6), (8), (9), (10) являются граничными условиями для магнитного поля. Они аналогичны граничным условиям для электрического поля.

Видео:1.1 Векторы напряженности и индукции электрического и магнитного полейСкачать

Закон преломления линий магнитного поля

Из граничных условий для магнитного поля следует закон преломления линий индукции:

где $_1$ — угол между линиями магнитной индукции в среде 1 и нормалью к поверхности раздела, $_2$- гол в среде 2. Так как в изотропных средах направления вектора $overrightarrow$ и вектора $overrightarrow$ совпадают, то закон (11) является и законом преломления линий напряженности. Из (11) следует, что если линии поля переходят из среды с меньшей магнитной проницаемостью в среду с большей проницаемостью, то они удаляются от нормали, и линии сгущаются.

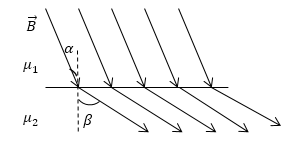
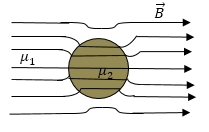
Задание: На рис. 2 изображены линий вектора $overrightarrow $при переходе их одного магнетика ($_1$) в другой ($_2$). Какая из магнитных проницаемостей среды больше?

Рассмотрим, поведение силовых линий, когда они переходят границу двух магнетиков. Если отсутствуют поверхностные токи, выполняется условие:

Это означает, что в магнетике с большей магнитной проницаемостью, вектор $overrightarrow$ составляет больший угол с нормалью к границе раздела двух магнетиков.

Следовательно, в нашей задаче $_2 > _1$.

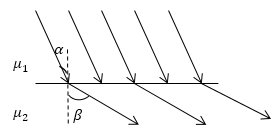
Задание: Магнитное поле на границе двух магнетиков изобразили с помощью линий поля (рис.3). Какие это линии, какая из магнитных проницаемостей среды больше?

На рис.3 изображены линии напряженности магнитного поля ($overrightarrow$), так как мы знаем, что они на границе магнетиков испытывают разрыв. Это является следствием связанных токов на границе раздела. Тогда как линии индукции магнитного поля не прерываются.
$_2 >_1,$ так как в среде с большей магнитной проницаемостью линии поля имею больший угол между нормалью к границе раздела сред согласно закону преломления.

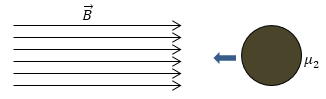
Задание: В однородное поле помещают шар из магнетика, изобразите линии индукции магнитного поля. Считайте, что магнитная проницаемость шара больше, чем проницаемость окружающей среды.

В ситуации, которая задана линии индукции в теле шаровой формы будут параллельными линиями, значение индукции во всех точках шара одинаковое. При этом будут постоянны напряженность и намагниченность, то есть, говорят, что шар намагничен однородно. Кроме того рис. 5 учитывает, что $_2 > _1.$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 11 02 2022

Видео:ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ сила Ампера правило левой рукиСкачать

Граничные условия в магнитном поле

Напряженность магнитного поля на границе раздела сред.

Магнитные линии на границе раздела двух сред с различными магнитными проницаемостями претерпевают преломление. Выведем закон этого преломления, получив предварительно весьма важные для практики условия для напряженности МП и магнитной индукции на границе двух сред. При этом ограничимся рассмотрением частного случая равномерного поля в двух однородных средах с магнитными проницаемостями JLlj и JLX2, граничащими по плоской поверхности (рис. 3.5), обозначив углы, составляемые магнитными линиями в одной и второй средах с плоскостью раздела сред [3.5] соответственно через и 02 •

Рис. 3.5. Распределение напряженности однородного МП у плоской границы раздела сред

Рассмотрим замкнутый контур в виде весьма узкого прямоугольника ABCD (рис. 3.5), расположенного у границы раздела сред так, чтобы его длинные стороны АВ и CD оказались в двух разных средах и параллельными плоскости раздела между средами. Применим для этого контура закон полного тока:

предполагая, что на границе раздела двух сред никаких токов не протекает, т. е. считая ток / , сцепляющийся с контуром интегрирования, равным нулю,

Разбивая интеграл по замкнутому контуру (3.28) на четыре интеграла по четырем прямым участкам пути интегрирования и пренебрегая интегралами по весьма коротким участкам ВС и DA по сравнению с интегралами по длинным участкам АВ и CD, будем иметь

где Н и Н2 — напряженности МП соответственно в первой и второй средах, а 0Ц и (Х^- углы, составляемые векторами Н и Н2 с элементами dl пути интегрирования по первому и второму участникам (обход контура при интегрировании предполагаем по часовой стрелке).

Поскольку поля в обеих средах равномерны, векторы напряженности при переходе от точки к точке по пути интегрирования в пределах одной среды остаются неизменными как по величине, так и по направлению. Принимая также во внимание прямолинейность путей интегрирования и, следовательно, постоянство углов СХj и СС2 ? можно

величины Н и Н2, COS ОС> и COS 012 вынести из-под интегралов.

Так как оставшиеся интегралы от элементов dl пути интегрирования будут представлять собой длины этих участков, то предыдущее равенство можно записать в виде

Сокращая равенство на равные друг другу отрезки I и /₍

выражая углы ОЦ и ОС 2 через исходные углы 0j и 02 ( OCj = 0,5л — 0j, ОС2 — 0,5л + 02 ), получим

т.е. на границе раздела двух сред равны касательные составляющие вектора напряженности магнитного поля.

Магнитная индукция на границе раздела сред. Представим теперь на границе раздела двух сред весьма тонкий параллелепипед (рис. 3.6), две большие грани 5] и ^ которого, параллельные плоскости

раздела, расположены соответственно в первой и второй средах. Запишем для замкнутой поверхности этого параллелепипеда принцип непрерывности магнитных линий:

Разбивая интеграл по замкнутой поверхности на три интеграла (по плоскостям S ,^2 И боковой поверхности параллелепипеда Sq ) и

пренебрегая ввиду малости поверхности S q последним интегралом по сравнению с двумя предыдущими, будем иметь

т. е. на границе раздела двух сред равны нормальные составляющие векторов магнитной индукции.

Рис. 3.6. Распределение индукции однородного МП у плоской границы раздела сред

Закон преломления. Из полученных выше выводов относительно равенства касательных составляющих векторов напряженности МП:

и нормальных составляющих векторов магнитной индукции:

разделив первое равенство на второе, нетрудно получить закон преломления магнитных линий

или, принимая во внимание, что В / Н = Л ,

Таким образом, отношение тангенсов углов падения и преломления магнитных линий при переходе через границу раздела двух сред равно отношению магнитных проницаемостей этих сред.

Направление магнитного поля у поверхности ферромагнитных тел. Остановимся на примере, иллюстрирующем применение последнего закона и раскрывающем весьма важное положение о направлении МП вблизи тел из ферромагнитного материала, в частности вблизи стальных магнитопроводов различных электромагнитных устройств.

В связи с тем, что магнитная проницаемость ферромагнитного вещества во много раз больше магнитной проницаемости материала, обычно окружающего магнитопровод (воздух, масло, пластмасса и т.

д.), различие в тангенсах углов 0j и 02, составляемых магнитными

линиями и нормалью к плоскости раздела сред должно быть также весьма большим. Если, например, в ферромагнитной среде с магнитной

проницаемостью J4 = 100 JLX q магнитная линия будет подходить к

границе раздела почти по касательной (на рис. 4.3 0j =85^), то в воздух эта магнитная линия выйдет почти перпендикулярно поверхности раздела (02 = 5 ). В подавляющем большинстве практических

случаев, когда мы имеем дело с магнитопроводами, выполненными из стали, магнитная проницаемость которой в несколько тысяч раз превышает магнитную проницаемость воздуха, угол 02 выхода магнитных линий из магнитопроводов еще значительно меньше. Поэтому принято считать, что магнитные линии выходят из стальных тел или входят в них практически под прямым углом к их поверхности.

Рассмотрим границу между ферромагнитным материалом и воздухом ()1Ц » JU-2)- В этом случае tgOCj » tgCX 2 ; линия магнитной индукции, подходящая к границе под острым углом в стали, будет выходить в воздухе под углом ОС 2, тангенс которого мал. Практически

можно считать угол ОС 2 близким к нулю; другими словами, линии магнитной индукции выходят из стали в воздух практически по нормали к поверхности стали. Это правило, однако, нельзя распространять на современные материалы для постоянных магнитов, магнитная проницаемость которых мала. Правило действительно лишь в случаях, когда провода с токами, определяющими МП, расположены в воздухе, а не в стали.