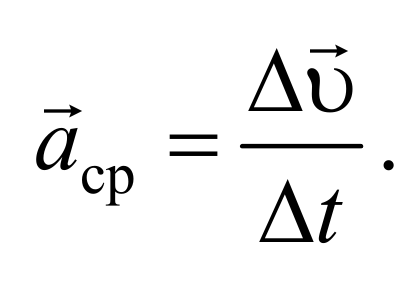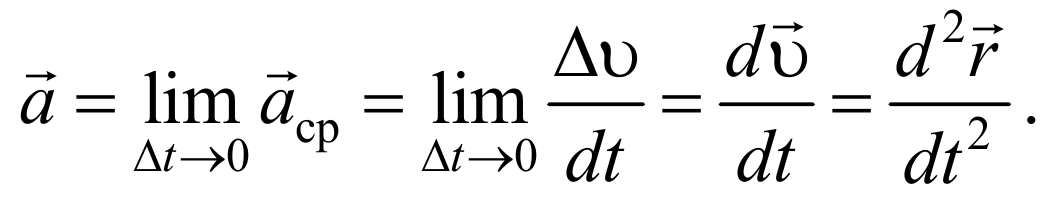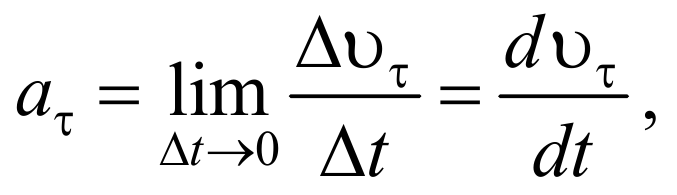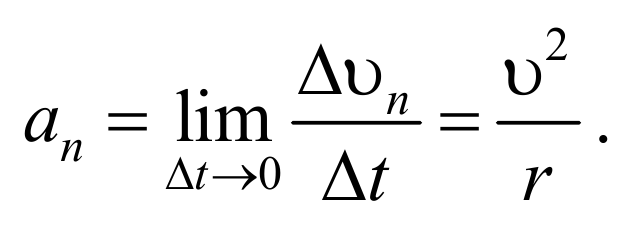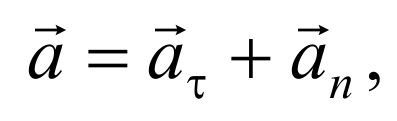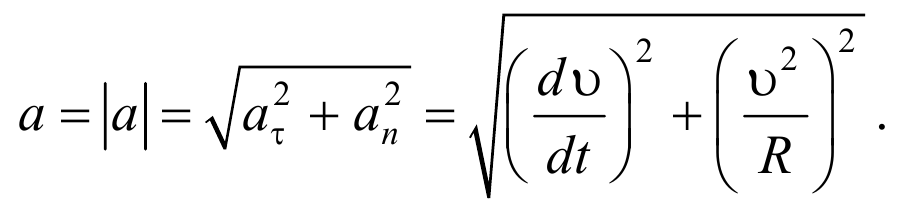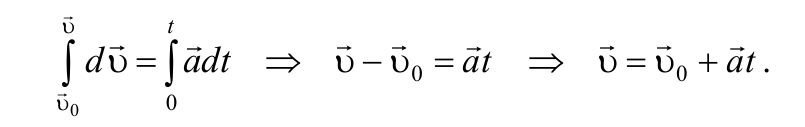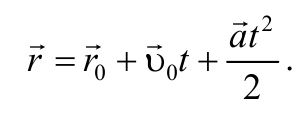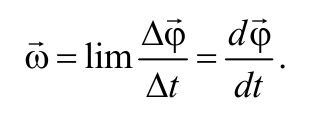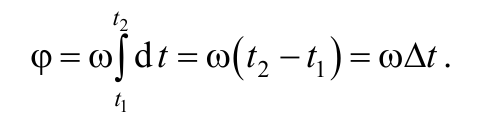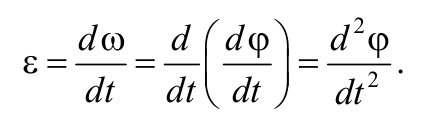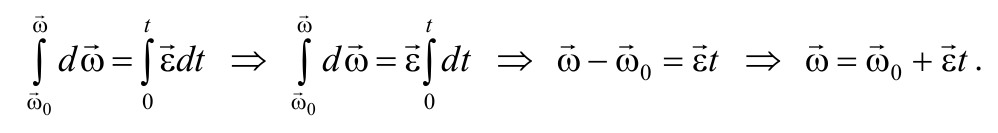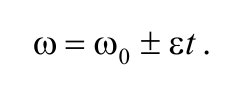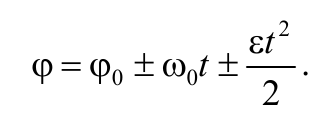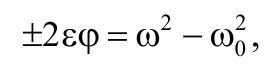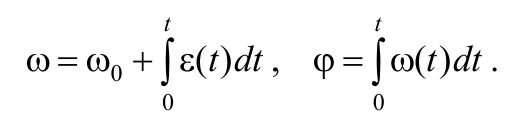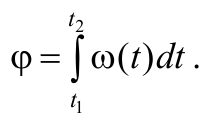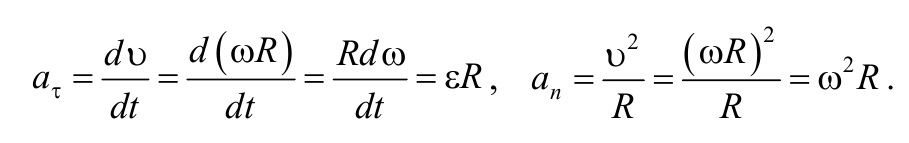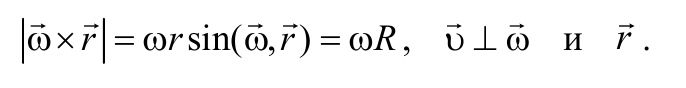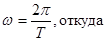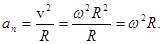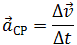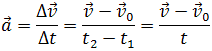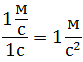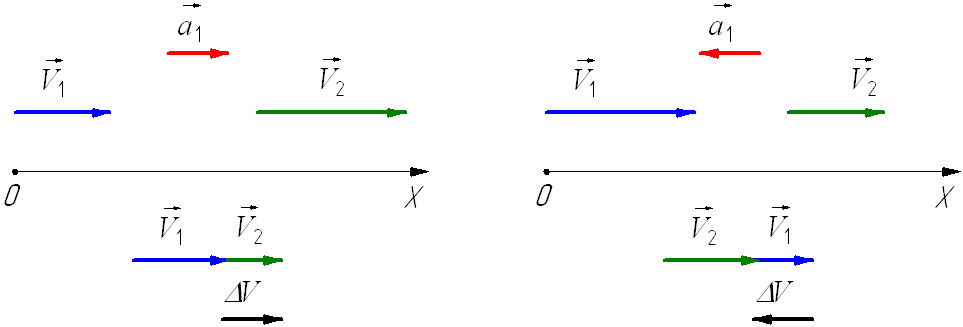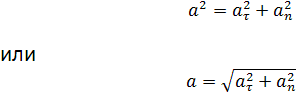- Лекция №2. Элементы кинематики
- 1.4. Нормальное и тангенциальное ускорения при криволинейном движении
- 1.5. Классификация движений материальной точки
- 1.6. Кинематика абсолютно твердого тела
- 1.7. Связь между линейными и угловыми характеристиками тела при его вращении
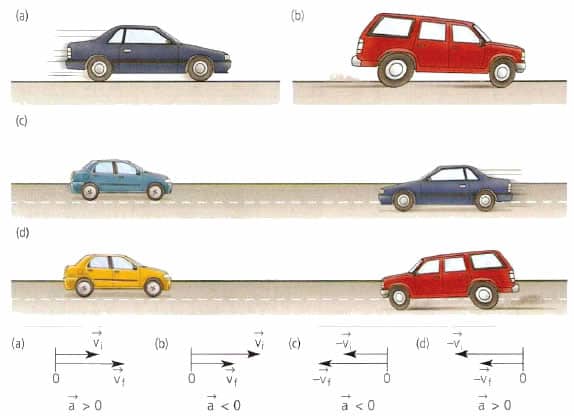
- Векторы ускорения и скорости. Ускорение и сила. Направления тангенциального и нормального ускорений
- Что такое скорость и ускорение?
- Куда направлены векторы ускорения и скорости?
- Действующая на тело сила и ускорение
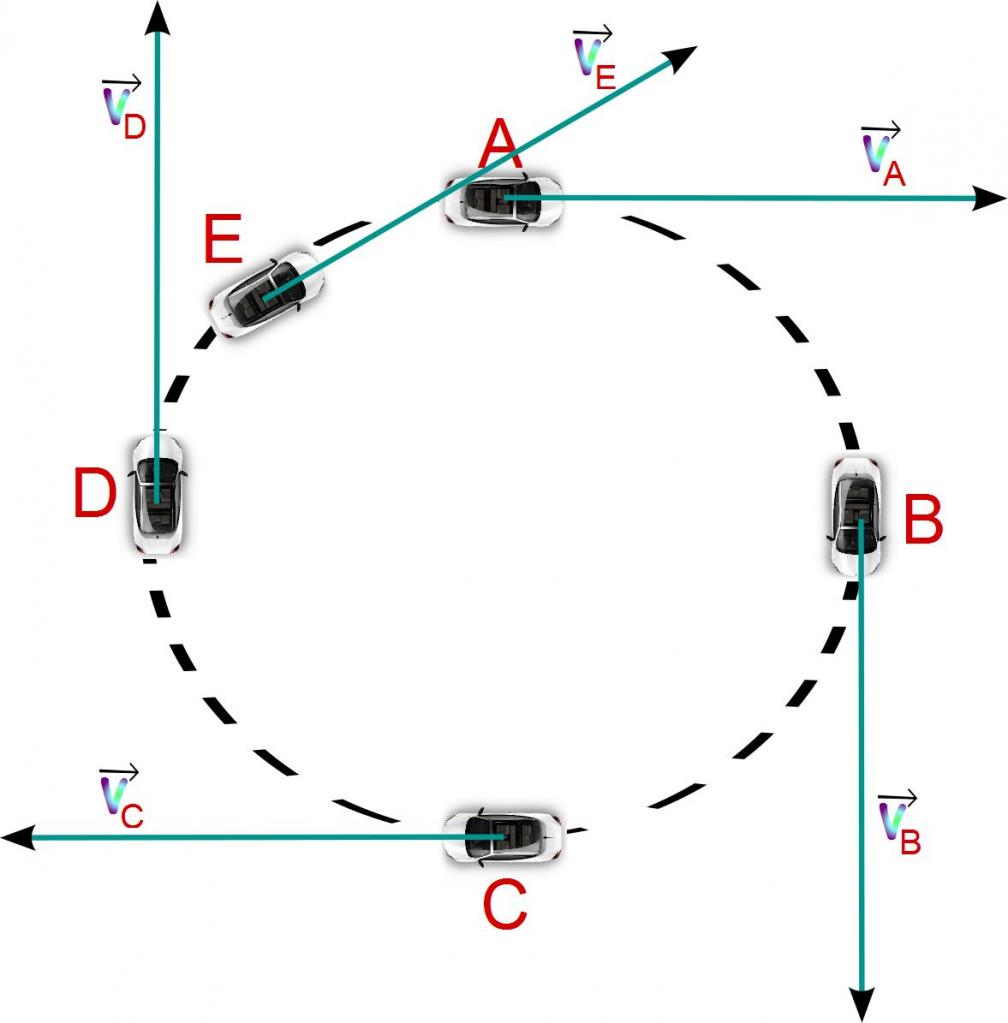
- Движение по окружности и ускорение
- Тангенциальное ускорение определяется по формуле
- В физике
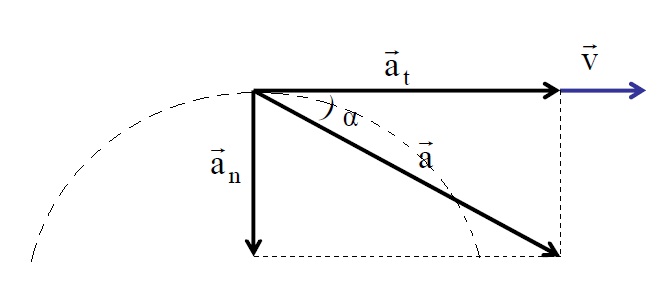
- Траектория движения и компоненты полного ускорения
- Ускорение тангенциальное
- Ускорение нормальное
- Ускорение полное, нормальное и тангенциальное
- Решение задачи
- Ускорение
- Среднее ускорение
- Мгновенное ускорение
- Тангенциальное ускорение
- Нормальное ускорение
- Полное ускорение
- физ. Физика.Ответы.Теория. Кинематика материальной точки. Радиусвектор, скорость и ускорение. Нормальная и тангенциальная составляющие ускорения. Радиус кривизны траектории.
Видео:Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать

Лекция №2. Элементы кинематики
1.4. Нормальное и тангенциальное ускорения при криволинейном движении
В общем случае при движении тела его скорость изменяется как по величине, так и по направлению. Для характеристики быстроты изменения скорости движения вводится понятие ускорения.
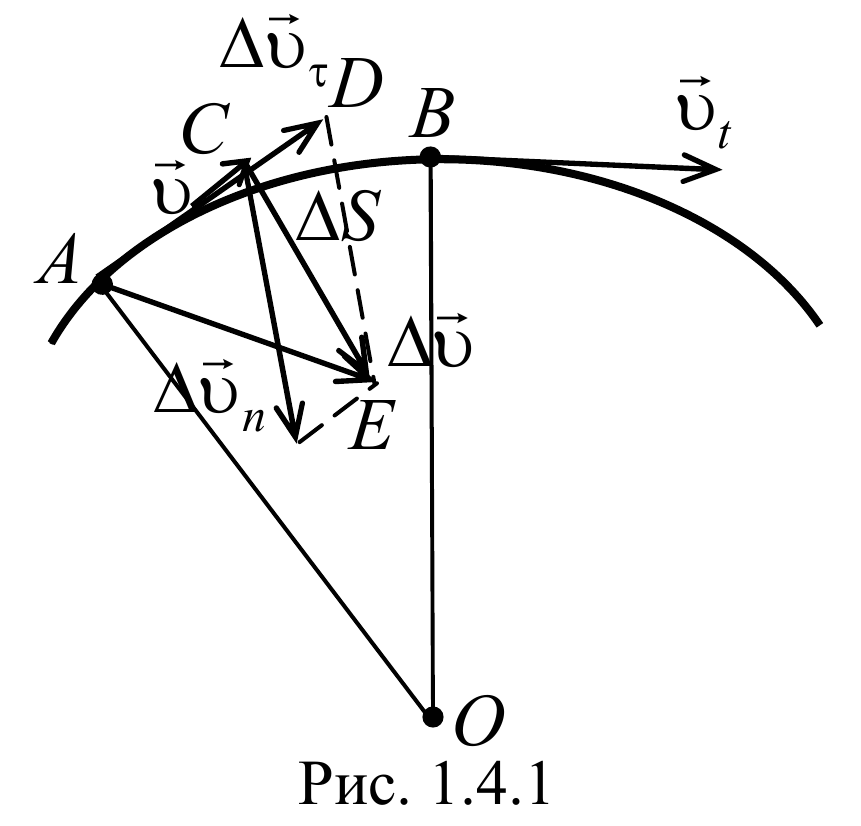
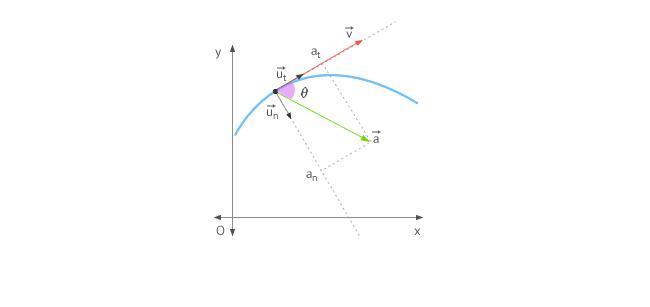
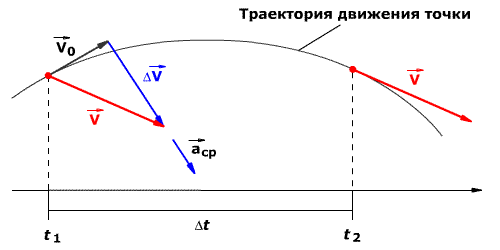
Рассмотрим плоское движение, т. е. такое, при котором все участки траектории точки лежат в одной плоскости. Пусть вектор υ задает скорость точки А , в момент времени t . За время Δt движущаяся точка перешла в положение В и приобрела скорость, отличную от υ как по модулю, так и направлению и равную υ1 = υ +Δ υ . Перенесем вектор υ1 в точку А и найдем Δ υ (рис.). Средним ускорением aср неравномерного движения в интервале времени от t до t+Δt называется векторная величина, равная отношению изменения скорости Δ υ к интервалу времени Δt :
Ускорение в данный момент времени (мгновенное ускорение) представляет собой предел, к которому стремится выражение (1.4.1) при Δt 0 , т. е.
Таким образом, ускорение есть векторная величина, равная первой производной скорости по времени.
Разложим вектор Δ υ на две составляющие. Для этого из точки А (рис. 1.4.1) по направлению скорости υ отложим вектор AD , по модулю равный υ1 . Очевидно, что вектор CD , равный Δ υτ , определяет изменение скорости по модулю за время Δt : Δυτ=υ1−υ . Вторая же составляющая Δυn вектора Δ υ характеризует изменение скорости за время Δt no направлению.
Тангенциальная составляющая ускорения
т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.
Определим вторую составляющую ускорения. Допустим, что точка B близка к точке A , поэтому Δs можно считать дугой окружности некоторого радиуса r , мало отличающейся от хорды AB . Тогда из подобия треугольников AOB и EAD следует Δυn/AB=υ1/r , но так как AB=υΔt , то Δυn/t=υυ1/r . В пределе Δt 0 , получим υ1 υ .
Поскольку υ1 υ , угол EAD стремится к нулю, а так как треугольник EAD равнобедренный, то угол АDE между υ и Δ υn стремится к прямому. Следовательно, при Δt 0 векторы υ и Δ υn оказываются взаимно перпендикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор Δ υn , перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны. Поэтому эту составляющую ускорения называют также центростремительным ускорением.
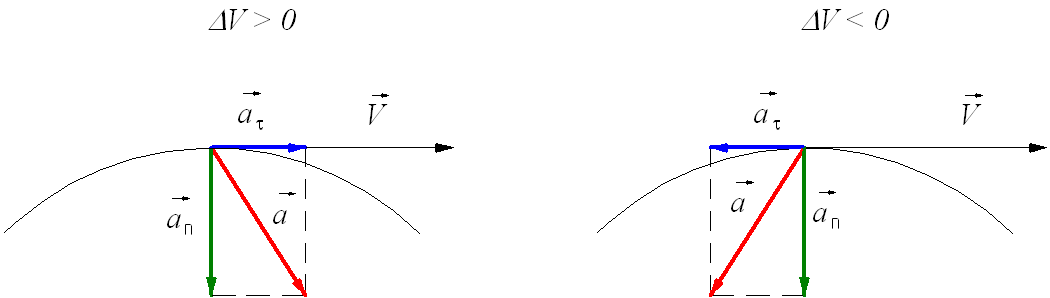
Таким образом, полное ускорение тела a есть геометрическая сумма тангенциальной aτ и нормальной an составляющих
Тангенциальное ускорение равно первой производной по времени от модуля скорости и определяет быстроту изменения скорости по модулю, и направлено по касательной к траектории.
Нормальное ускорение определяет быстроту изменения скорости по направлению и направлено к центру кривизны траектории.
Векторы aτ и an взаимно перпендикулярны поэтому модуль полного ускорения равен
1.5. Классификация движений материальной точки
В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:
1) aτ=0,an=0 — прямолинейное равномерное движение.
2) aτ=const,an=0 — прямолинейное равнопеременное движение.
Так как $$vec = over dt>$$ , то, проинтегрировав полученное выражение в пределах от нуля до произвольного момента времени можно найти перемещение точки: 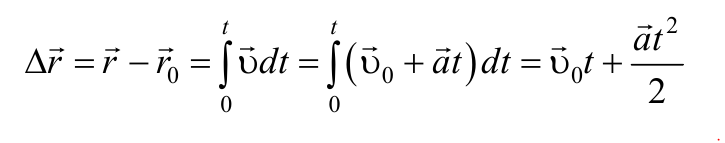
3) aτ= ƒ(t), an=0 − прямолинейное движение с переменным ускорением.
4) aτ=0, an=const — При таком движении скорость точки не изменяется по модулю, так как тангенциальная составляющая равна нулю, а изменяется только по направлению.
5) aτ=const, an≠const − равнопеременное движение по окружности.
6) aτ=0, an≠0 − равномерное криволинейное движение.
7) aτ=const, an≠0 − криволинейное равнопеременное движение.
1.6. Кинематика абсолютно твердого тела
Вращательное движение − это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. При вращательном движении скорости и ускорения различных точек тела неодинаковы. Поэтому в качестве общих кинематических характеристик движения тела при вращении вводятся угол поворота, угловая скорость и угловое ускорение тела. При вращении тела угол поворота изменяется со временем по некоторому закону ϕ = ϕ(t) , который называется уравнением вращательного движения тела.
Угловой скоростью тела называется вектор, численно равный первой производной по времени от угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:
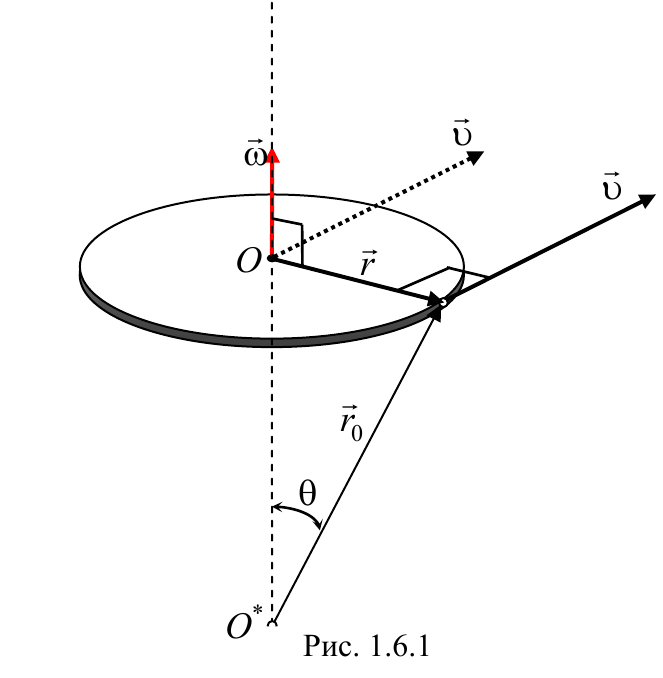
Вектор угловой скорости направлен по оси вращения, причем так, чтобы вращение, рассматриваемое с конца вектора угловой скорости, происходило против хода часовой стрелки (рис 1.6.1). Единицей угловой скорости является рад/с.
Скорость произвольной точки вращающегося тела называется линейной скоростью этой точки.
При равномерном вращении угловая скорость не изменяется со временем, то есть является постоянной величиной (ω = const) . Тогда
Равномерное вращение характеризуется периодом вращения и частотой вращения.
Период вращения − это время, за которое точка совершает один полный оборот, т. е. поворачивается на угол ϕ = 2π и на основании выражения (1.6.1) $$ = over ω>$$
Частота вращения − это число полных оборотов, которое делает точка при равномерном вращении, за единицу времени: $$ = = $$ , откуда ϕ = 2πn .
Для характеристики неравномерного вращения тела вводится понятие углового ускорения .
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
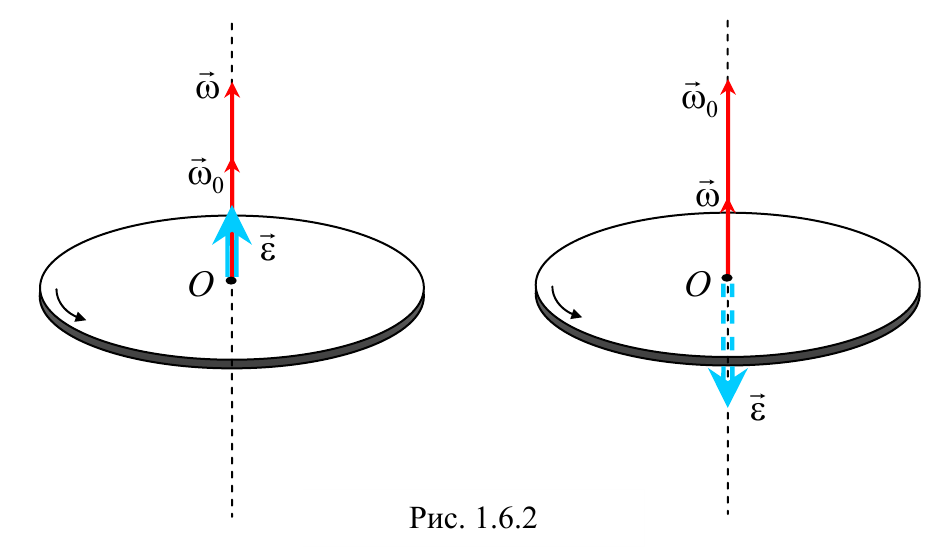
При ускоренном вращении вектор углового ускорения сонаправлен с вектором угловой скорости, а при замедленном − противоположен ему.
В случае равнопеременного движения точки по окружности (ε = const) угловая скорость определяется по формуле
Или в скалярном виде
Проинтегрировав выражение (1.6.1) можно получить формулу для угла поворота тела
Исключив из последнего уравнения t , получим
где φ = 2πN , N − число полное число оборотов, совершенных телом.
В случае ε = ε(t) , угловая скорость и закон вращательного движения определяются следующими формулами
1.7. Связь между линейными и угловыми характеристиками тела при его вращении
За время dt точка проходит по дуге окружности радиуса R путь dS = Rdφ . Поэтому $$ = = = $$ .
Если угол поворота вращающегося тела представить в виде dφ = ω(t)dt и проинтегрировать в пределах от начального момента времени t1 до конечного момента времени t2 , то получится угол, на который совершила поворот тело за время:
Тангенциальная и нормальная составляющие ускорения произвольной точки тела, вращающегося вокруг неподвижной оси, определяются формулами:
Полученные соотношения (1.7.1) можно записать в векторном виде. Для этого на оси вращения ОО* (рис. 1.6.1) тела выберем любую точку A и проведем из нее радиус-вектор r в точку M . Векторное произведение ω × r по модулю и направлению совпадает с вектором скорости υ точки M :
Следовательно, можно записать, что вектор скорости υ = ω × r , а вектор ускорения точки
Видео:Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Векторы ускорения и скорости. Ускорение и сила. Направления тангенциального и нормального ускорений
Как известно, любая физическая величина относится к одному из двух типов, она является либо скалярной, либо векторной. В данной статье рассмотрим такие кинематические характеристики как скорость и ускорение, а также покажем, куда направлены векторы ускорения и скорости.
Видео:Рассмотрение темы: "Тангенциальное, нормальное и полное ускорение"Скачать
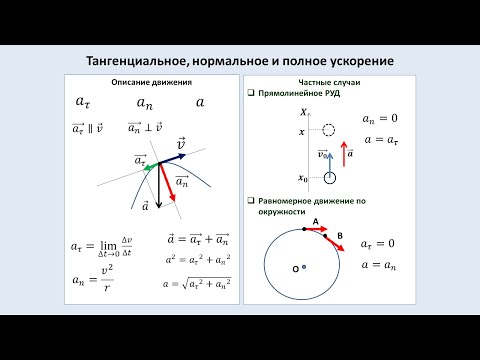
Что такое скорость и ускорение?
Обе величины, названные в этом пункте, являются важными характеристиками любого вида движения, будь то перемещение тела по прямой линии или по криволинейной траектории.

Скоростью называется быстрота изменения координат во времени. Математически эта величина равна производной по времени пройденного пути, то есть:
Здесь вектор l¯ направлен от начальной точки пути к конечной.
В свою очередь ускорение – это скорость, с которой изменяется во времени сама скорость. В виде формулы оно может быть записано так:
Очевидно, что взяв вторую производную от вектора перемещения l¯ по времени, мы также получим значение ускорения.
Поскольку скорость измеряется в метрах в секунду, то ускорение, согласно записанному выражению, измеряется в метрах в секунду в квадрате.
Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Куда направлены векторы ускорения и скорости?
В физике всякое механическое движение тела принято характеризовать определенной траекторией. Последняя представляет собой некоторую воображаемую кривую, вдоль которой тело перемещается в пространстве. Например, прямая линия или окружность — это яркие примеры распространенных траекторий движения.
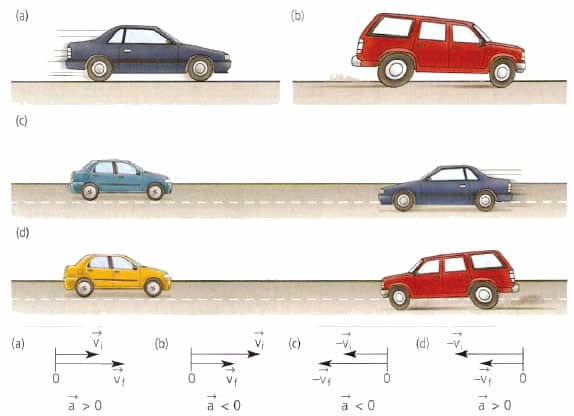
Вектор скорости тела направлен в сторону движения всегда, независимо от того, замедляется или ускоряется тело, движется оно по прямой или по кривой. Если говорить геометрическими терминами, то вектор скорости направлен по касательной к точке траектории, в которой в данный момент находится тело.
Вектор ускорения точки материальной или тела не имеет ничего общего со скоростью. Этот вектор направлен в сторону изменения скорости. Например, для прямолинейного движения величина a¯ может как совпадать по направлению с v¯, так и быть противоположной v¯.
Видео:Физика - Магнитное полеСкачать

Действующая на тело сила и ускорение
Мы выяснили, что вектор ускорения тела направлен в сторону изменения вектора скорости. Тем не менее не всегда можно легко определить, как меняется скорость в данной точке траектории. Более того, для определения изменения скорости необходимо выполнить операцию разности векторов. Чтобы избежать этих трудностей в определении направления вектора a¯, существует еще один способ быстро его узнать.
Ниже записан знаменитый и хорошо известный каждому школьнику закон Ньютона:
Формула показывает, что причиной возникновения ускорения у тел является действующая на них сила. Поскольку масса m является скаляром, то вектор силы F¯ и вектор ускорения a¯ направлены одинаково. Этот факт следует запомнить и применять на практике всегда, когда возникает необходимость в определении направления величины a¯.
Если на тело действуют несколько разных сил, тогда направление вектора ускорения будет равно результирующему вектору всех сил.
Видео:Составляющие вектораСкачать

Движение по окружности и ускорение
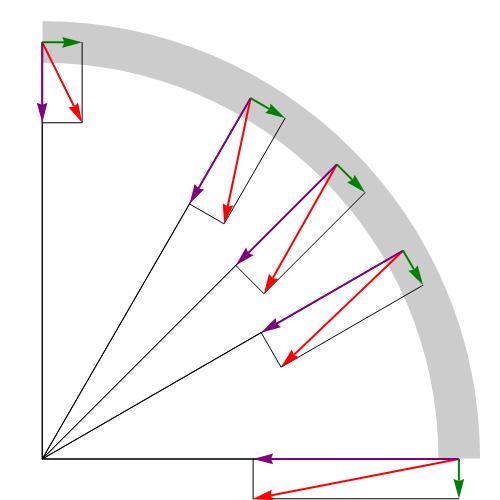
Когда тело перемещается по прямой линии, то ускорение направлено либо вперед, либо назад. В случае же движения по окружности ситуация усложняется тем, что вектор скорости постоянно меняет свое направление. В виду сказанного, полное ускорение определяется двумя его составляющими: тангенциальным и нормальным ускорениями.
Тангенциальное ускорение направлено точно так же, как вектор скорости, или против него. Иными словами, эта компонента ускорения направлена вдоль касательной к траектории. Ускорение тангенциальное описывает изменение модуля самой скорости.
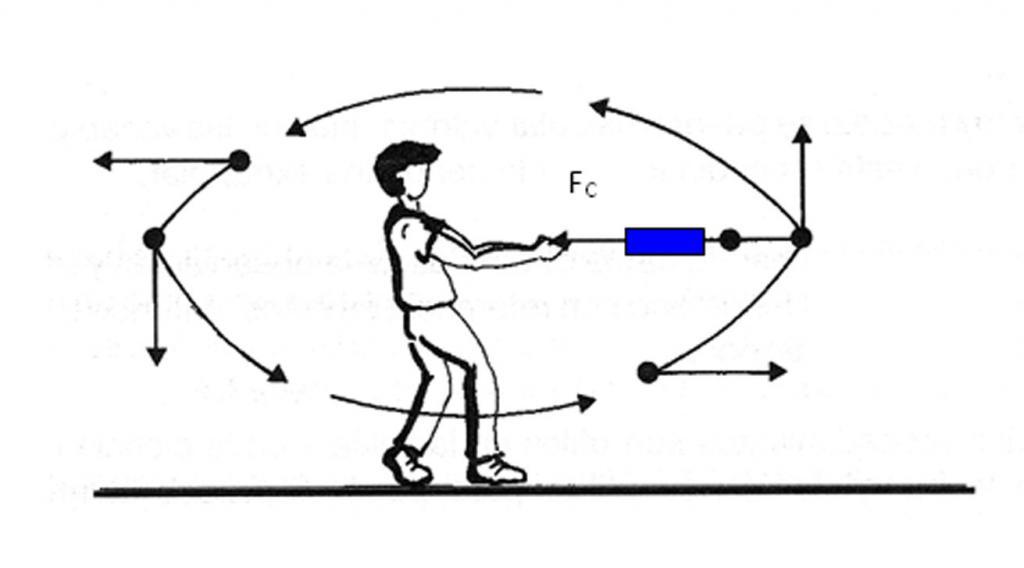
Ускорение нормальное направлено вдоль нормали к данной точке траектории с учетом ее кривизны. В случае движения по окружности вектор этой компоненты указывает на центр, то есть нормальное ускорение направлено вдоль радиуса вращения. Эту компоненту часто называют центростремительной.
Полное ускорение представляет собой сумму названных компонент, поэтому его вектор может быть направлен произвольным образом по отношению к линии окружности.
Если тело совершает вращение без изменения линейной скорости, то существует отличная от нуля только нормальная компонента, поэтому вектор полного ускорения направлен к центру окружности. Заметим, что к этому центру также действует сила, удерживающая тело на его траектории. Например, сила гравитации Солнца удерживает нашу Землю и другие планеты на своих орбитах.
Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Тангенциальное ускорение определяется по формуле
Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения.
Если тело движется по криволинейной траектории, то его скорость направлена по касательной к этой траектории.
Так как направление скорости все время меняется, значит, в таком случае криволинейное движение всегда происходит с ускорением, также, если модуль скорости не меняется.
В большинстве случаев ускорение направлено под некоторым углом к скорости. Составляющую ускорения, которая направлена вдоль скорости, называют тангенциальным ускорением 
Нормальное ускорение 
Здесь R – это радиус кривизны траектории в заданной точке.
Тангенциальное и нормальное ускорение всегда имеют перпендикулярное направление, откуда получаем модуль полного ускорения:

Нормальное, тангенциальное и полное ускорение
Ускорение при криволинейном движении
В случае движения материальной точки по криволинейной траектории различают нормальное и тангенциальное ускорения.
Нормальное (центростремительное) ускорение 
Модуль нормального ускорения определяют по формуле 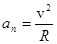
Тангенциальное (касательное) ускорение 
Модуль тангенциального ускорения определяют по формуле 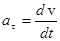
Модуль полного ускорения 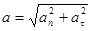
Тело, деформациями которого в данных условиях движения, можно пренебречь называют абсолютно твердым телом.
При вращательном движении радиус-вектор каждой точки поворачивается за одно и то время 
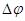
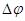
Угловой скоростью тела называют величину
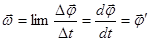
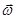
Равномерное вращение характеризуется периодом обращения Т.
Периодом обращения называют промежуток времени, за которое тело делает один полный оборот (поворачивается на угол 2π).
Модуль угловой скорости равномерного движения

Частотой обращения называют число оборотов точки за единицу времени 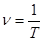
Таким образом,
Угловое ускорение характеризует быстроту изменения угловой скорости (в случае неравномерного вращения)

Линейная скорость тела связана с угловой соотношением 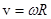
Модуль нормального ускорения
Модуль тангенциального ускорения 
Дата добавления: 2014-11-18 ; Просмотров: 889 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
В кинематике для однозначного определения характеристик движения тела в любой точке траектории необходимо знать его скорость и ускорение. Зависимость от времени этих величин предоставляет всю необходимую информацию для вычисления пройденного телом пути. Рассмотрим подробнее в статье, что такое ускорение тангенциальное и нормальное ускорение.
Видео:46. Граничные условия для электрического поляСкачать

В физике
Прежде чем рассматривать для механического движения ускорение нормальное и тангенциальное ускорение, познакомимся с самим физическим понятием. Определение ускорения является достаточно простым. В физике под ним понимают характеристику изменения скорости. Последняя является векторной величиной, определяющей быстроту изменения координат движущегося объекта в пространстве. Скорость измеряется в метрах в секунду (расстояние, пройденное за единицу времени). Если ее обозначить символом v¯, тогда математическое определение ускорения a¯ будет выглядеть так:
Это равенство определяет так называемое полное мгновенное ускорение. Мгновенным оно называется потому, что характеризует изменение скорости лишь в данный момент времени.
Если движение является равноускоренным, то есть в течение длительного времени ускорение не меняет своего модуля и направления, тогда можно записать следующую формулу для его определения:
Где Δt>>dt. Величина a¯ здесь называется средним ускорением, которое в общем случае отличается от мгновенного.
Ускорение измеряется в системе СИ в метрах в квадратную секунду (м/с 2 ).
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Траектория движения и компоненты полного ускорения
Чаще всего тела в природе движутся по кривым траекториям. Примерами такого перемещения являются: вращение по своим орбитам планет, параболическое падение камня на землю, поворот автомобиля. В случае криволинейной траектории в любой момент времени скорость направлена по касательной к рассматриваемой точке траектории. Как при этом направлено ускорение?
Чтобы ответить на поставленный выше вопрос, запишем скорость тела в следующей форме:
Здесь ut¯ – вектор скорости единичный, индекс t означает, что он направлен по касательной к траектории (тангенциальная компонента). Символом v обозначен модуль скорости v¯.
Теперь, следуя определению ускорения, можно провести дифференцирование скорости по времени, имеем:
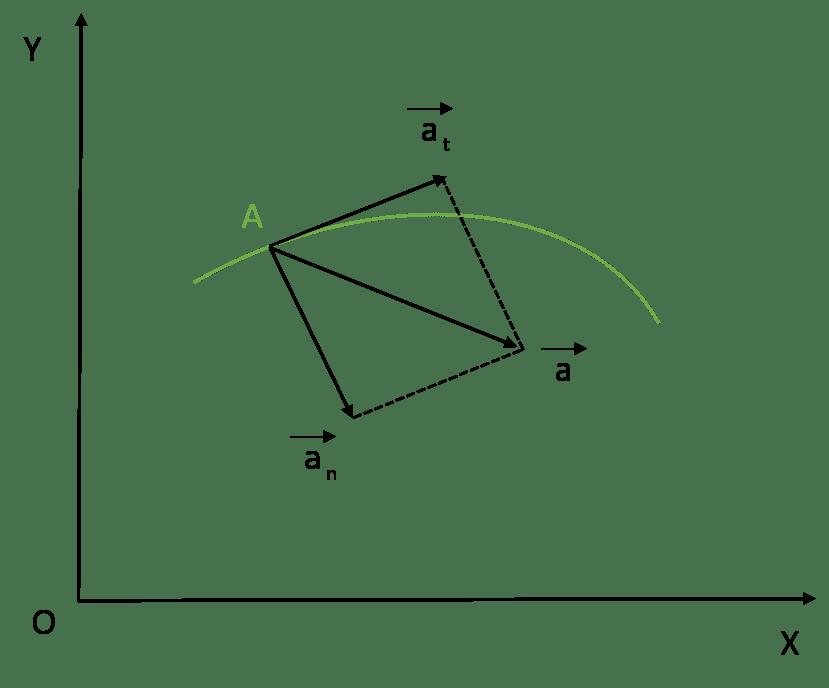
Таким образом, полное ускорение a¯ представляет собой векторную сумму двух компонент. Первое и второе слагаемое называются нормальным и тангенциальным ускорением точки. Подробнее рассмотрим каждую из этих компонент.
Видео:Лекция 4-2. Условия на границе раздела двух диэлектриковСкачать

Ускорение тангенциальное
Запишем еще раз формулу для этой компоненты полного ускорения:
Это выражение позволяет описать свойства величины at¯:
- Она направлена точно так же, как и сама скорость или противоположно ей, то есть по касательной к траектории. Об этом свидетельствует элементарный вектор ut¯.
- Она характеризует изменение скорости по абсолютной величине, что отражает множитель dv/dt.
Эти свойства позволяют сделать важный вывод: для прямолинейного движения полное и тангенциальное ускорения – это одна и та же величина. В случае криволинейного перемещения полное ускорение всегда больше по модулю, чем тангенциальное. Когда рассматривают физические задачи на прямолинейное равноускоренное движение, то ведут речь именно об этой компоненте ускорения.
Видео:Разложение вектора по базису. 9 класс.Скачать

Ускорение нормальное
Рассматривая тему скорости, ускорения тангенциального и ускорения нормального, дадим характеристику последней величине. Запишем формулу для нее:
Чтобы записать явно правую часть равенства, воспользуемся следующими соотношениями:
Здесь dL – это пройденный телом путь за промежуток времени dt, r – радиус кривизны траектории. Первое выражение соответствует определению скорости, второе равенство следует из геометрических соображений. Пользуясь этими формулами, получаем конечное выражение для нормального ускорения:
То есть величина an¯ не зависит от изменения скорости, как тангенциальная компонента, а определяется исключительно ее модулем. Нормальное ускорение вдоль нормали к данному участку траектории направлено, то есть к центру кривизны. Например, во время движения по окружности вектор an¯ направлен к ее центру, поэтому нормальное ускорение называют часто центростремительным.
Если за изменение абсолютной величины скорости ответственно ускорение тангенциальное, то нормальная компонента ответственна за изменение вектора скорости, то есть она определяет траекторию перемещения тела.
Видео:2.5 Граничные условия для векторов поля на поверхности раздела средСкачать
Ускорение полное, нормальное и тангенциальное
Разобравшись с понятием ускорения и с его компонентами, приведем теперь формулу, которая позволяет определить полное ускорение. Поскольку рассмотренные компоненты направлены под углом 90 o друг к другу, то для определения абсолютной величины их векторной суммы можно использовать теорему Пифагора. Формула для полного ускорения имеет вид:
Направление величины a¯ можно определить по отношению к вектору любой из компонент. Например, угол между a¯ и an¯ вычисляется так:
Учитывая приведенную выше формулу для модуля a¯, можно сделать вывод: при равномерном движении по окружности полное ускорение совпадает с центростремительным.
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Решение задачи
Пусть тело движется по окружности радиусом 1 метр. Известно, что его скорость изменяется по следующему закону:
Необходимо определить ускорение тангенциальное и нормальное ускорение в момент t = 4 секунды.
Для тангенциального имеем:
Для того чтобы найти модуль ускорения нормального, сначала следует вычислить значение скорости в заданный момент времени. Имеем:
Теперь можно воспользоваться формулой для an:
Таким образом, мы определили все величины, которые требовалось найти для решения задачи.
Видео:Кинематика материальной точки. Тангенциальное и нормальное ускорение. Классическая механика Лекция 1Скачать

Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Видео:Центростремительное ускорение. 9 класс.Скачать

Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
где 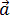
Направление вектора ускорения совпадает с направлением изменения скорости Δ 



В момент времени t1 (см. рис 1.8) тело имеет скорость 




Рис. 1.8. Среднее ускорение.
В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с 2 , то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
Видео:Вращательное движение. 10 класс.Скачать

Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
Направление ускорения также совпадает с направлением изменения скорости Δ 
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть а направление вектора ускорения совпадает с вектором скорости 
Если скорость тела по модулю уменьшается, то есть то направление вектора ускорения противоположно направлению вектора скорости 
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Видео:Единичные векторы и инженерная запись (видео 34) | Криволинейное движение | ФизикаСкачать

Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения 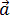
Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 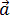
Видео:Преломление силовых линий напряженности (отв.22)Скачать

Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

физ. Физика.Ответы.Теория. Кинематика материальной точки. Радиусвектор, скорость и ускорение. Нормальная и тангенциальная составляющие ускорения. Радиус кривизны траектории.
| Название | Кинематика материальной точки. Радиусвектор, скорость и ускорение. Нормальная и тангенциальная составляющие ускорения. Радиус кривизны траектории. |
| Дата | 19.01.2020 |
| Размер | 5.2 Mb. |
| Формат файла |  |
| Имя файла | Физика.Ответы.Теория.docx |
| Тип | Документы #104785 |
| страница | 1 из 4 |
 С этим файлом связано 2 файл(ов). Среди них: макроэкономика лекции.doc, БД. Методичка #2..doc. С этим файлом связано 2 файл(ов). Среди них: макроэкономика лекции.doc, БД. Методичка #2..doc.  Показать все связанные файлы Подборка по базе: Вопрос N1 Кинематика материальной точки Радиус-вектор скорость и, Лекция температура, влажность, скорость движения воздуха, давлен, Задание № 2 — кинематика точки.docx, Отражение относительно точки.doc, Кинематика точки.Апазов А.А.ПБ 306-91.docx, Правовые основы материальной составляющей трудовых отношений — к, 1 кинематика.pdf, Федеральный закон от 12 июля 1999 г N 161 ФЗ О материальной отве, Манас — энциклопедия материальной и духовной культуры кыргызског, Использование компьютерной техники и современного программного о Показать все связанные файлы Подборка по базе: Вопрос N1 Кинематика материальной точки Радиус-вектор скорость и, Лекция температура, влажность, скорость движения воздуха, давлен, Задание № 2 — кинематика точки.docx, Отражение относительно точки.doc, Кинематика точки.Апазов А.А.ПБ 306-91.docx, Правовые основы материальной составляющей трудовых отношений — к, 1 кинематика.pdf, Федеральный закон от 12 июля 1999 г N 161 ФЗ О материальной отве, Манас — энциклопедия материальной и духовной культуры кыргызског, Использование компьютерной техники и современного программного оЧасть 1. Вопросы к экзамену по физике Кинематика материальной точки. Радиус-вектор, скорость и ускорение. Нормальная и тангенциальная составляющие ускорения. Радиус кривизны траектории. Кинематика вращательного движения. Угловые скорость и ускорение. Связь линейных и угловых характеристик движения. 1.Кинематика материальной точки.
Радиус кривизны представляет собой радиус окружности, которая сливается в данном месте с кривой на бесконечно малом её участке. Центром такой окружности называется центром кривизны для данной точки кривой. Система отсчёта -совокупность системы координат и часов, связанных с телом отсчёта.Чаще используют декартову с.к. Тело отсчёта-произвольно выбранное тело относительно которого определяется положение другого тела.движение мат. точк и полносью определено в пространстве,если декартовы координаты заданы в завмсимости от времени r=r(t) 2.Кинематика вращательного движения. Угловые скорость и ускорение.
2. Инерциальные системы отсчета. Понятия силы и инертной массы. Законы динамики. Силы в природе. Фундаментальные взаимодействия. Свойства сил упругости и тяготения. Свойства сил трения. Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой справедлив первый закон Ньютона(закон инерции): все свободные тела (то есть такие, на которые не действуют внешние силы или действиеэтих сил компенсируется) движутся прямолинейно и равномерно или покоятся[1]. Инертность — стремление тела сохранять состояние покоя или равномерного прямолинейного движения. Сила — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Сила считается заданной, если указано её численное значение, направление и точка приложение. Инертная масса — это масса, которая фигурирует во втором законе Ньютона и характеризует инертные свойства тела. Первый закон Ньютона: Всякое тело в инерциальной системе отсчёта, находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние. Второй закон Ньютона: Ускорение тела прямопропорц. действ. на него силы F и обратно пропорц. массе Третий закон Ньютона: Силы, с которой тела действуют друг на друга, равны по модулю и противоположны по направлению: F12=-F21. Си́ла упру́гости — сила, возникающая при деформации тела и противодействующая этой деформации.Сила упругости вычисляется по закону Гука, F=-kx, где k — жёсткость пружины. Закон всемирного тяготения: Все тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними Гравитационная постоянная – это коэффициент пропорциональности G называется Трение – один из видов взаимодействия тел. Оно возникает при соприкосновении двух тел. Силами сухого трения называют силы, возникающие при соприкосновении двух твердых тел при отсутствии между ними жидкой или газообразной прослойки. Сухое трение, возникающее при относительном покое тел, называют трением покоя. Сила трения покоя всегда равна по величине внешней силе и направлена в противоположную сторону Сила трения покоя не может превышать некоторого максимального значения (Fтр)max. Если внешняя сила больше (Fтр)max, возникает относительное проскальзывание. Силу трения в этом случае называют силой трения скольжения. При движении твердого тела в жидкости или газе возникает силa вязкого трения. Сила вязкого трения значительно меньше силы сухого трения. Она также направлена в сторону, противоположную относительной скорости тела. При вязком трении нет трения покоя. Силы трения возникают и при качении тела. Однако силы трения качения обычно достаточно малы. При решении простых задач этими силами пренебрегают. 3. Центр инерции. Закон сохранения импульса системы материальных точек. Центр масс ( центр ине́рции , барице́нтр ) в механике — это геометрическая точка , характеризующая движение тела или системы частиц как целого . Положение центра масс (центра инерции) в классической механике определяется следующим образом: — радиус—вектор центра масс, — радиус-вектор i-й точки системы, Для случая непрерывного распределения масс: — суммарная масса системы, Центр масс, таким образом, характеризует распределение массы по телу или системе частиц. В замкнутой системе тел векторная сумма импульсов всех тел (импульс p∑→ системы), входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой: Если импульс одного тела увеличился, то это означает, что у какого-то другого тела (или нескольких тел) в этот момент импульс уменьшился ровно на такую же величину. Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона. На практике закон сохранения импульса может применяться в следующих случаях: Если на систему не действуют внешние силы или действие скомпенсировано. Тогда справедлив закон сохранения импульса в векторном виде, и он выполняется в проекциях на любую ось. Если на систему не действуют внешние силы вдоль определенного направления или в этом направлении их действие скомпенсировано. Тогда выполняется закон сохранения импульса только на ось, выбранную вдоль этого направления. Если на систему действуют конечные по величине внешние силы, но за очень малое время они не успевают существенно изменить импульс системы. Обычно в таких случаях в тексте задачи можно увидеть слова «сразу после», которые означают, что быстрые процессы уже закончились, а медленные еще не начались. Если под действием силы F происходит движение и тело перемещается на величину S, то говорят, что сила совершает работу. Работа – скалярная физическая величина, равная произведению проекции силы Fs на направление перемещения на перемещение S. Эта формула справедлива для прямолинейного движения при Fs= const, а также когда угол между вектором силы и перемещением не изменяется. Учитывая, что Fs = F·cos выражению (4.1) можно придать вид: Другими словами, работу можно представить как скалярное произведение векторов и . Из формулы (4.2) видно, что работа может иметь как положительное, так и отрицательное значение. Когда cos >0 (a – острый угол), работа положительна (А>0), при cos Полем сил называют область пространства, в каждой точке которого на помещённую туда частицу действует сила, закономерно меняющаяся от точки к точке. Примером может служить поле силы тяжести Земли или поле сил сопротивления в потоке жидкости (газа). Потенциальным называется поле, работа которого при переходе из одной точки поля в другую не зависит от формы траектории. Потенциальными являются поле силы тяжести и электростатическое поле. Поле центральных сил. Примером центрального силового поля, т.е. такого, в котором силы действуют вдоль прямой, соединяющей центры взаимодействующих масс, является поле тяготения. При движении тела ( материальной точки, системы ) в поле тяготения силы, действующие со стороны поля, совершают работу. Так как величина силы зависит от положения тела, то величина работы определяется только начальным и конечным положениями системы и не зависит от формы траектории, по которой происходило перемещение этого тела. В этом легко убедиться, рассчитав работу сил тяготения по перемещению некоторой массы, начальное положение которой определяется радиус-вектором r1, a конечное — радиус-вектором r2. Потенциальная энергия системы . Потенциальная энергия — часть общей механической энергии системы, зависящая от взаимного расположения частиц, составляющих эту систему, и от их положений во внешнем силовом поле (например, гравитационном; см. Поля физические) . Потенциальная энергия упругой деформации. Потенциальной энергией деформации называется энергия, которая накапливается в теле при его упругой деформации. При этом точка приложения внешней силы перемещается, потенциальная энергия положения груза убывает на величину, которая численно равна работе, совершённой внешней силой. Таким образом, потенциальная энергия упругой деформации U равна работе внешней силы А. Потенциальная энергия в поле тяготения . Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой: Е = mgh Потенциальная энергия характеризует как минимум два тела или положение тела во внешнем поле. Кинетическая энергия характеризуется скоростью; потенциальная — взаиморасположением тел. |