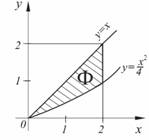
Независимо друг от друга выбираются две точки на окружности (5 видео)

Геометрическая вероятность

Пример №1 . Из промежутка [0; 2] наудачу выбраны два числа x и y. Найдите вероятность того, что эти числа удовлетворяют неравенствам x 2 ≤ 4y ≤ 4x.
Решение. Испытание состоит в случайном выборе из промежутка [0; 2] пары чисел x и y. Будем это интерпретировать как выбор наудачу точки M(x;y) из множества всех точек квадрата, сторона которого равна двум. Рассмотрим фигуру Ф, представляющую собой множество всех точек квадрата, координаты которых удовлетворяют системе неравенств x 2 ≤ 4y ≤ 4x. Интересующее событие происходит тогда и только тогда, когда выбранная точка M(x;y) принадлежит фигуре Ф.

По формуле (8) искомая вероятность равна отношению площади фигуры Ф к площади квадрата:

Пример №2 . Двое договорились о встрече в определенном месте. Каждый из них приходит в условленное место независимо друг от друга в случайный момент времени из [0;T] и ожидает не более чем время . Какова вероятность встречи на таких условиях?

Решение. Обозначим через x время прихода первого в условленное место, а через y — время прихода туда второго лица. Из условия вытекает, что x и y независимо друг от друга пробегают промежуток времени [0;T]. Испытание состоит в фиксации времени прихода указанных лиц к месту встречи. Тогда пространство элементарных исходов данного испытания интерпретируется как совокупность всех точек M(x;y) квадрата Ω=. Интересующее нас событие A — “встреча произошла” наступает в том и только том случае, когда выбранная точка M(x;y) окажется внутри фигуры Ф, представляющей собой множество всех точек квадрата, координаты которых удовлетворяют неравенству |x – y| ≤ t. По формуле (8) искомая вероятность
представляет собой отношение площади фигуры Ф к площади квадрата Ω:

Пример №3 . На отрезке l наугад выбраны две точки.
P(0 k-l

Пример №4 . В круг радиуса r случайным образом брошена точка так, что любое ее расположение в круге равновозможно. Найти вероятность того, что она окажется внутри находящегося в круге квадрата со стороной a.
Решение. Вероятность того, что точка окажется внутри лежащего в круге квадрата со стороной а будет равна отношению площади квадрат к площади круга.
Площадь квадрата: Sкв = a 2 .
Площадь круга: S = πr 2
Тогда вероятность составит: p = Sкв / S = a 2 / πr 2

Пример №5 . С промежутке [0, 4] выбирают наугад два действительных числа. Найдите вероятность того, что их сумма будет больше 4, а произведение — меньше 4.
Решение.
Всего чисел 5: 0,1,2,3,4. Вероятность их появления p=1/5 = 0.2
а) вероятность того, что их сумма будет больше 4
Всего количество таких исходов равно 8:
1+4, 2+3, 2+4, 3+4 и 4+1, 3+2, 4+2, 4+3
P = 0.2*0.2*8 = 0.32
б) произведение — меньше 4.
Всего количество таких исходов равно 13:
0*1, 0*2, 0*3, 0*4, 1*1, 1*2,1*3 и 1*0, 2*0, 3*0, 4*0, 2*1, 3*1
P = 0.2*0.2*13 = 0.52

Задачи для самостоятельного решения
4.3. После бури на участке между 40-м и 70-м километрами телефонной линии произошел обрыв провода. Какова вероятность того, что разрыв произошел между 45-м и 50-м километром линии? (Вероятность обрыва провода в любом месте считать одинаковой).
Ответ: 1/6.

4.4. В круг радиуса r наугад брошена точка. Найдите вероятность того, что эта точка окажется внутри вписанного в данный круг правильного треугольника.
Ответ:

4.5. Найдите вероятность того, что сумма двух случайно выбранных чисел из промежутка [-1; 1] больше нуля, а их произведение отрицательно.
Ответ: 0;25.

4.6. Во время боевой учебы н-ская эскадрилья бомбардировщиков получила задание атаковать нефтебазу “противника”. На территории нефтебазы, имеющей форму прямоугольника со сторонами 30 и 50 м, находятся четыре круглых нефтебака диаметром 10 м каждый. Найдите вероятность прямого поражения нефтебаков бомбой, попавшей на территорию нефтебазы, если попадание бомбы в любую точку этой базы равновероятно.
Ответ: π/15.

4.7. Два действительных числа x и y выбираются наудачу так, что сумма их квадратов меньше 100. Какова вероятность, что сумма квадратов этих чисел окажется больше 64?
Ответ: 0;36.

4.8. Двое друзей условились встретиться между 13 и 14 часами. Пришедший первым ждет второго в течение 20 минут, после чего уходит. Определите вероятность встречи друзей, если моменты их прихода в указанном промежутке времени равновозможны.
Ответ: 5/9.

4.9. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов равновозможно в течение данных суток. Определите вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода равно одному часу, а второго — двум часам.
Ответ: ≈ 0;121.

4.10. Наудачу взяты два положительных числа x и y, каждое из которых не превышает двух. Найдите вероятность того, что произведение x · y будет не больше единицы, а частное y/x не больше двух.
Ответ: ≈ 0;38.

4.11. В области G, ограниченной эллипсоидом , наудачу зафиксирована точка. Какова вероятность того, что координаты (x; y; z) этой точки будут удовлетворять неравенству x 2 +y 2 +z 2 ≤4?
Ответ: 1/3.

4.12. В прямоугольник с вершинами R(-2;0), L(-2;9), M (4;9), N (4;0) брошена точка. Найдите вероятность того, что ее координаты будут удовлетворять неравенствам 0 ≤ y ≤ 2x – x 2 +8.
Ответ: 2/3.

4.13. Область G ограничена окружностью x 2 + y 2 = 25, а область g — этой окружностью и параболой 16x — 3y 2 > 0. Найдите вероятность попадания в область g.
Ответ: ≈ 0;346.

4.14. Наудачу взяты два положительных числа x и y, каждое из которых не превышает единицы. Найдите вероятность того, что сумма x + y не превышает единицы, а произведение x · y не меньше 0,09.
Ответ: ≈ 0;198.

Содержание

Вычисление геометрической вероятности в случае ограниченной и неограниченной области
Независимо друг от друга выбираются две точки на окружности
Невероятность
Мат ожидание бросков мячика в воду
Расскажите школьникам о коктейлях
Продолжение
Секта
Фифти-фифти
📺 Видео

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Вычисление геометрической вероятности в случае ограниченной и неограниченной области

ВЫЧИСЛЕНИЕ ГЕОМЕТРИЧЕСКОЙ ВЕРОЯТНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ И НЕОГРАНИЧЕННОЙ ОБЛАСТИ

научный руководитель канд. пед. наук

Сибирский федеральный университет

В различных разделах науки и техники нередко возникают ситуации, когда результат каждого из многих проводимых опытов заранее предугадать невозможно, однако можно исследовать закономерности, возникающие при проведении серии опытов. Нельзя, например, точно сказать, какая сторона монеты окажется сверху при данном броске: герб или цифра – но при большом количестве бросков число выпадений герба приближается к половине количества бросков; нельзя заранее предсказать результат одного выстрела из данного орудия по данной цели, но при большом числе выстрелов частота попадания приближается к некоторому постоянному числу. Исследование вероятностных закономерностей массовых однородных явлений составляет предмет теории вероятностей.

Теория вероятностей – сравнительно молодая ветвь математики. Ее развитие как самостоятельной науки началось с переписки Паскаля и Ферма в 1654 году. Однако раньше уже Кардано (1501 – 1576) и Галилей (1564 – 1642) правильно решали специальные теоретико-вероятностные задачи.

Мысль о том, что законы природы проявляются через множество случайных событий, подробно изложил Лукреция Кара в поэме «О природе вещей». В 1658 году появилась книга Христиана Гюйгенса (1629 — 1695) «О расчетах в азартных играх».
С работой Гюйгенса непосредственно связана основная работа Якоба Бернулли
(1654 – 1705) «Искусство догадок». Работы Абрахама де Муавра (1667 – 1754)
«Об измерении случайности, или о вероятностях результатов в азартных играх», опубликованы в 1711 году. В Лондоне уже с 1592 года составлялись таблицы смертности и вопросы страхования. На основе этих записей Джон Граунт
(1620 – 1674) в 1662 году впервые составил таблицы вероятности смерти как функции возраста. Несколькими годами позднее Ван Худде и Ван де Витт в Голландии, проделав аналогичные расчеты, использовали их для вычисления пожизненной ренты. Подробнее эти вопросы в 1693 году были изложены Галлеем.

Основным понятием классической теории вероятностей является случайное событие. Из анализа математической литературы известны следующие виды вероятности случайного события – это классическая, статистическая и геометрическая вероятности. Отметим недостатки некоторых подходов к определению вероятностей: классический способ не применим к бесконечным множествам событий (исходов) и предполагает наличие полной группы событий, то есть идеальной ситуации; статистическое определение предполагает неоднозначность статистической вероятности, значения которой колеблется около какого-то теоретического числа.

Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности. Геометрическая вероятность – вероятность попадания точки в область (отрезок, часть плоскости или пространства). Все дальнейшие рассуждения будем вести, опираясь на точку зрения , , .

В задачах по нахождению геометрической вероятности будем испытание интерпретировать как случайный выбор точки в некоторой области D, а событие А – как попадание выбранной точки в некоторую подобласть G области D. При этом требуется, чтобы все точки области D имели одинаковую возможность быть выбранными.

Обозначим меру (длину, площадь, объем) области через m. При этом вероятность попадания точки, брошенной наудачу в область G — часть области D, равна отношению мер областей G и D, соответственно равных m(G) и m(D).Формула геометрической вероятности в этом случае имеет вид: P(A) = m(G) / m(D).

В случае классического определения вероятность достоверного (невозможного) события равна единице (нулю); справедливы и обратные утверждения (например, если вероятность события равна нулю, то событие невозможно). В случае геометрического определения вероятности обратные утверждения не имеют места. Например, вероятность попадания брошенной точки в одну определенную точку области D равна нулю, однако это событие может произойти, и, следовательно, не является невозможным.

Приведем рассмотренные нами задачи, иллюстрирующие подходы к нахождению геометрической вероятности случайного события в случае ограниченной и неограниченной областей.

Задача 1. Две точки независимо друг от друга наудачу выбираются на отрезке
[0;1]. Найти вероятность того, что частное от деления координаты первой точки на координату второй точки больше 0,5.

1. Пусть и — координаты первой и второй точек, выбранных на [0;1]. Каждой паре () вещественных чисел соответствует точка квадрата
D = <(х, у): > на плоскости XOY, а пространство элементарных исходов совпадает с квадратом D.

2. Проверим равновозможность элементарных исходов. Она гарантирована методикой проведения случайного эксперимента, так как обе точки выбираются на отрезке наудачу и ни один из участков квадрата не является более предпочтительным, чем другой равный ему по площади.

3. Выделим те элементарные (благоприятные) исходы, которые приводят к наступлению интересующего нас события. Благоприятным исходам А = <> 0,5> соответствует та часть области D, в которой частное от деления координаты первой точки на координату второй точки больше 0,5 , то есть область
G = <(x, y): > 0,5>D (рис. 1). Причем мерами областей D и G в условиях нашей задачи являются их площади.

4. Находим площадь S(D) области D. Очевидно, что S(D) = 1, как площадь квадрата со стороной длины равной 1.

5. Находим площадь S(G) области G. Имеем:.

6. Тогда, согласно геометрическому определению вероятности:

Задача 2. Плоскость разбита прямыми на квадратные клетки со стороной а. Клетки пронумерованы при помощи пар целых чисел (m, n) (при этом у соседней справа клетки будет номер (m + 1, n), а у соседней сверху клетки будет номер
(m, n + 1)). Найти вероятность того, что брошенная наудачу на плоскость монета радиуса целиком попадет в какую-нибудь клетку, для которой m2 – n2 кратно четырем.

1. Определим пространство элементарных исходов. В данном случае им является любая из равных прямоугольных ячеек, которые содержат равные части множества благоприятных исходов G равные части его дополнения до всей плоскости. Обозначим такую ячейку символом D. Чтобы найти D, заметим, что если некоторая клетка (m, n), удовлетворяет требуемому условию, то ему удовлетворяют и клетки (m + 2, n), (m – 2, n), (m, n + 2), (m, n – 2), то есть имеет место периодичность по горизонтали с периодом 2 и по вертикали с периодом 2. Поэтому в качестве ячейки D можно взять область размером 2 на 2, составленную из клеток (0,0), (0,1), (1,0), (1,1) (рис. 2).

2. Проверим равновозможность элементарных исходов. Она гарантирована методикой проведения случайного эксперимента, поскольку, как сказано в условии задачи, монета бросается наудачу.

3. Опишем те элементарные исходы, которые приводят к наступлению интересующего нас события: m2 – n2 делится на четыре в клетках (0,0) и (1,1). Для того чтобы монета оказалась внутри некоторой клетки, необходимо и достаточно, чтобы центр монеты находился в одной из точек, расположенных внутри клетки на расстоянии большем r от границы этой клетки. На рисунке 2 изображена ячейка D и заштрихована область благоприятных исходов .

4. Находим площадь S(D) ячейки D. Имеем S(D) = 4а2, т. к. имеется четыре квадратные ячейки со стороной а.

5. Находим площадь S(G) области . Имеем S(G) = 2(а – 2r)2, так как нас интересуют в условиях задачи две ячейки, область G в которых является квадратом со стороной (а – 2r).

6. Искомая вероятность равна:

Подводя итог, отметим, что подходы к нахождению геометрической вероятности для ограниченной и неограниченной областей имеют следующие особенности:

− при нахождении геометрической вероятности попадания точки в область G, принадлежащей ограниченной области D, за пространство элементарных исходов берется область D, множество благоприятных исходов представлено областью G;

− в случае вычисления геометрической вероятности нахождения точки в неограниченной области G принадлежащей области D, сначала производится деление области на равные прямоугольные ячейки и выбирается область ячеек, которые содержат равные части области G и равные части ее дополнения. Далее отбираются благоприятные исходы, множество которых совпадает с областью G, принадлежащей целиком области D.

Видео:Окружность данного радиуса, проходящей через две заданные точкиСкачать

Независимо друг от друга выбираются две точки на окружности

Ященко 36 вариантов (Национальное образование, drive.google.com/file/d/1hPI-uuC-xJpeZh2Jeq6Liv. )
Вариант 36, задание 10

В викторине участвуют 15 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых 8 играх победила команда А. Какова вероятность того, что эта команда выиграет девятый раунд?

Два способа решения (2:14:20 и 2:27:34)

Видео:Теория вероятностей | Математика TutorOnlineСкачать

Невероятность

Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число N. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.

Ответы из сборника 50 вариантов:
N Вероятность
4 0,5
5 0,56
6 0,58
7 0,42
8 0,28
9 0,42

Видео:Математика без Ху!ни. Теория вероятностей, комбинаторная вероятность.Скачать

Мат ожидание бросков мячика в воду

Видео:Геометрическая вероятностьСкачать

Расскажите школьникам о коктейлях

попалось на глаза.

Видео:Теорема о числе точек пересечения двух окружностейСкачать

Продолжение

29 апреля девятиклассники матвертикали имели возможность еще раз написать контрольную по твисту.

Формулировку девятой задачи поменяли и теперь она выглядит так:

Перед скачками обязательно проводится взвешивание жокеев. В заезде участвуют четыре жокея – Андрей, Борис, Владимир и Григорий. При взвешивании выяснилось, что вес у всех разный и что Андрей легче Владимира, а Владимир легче Григория. Какова вероятность того, что Борис окажется тяжелее Григория?

Выберите ответ. При желании напишите, как вы его получили.

Вопрос: Ответ

1. 1/2	2	(40%)
2. 1/3	2	(40%)
4. 1/5	1	(20%)
5. 1/6	(0%)
Всего:	5

Видео:Сердобольская М.Л. - Теория вероятностей. Семинары - 3. Геометрическая вероятностьСкачать

Секта

Недавно состоялся семинар, на котором руководители ресурсных центров матвертикали рассказывали учителям, как нужно объяснять недорослям решения проводившейся в девятых классах в начале месяца контрольной работы по теории вероятностей.

читать дальше

0:00 Вступление
1:00 Задача №1
3:50 Задача №2
7:20 Задача №3
8:27 Задача №4
11:25 Задача №5
13:00 Задача №6
14:58 Задача №7
19:10 Задача №8
23:52 Задача №9
42:02 Задача №10
53:30 Ответы на вопросы
vertical.sch-int.ru/https-vertical-sch-int-ru-s.

P.S. При обсуждении девятой задачи полезно предложить школьникам исследовать зависимость вероятности n+1-ой победы от количества оставшихся в строю неудачников, поговорить о парадоксах и странностях окружающего их мира.
P.P.S. Математика — це москальська лженаука!

Видео:Задача про две вневписанные окружности | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать

Фифти-фифти

В летнем лагере проводится турнир по настольному теннису по круговой системе, то есть
каждый участник играет по одному разу со всеми другими. В каждой встрече побеждает тот, кто
играет лучше, при этом нет двух участников, играющих одинаково хорошо. Очерёдность игровых
пар определяется жребием. Известно, что Пётр выиграл в первых пяти своих встречах. Какова веро-
ятность того, что он выиграет и в следующей встрече тоже?

Авторское решение
Шестой соперник выиграет у Петра, только если он играет лучше, чем Пётр и пять его
предыдущих соперников. То есть он должен оказаться самым лучшим игроком среди
семи. В силу случайности порядка встреч вероятность этого равна 1/7. Следовательно, ве-
роятность выигрыша Петра равна 6/7.

Архив контрольных. 9 класс. Статистика. vertical.sch-int.ru/

Задача для самостоятельного решения
В летнем лагере проводится турнир по настольному теннису по круговой системе, то есть
каждый участник играет по одному разу со всеми другими. В каждой встрече побеждает тот, кто
играет лучше, при этом нет двух участников, играющих одинаково хорошо. Очерёдность игровых
пар определяется жребием. Известно, что Пётр принимает участие в турнире. Какова веро-
ятность того, что он выиграет в первой встрече?