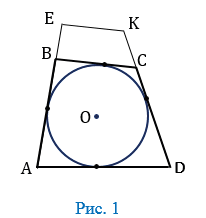
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность. На рисунке 1 четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
Теорема
| В любой треугольник можно вписать окружность. |
Доказательство
Дано: произвольный 
АВС.
Доказать: в АВС можно вписать окружность.
Доказательство:
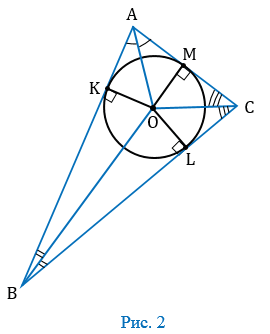
1. Проведем биссектрисы углов А, В и С, которые пересекутся в точке О (следствие из свойства биссектрис). Из точки О проведем перпендикуляры ОК, ОL и ОМ соответственно к сторонам АВ, ВС и СА (Рис. 2).
2. Точка О равноудалена от сторон АВС (свойство биссектрис), поэтому ОК = ОL = ОМ. Следовательно, окружность с центром О радиуса ОК проходит через точки К, L и М. Стороны АВС касаются этой окружности в точках К, L, М, т.к. они перпендикулярны к радиусам ОК, ОL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в АВС. Теорема доказана.
Замечание 1
| В треугольник можно вписать только одну окружность. |
Доказательство
Предположим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудален от сторон треугольника и, значит, совпадает с точкой О пересечения биссектрис треугольника, а радиус равен расстоянию от точки О до сторон треугольника. Следовательно, эти окружности совпадают, значит в треугольник можно вписать только одну окружность. Что и требовалось доказать.
Замечание 2
| Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности. |
Доказательство
На рисунке 2 мы видим, что АВС составлен из трех треугольников: АВО, ВСО и САО. Пусть АВ, ВС и АС основания треугольников АВО, ВСО и САО соответственно, тогда высотами данных треугольников окажутся отрезки ОК = ОL = ОМ = r ( r — радиус окружности с центром О). Следовательно, площади этих треугольников вычисляются по формулам: 
. Тогда, по свойству площадей, площадь треугольника АВС выражается формулой: 
, где 
— периметр АВС. Что и требовалось доказать.
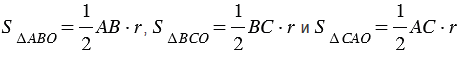
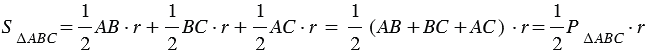
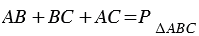
Замечание 3
| Не во всякий четырехугольник можно вписать окружность. |
Доказательство
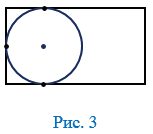
Рассмотрим, например, прямоугольник, у которого смежные стороны не равны, т.е. прямоугольник, не являющийся квадратом. В такой прямоугольник можно «поместить» окружность, касающуюся трех его сторон (Рис.3), но нельзя «поместить» окружность так, чтобы она касалась всех четырех его сторон, т.к. диаметр окружности меньше большей стороны прямоугольника т.е. нельзя вписать окружность. Что и требовалось доказать.
Если же в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:
| В любом описанном четырехугольнике суммы противоположных сторон равны. |
Доказательство
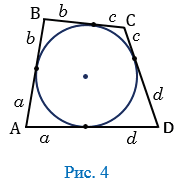
Рассмотрим четырехугольник АВСD, описанный около окружности (Рис. 4).
На рисунке 4 одинаковыми буквами обозначены равные отрезки касательных, т.к. отрезки касательных к окружности, проведенные из одной точки, равны. Тогда АВ + СD =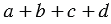 
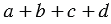
и ВС + АD = , следовательно, АВ + СD = ВС + АD.
Верно и обратное утверждение:
| Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность. |
Доказательство
Пусть в выпуклом четырехугольнике АВСD
АВ + СD = ВС + АD. (1)
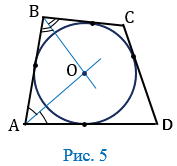
Точка О пересечения биссектрис углов А и В равноудалена от сторон АD, АВ и ВС (свойство биссектрис), поэтому можно провести окружность с центром О, касающуюся указанных трех сторон (Рис. 5).
Докажем, что эта окружность касается также стороны СD и, значит, является вписанной в четырехугольник АВСD.
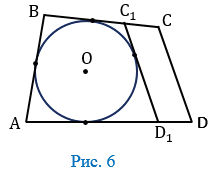
Предположим, что это не так. Тогда прямая СD либо не имеет общих точек с окружностью, либо является секущей. Рассмотрим первый случай (Рис. 6). Проведем касательную С1D1, параллельную стороне СD (С1 и D1 — точки пересечения касательной со сторонами ВС и АD).
Так как АВС1D1 — описанный четырехугольник, то по свойству его противоположных сторон
АВ + С1D1 = ВС1 + AD1. (2)
Но ВС1 = ВС — С1С, АD1 = АD — D1D, поэтому из равенства (2) получаем:
С1D1 + С1С + D1D = ВС + АD — АВ.
Правая часть этого равенства в силу (1) равна СD. Следовательно, приходим к равенству
т.е. в четырехугольник С1СDD1 одна сторона равна сумме трех других сторон. Но этого не может быть, т.к. к аждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон. Значит, наше предположение ошибочно. Аналогично можно доказать, что прямая CD не может быть секущей окружности. Следовательно, окружность касается стороны СD. Что и требовалось доказать.
Поделись с друзьями в социальных сетях:
Видео:В любой треугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
Не в каждый треугольник можно вписать окружность
Какие из следующих утверждений верны?
1) Около всякого треугольника можно описать не более одной окружности.
2) В любой треугольник можно вписать не менее одной окружности.
3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.
4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «Около всякого треугольника можно описать не более одной окружности.» — верно, oколо треугольника можно описать окружность, притом только одну.
2) «В любой треугольник можно вписать не менее одной окружности.» — верно, в любой треугольник можно вписать окружность.
3) «Центром окружности, описанной около треугольника, является точка пересечения биссектрис.» — неверно, центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров треугольника.
4) «Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.» — неверно, центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника.
Выражение «не более одной» означает, что окружностей не может быть больше одной. Выражение «не менее одной» означает, что окружностей не может быть меньше одной. В частности, «ровно одна окружность» удовлетворяет как условию «не более одной», так и условию «не менее одной».
Утверждение «В любой треугольник можно вписать не менее одной окружности» можно сформулировать так: «В любой треугольник можно вписать хотя бы одну окружность». Если бы это утверждение было неверным, это означало бы, что существуют треугольники, в которые нельзя вписать хотя бы одну окружность, но таких треугольников не существует, поэтому утверждение является верным.
Видео:Если в четырёхугольник можно вписать окружностьСкачать
Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов
Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.
В любой треугольник можно вписать окружность, причем только одну.
Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.
Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?
В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.
Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.
Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.
— радиус окружности, вписанной в треугольник.
Есть и еще одна формула, применяемая в основном в задачах части :
где — стороны треугольника, — радиус описанной окружности.
Для любого треугольника верна теорема синусов:
Ты нашел то, что искал? Поделись с друзьями!
. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .
В ответ запишем .
. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.
По теореме синусов,
Получаем, что . Угол — тупой. Значит, он равен .
. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.
Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .
🌟 Видео
№700. Докажите, что в любой ромб можно вписать окружность.Скачать
В любой четырёхугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
В любой прямоугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать
Вписанная и описанная окружность - от bezbotvyСкачать
Окружность вписанная в треугольник и описанная около треугольника.Скачать
Треугольник и окружность #shortsСкачать
В любой ромб можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать
8 класс, 38 урок, Вписанная окружностьСкачать
Любой прямоугольник можно вписать в окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать
Построить описанную окружность (Задача 1)Скачать
№696. Докажите, что если в параллелограмм можно вписать окружность, то этот параллелограмм — ромб.Скачать
Строим вписанную в данный треугольник окружность (Задача 2).Скачать
Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать
Свойство четырехугольника, в который можно вписать окружностьСкачать
