Алгоритм построения треугольника:
Начерти угол, отложить на одном из лучей угла отрезок, равный длине одной из сторон треугольника. Отложить на другом луче угла отрезок, равный длине второй стороне треугольника. Провести отрезок, соединяющий отрезки отложенные на лучах угла. Отметить вершины треугольника и присвоить им имена-буквы.
Алгоритм построения треугольника:
Начерти угол, отложить на одном из лучей угла отрезок, равный длине одной из сторон треугольника. Отложить на другом луче угла отрезок, равный длине второй стороне треугольника. Провести отрезок, соединяющий отрезки отложенные на лучах угла. Отметить вершины треугольника и присвоить им имена-буквы.
Алгоритм построения треугольника:
Начерти угол, отложить на одном из лучей угла отрезок, равный длине одной из сторон треугольника. Отложить на другом луче угла отрезок, равный длине второй стороне треугольника. Провести отрезок, соединяющий отрезки отложенные на лучах угла. Отметить вершины треугольника и присвоить им имена-буквы.
- Блок-схема: примеры, элементы, построение. Блок-схемы алгоритмов
- Что такое алгоритм?
- Особенности алгоритма
- Словесная запись
- Запись в графической форме
- Запись на языках программирования
- Блок-схемы
- Основные правила составления блок-схемы
- Линейный тип алгоритмов
- Разветвляющиеся алгоритмы
- Циклический алгоритм
- Циклы со счетчиками
- Циклы с предусловием
- Что такое цикл с постусловием?
- Сложные циклы
- Решение задач с блок-схемами
- Треугольник Паскаля — формула, свойства и применение
- Основная формула
- История открытия
- Отличительные черты
- Общие свойства
- Секреты треугольника
- Полномочия двойки
- Силы одиннадцати
- Совершенные квадраты
- Комбинаторные варианты
- Действия с биномами
Видео:Алгоритмы решения задач. Правило треугольника.Скачать

Блок-схема: примеры, элементы, построение. Блок-схемы алгоритмов
В этой статье будут рассмотрены примеры блок-схем, которые могут встретиться вам в учебниках по информатике и другой литературе. Блок-схема представляет собой алгоритм, по которому решается какая-либо задача, поставленная перед разработчиком. Сначала нужно ответить на вопрос, что такое алгоритм, как он представляется графически, а самое главное – как его решить, зная определенные параметры. Нужно сразу отметить, что алгоритмы бывают нескольких видов.
Видео:Алгоритмы. Попадание точки в треугольникСкачать

Что такое алгоритм?
Это слово ввел в обиход математик Мухаммед аль-Хорезми, который жил в период 763-850 года. Именно он является человеком, который создал правила выполнения арифметических действий (а их всего четыре). А вот ГОСТ от 1974 года, который гласит, что:
Алгоритм – это точное предписание, которое определяет вычислительный процесс. Причем имеется несколько переменных с заданными значениями, которые приводят расчеты к искомому результату.
Алгоритм позволяет четко указать исполнителю выполнять строгую последовательность действий, чтобы решить поставленную задачу и получить результат. Разработка алгоритма – это разбивание одной большой задачи на некую последовательность шагов. Причем разработчик алгоритма обязан знать все особенности и правила его составления.
Видео:Как Собрать Пираминкс | Самый простой способ 2023Скачать

Особенности алгоритма
Всего можно выделить восемь особенностей алгоритма (независимо от его вида):
- Присутствует функция ввода изначальных данных.
- Есть вывод некоего результата после завершения алгоритма. Нужно помнить, что алгоритм нужен для того, чтобы достичь определенной цели, а именно – получить результат, который имеет прямое отношение к исходным данным.
- У алгоритма должна быть структура дискретного типа. Он должен представляться последовательными шагами. Причем каждый следующий шаг может начаться только после завершения предыдущего.
- Алгоритм должен быть однозначным. Каждый шаг четко определяется и не допускает произвольной трактовки.
- Алгоритм должен быть конечным – необходимо, чтобы он выполнялся за строго определенное количество шагов.
- Алгоритм должен быть корректным – задавать исключительно верное решение поставленной задачи.
- Общность (или массовость) – он должен работать с различными исходными данными.
- Время, которое дается на решение алгоритма, должно быть минимальным. Это определяет эффективность решения поставленной задачи.
А теперь, зная, какие существуют блок-схемы алгоритмов, можно приступить к рассмотрению способов их записи. А их не очень много.
Видео:ПРОСТОЙ СПОСОБ КАК СОБРАТЬ ПИРАМИДКУ РУБИКА(МЕФФЕРТА)Скачать

Словесная запись
Такая форма, как правило, применяется при описании порядка действий для человека: «Пойди туда, не знаю куда. Принеси то, не знаю что».
Конечно, это шуточная форма, но суть понятна. В качестве примера можно привести еще, например, привычную запись на стеклах автобусов: «При аварии выдернуть шнур, выдавить стекло».
Здесь четко ставится условие, при котором нужно выполнить два действия в строгой последовательности. Но это самые простые алгоритмы, существуют и более сложные. Иногда используются формулы, спецобозначения, но при обязательном условии – исполнитель должен все понимать.
Допускается изменять порядок действий, если необходимо вернуться, например, к предыдущей операции либо обойти какую-то команду при определенном условии. При этом команды желательно нумеровать и обязательно указывается команда, к которой происходит переход: «Закончив все манипуляции, повторяете пункты с 3 по 5».
Видео:Блок-схемы для начинающих (Блок схемы алгоритмов)Скачать

Запись в графической форме
В этой записи участвуют элементы блок-схем. Все элементы стандартизированы, у каждой команды имеется определенная графическая запись. А конкретная команда должна записываться внутри каждого из блоков обычным языком или математическими формулами. Все блоки должны соединяться линиями – они показывают, какой именно порядок у выполняемых команд. Собственно, этот тип алгоритма более подходит для использования в программном коде, нежели словесный.
Видео:9 класс, 15 урок, Решение треугольниковСкачать

Запись на языках программирования
В том случае, если алгоритм необходим для того, чтобы задачу решала программа, установленная на ПК, то нужно его записывать специальным кодом. Для этого существует множество языков программирования. И алгоритм в этом случае называется программой.
Видео:Самый подробный урок про Блок-схемы, Понимание, Чтение и Создание блок-схемСкачать

Блок-схемы
Блок-схема – это представление алгоритма в графической форме. Все команды и действия представлены геометрическими фигурами (блоками). Внутри каждой фигуры вписывается вся информация о тех действиях, которые нужно выполнить. Связи изображены в виде обычных линий со стрелками (при необходимости).
Для оформления блок-схем алгоритмов имеется ГОСТ 19.701-90. Он описывает порядок и правила создания их в графической форме, а также основные методы решения. В этой статье приведены основные элементы блок-схем, которые используются при решении задач, например, по информатике. А теперь давайте рассмотрим правила построения.
Видео:МОЙ РЕКОРД КУБИК РУБИКА ПИРАМИДКА (Pyraminx) / URAL OPEN 2022 В ЧЕЛЯБИНСКЕ. СОБРАЛ ЗА 3.71 сотую!Скачать

Основные правила составления блок-схемы
Можно выделить такие особенности, которые должны быть у любой блок-схемы:
- Обязательно должно присутствовать два блока – «Начало» и «Конец». Причем в единичном экземпляре.
- От начального блока до конечного должны быть проведены линии связи.
- Из всех блоков, кроме конечного, должны выходить линии потока.
- Обязательно должна присутствовать нумерация всех блоков: сверху вниз, слева направо. Порядковый номер нужно проставлять в левом верхнем углу, делая разрыв начертания.
- Все блоки должны быть связаны друг с другом линиями. Именно они должны определять последовательность, с которой выполняются действия. Если поток движется снизу вверх или справа налево (другими словами, в обратном порядке), то обязательно рисуются стрелки.
- Линии делятся на выходящие и входящие. При этом нужно отметить, что одна линия является для одного блока выходящей, а для другого входящей.
- От начального блока в схеме линия потока только выходит, так как он является самым первым.
- А вот у конечного блока имеется только вход. Это наглядно показано на примерах блок-схем, которые имеются в статье.
- Чтобы проще было читать блок-схемы, входящие линии изображаются сверху, а исходящие снизу.
- Допускается наличие разрывов в линиях потока. Обязательно они помечаются специальными соединителями.
- Для облегчения блок-схемы разрешается всю информацию прописывать в комментариях.
Графические элементы блок-схем для решения алгоритмов представлены в таблице:
Видео:Как собрать треугольник очень легкоСкачать
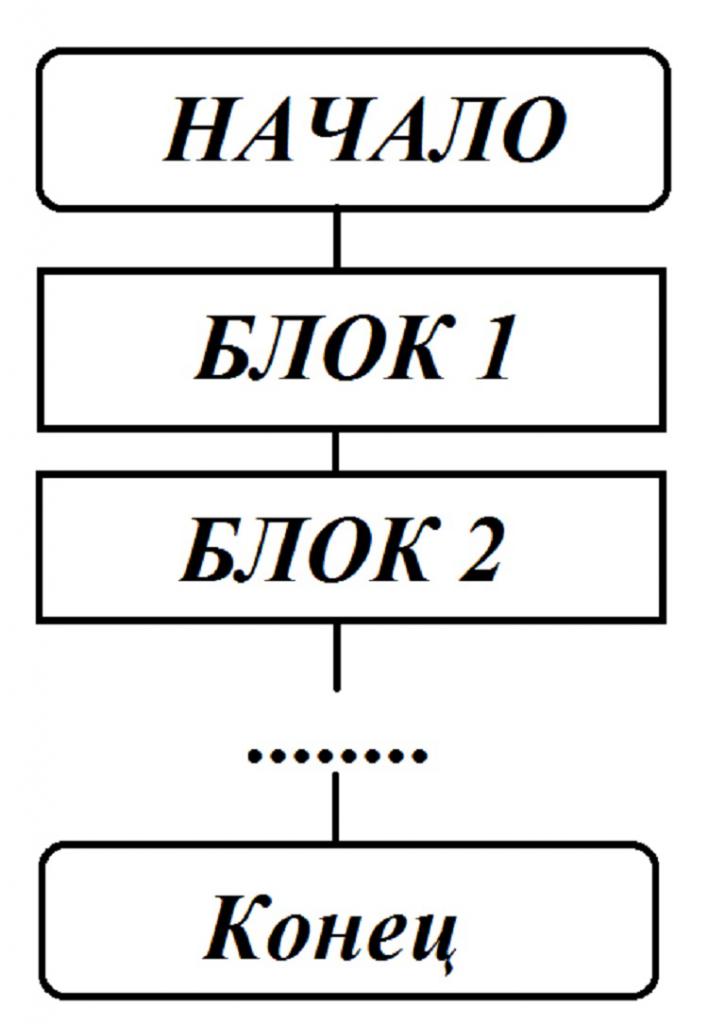
Линейный тип алгоритмов
Это самый простой вид, который состоит из определенной последовательности действий, они не зависят от того, какие данные вписаны изначально. Есть несколько команд, которые выполняются однократно и только после того, как будет сделана предшествующая. Линейная блок-схема выглядит таким образом:
Причем связи могут идти как сверху вниз, так и слева направо. Используется такая блок-схема для записи алгоритмов вычислений по простым формулам, у которых не имеется ограничений на значения переменных, входящих в формулы для расчета. Линейный алгоритм – это составная часть сложных процессов вычисления.
Видео:Как Быстро Собрать ПираминксСкачать

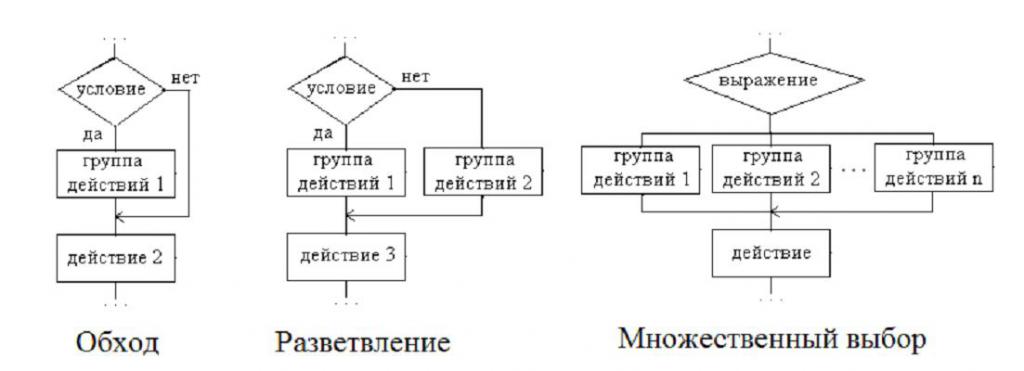
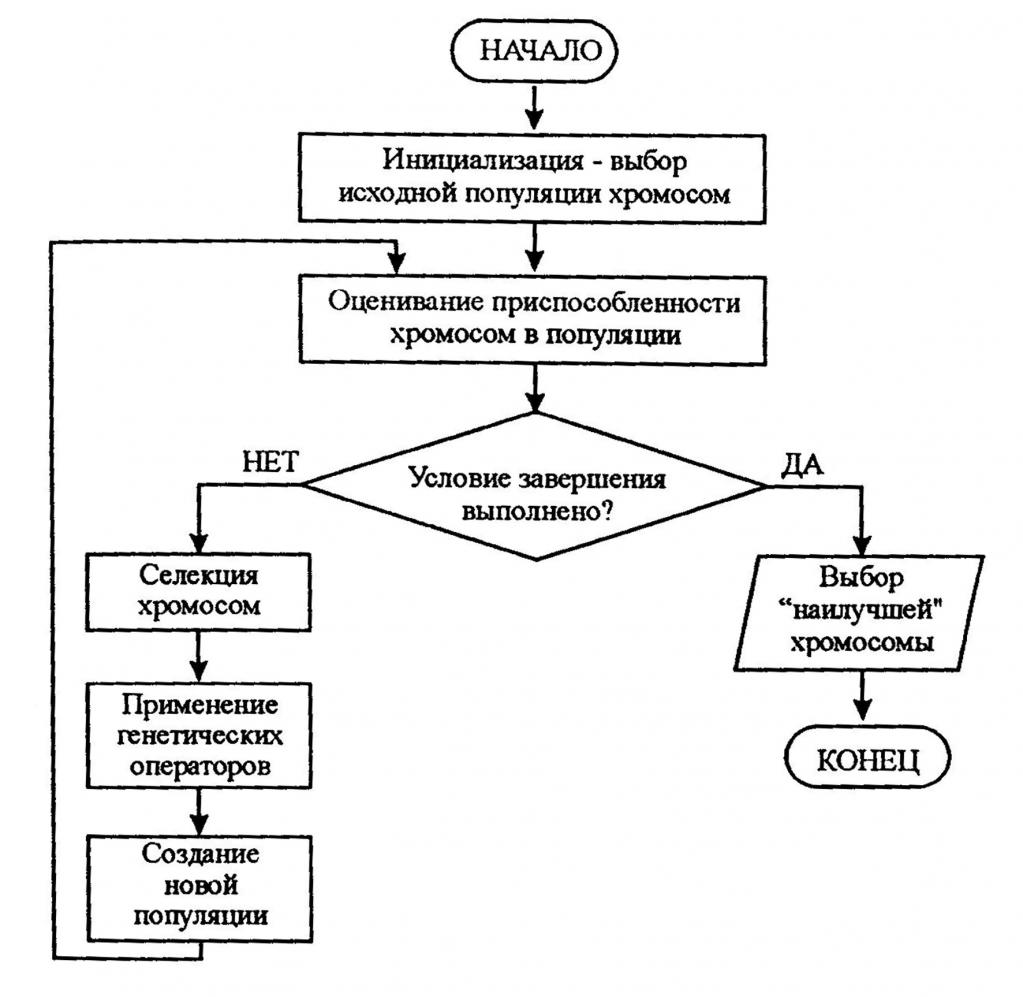
Разветвляющиеся алгоритмы
Блок-схемы, построенные по таким алгоритмам, являются более сложными, нежели линейные. Но суть не меняется. Разветвляющийся алгоритм – это процесс, в котором дальнейшее действие зависит от того, как выполняется условие и какое получается решение. Каждое направление действия – это ветвь.
На схемах изображаются блоки, которые называются «Решение». У него имеется два выхода, а внутри прописывается логическое условие. Именно от того, как оно будет выполнено, зависит дальнейшее движение по схеме алгоритма. Можно разделить разветвляющиеся алгоритмы на три группы:
- «Обход» – при этом одна из веток не имеет операторов. Другими словами, происходит обход нескольких действий другой ветки.
- «Разветвление» – каждая ветка имеет определенный набор выполняемых действий.
- «Множественный выбор» – это разветвление, в котором есть несколько веток и каждая содержит в себе определенный набор выполняемых действий. Причем есть одна особенность – выбор направления напрямую зависит от того, какие заданы значения выражений, входящих в алгоритм.
Это простые алгоритмы, которые решаются очень просто. Теперь давайте перейдем к более сложным.
Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Циклический алгоритм
Здесь все предельно понятно – циклическая блок-схема представляет алгоритм, в котором многократно повторяются однотипные вычисления. По определению, цикл – это определенная последовательность каких-либо действий, выполняемая многократно (более, чем один раз). И можно выделить несколько типов циклов:
- У которых известно число повторений действий (их еще называют циклами со счетчиком).
- У которых число повторений неизвестно – с постусловием и предусловием.
Независимо от того, какой тип цикла используется для решения алгоритма, у него обязательно должна присутствовать переменная, при помощи которой происходит выход. Именно она определяет количество повторений цикла. Рабочая часть (тело) цикла – это определенная последовательность действий, которая выполняется на каждом шаге. А теперь более детально рассмотрим все типы циклов, которые могут встретиться при составлении алгоритмов и решении задач по информатике.
Видео:Программирование ПЛК в ONI PLR Studio часть 2. Схема звезда - треугольникСкачать

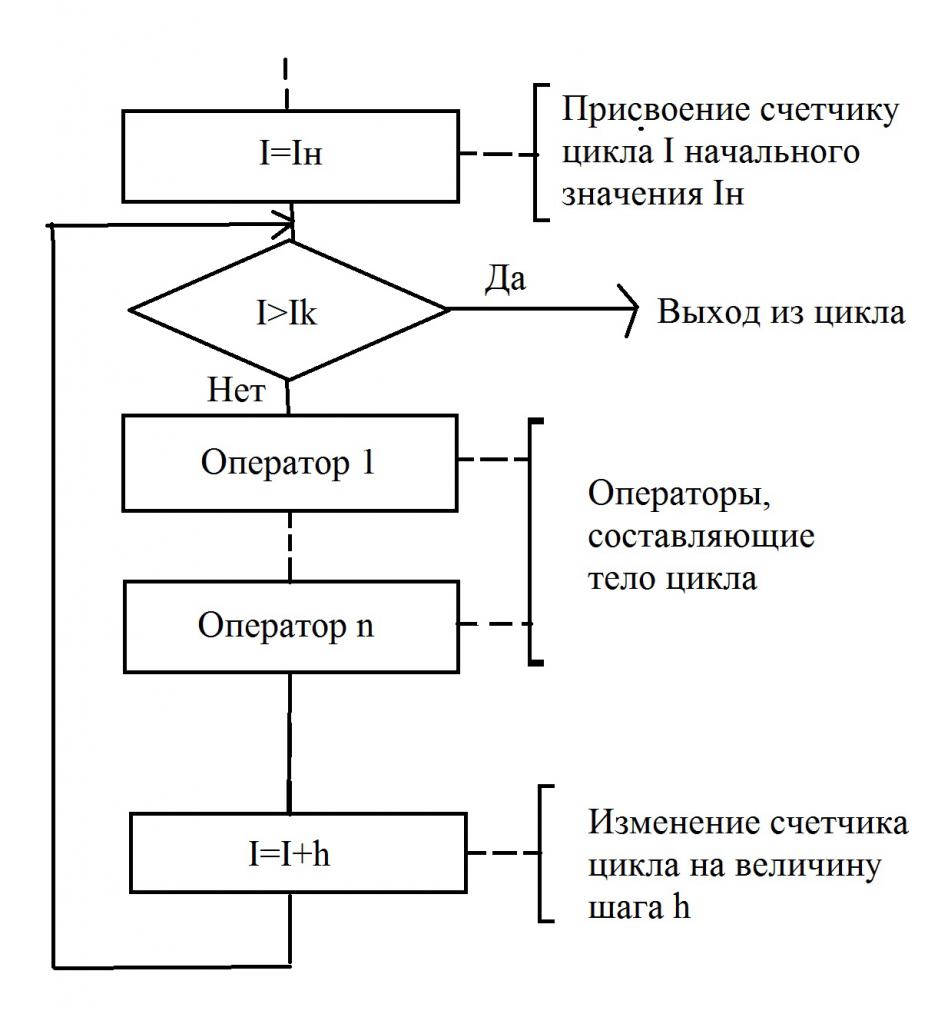
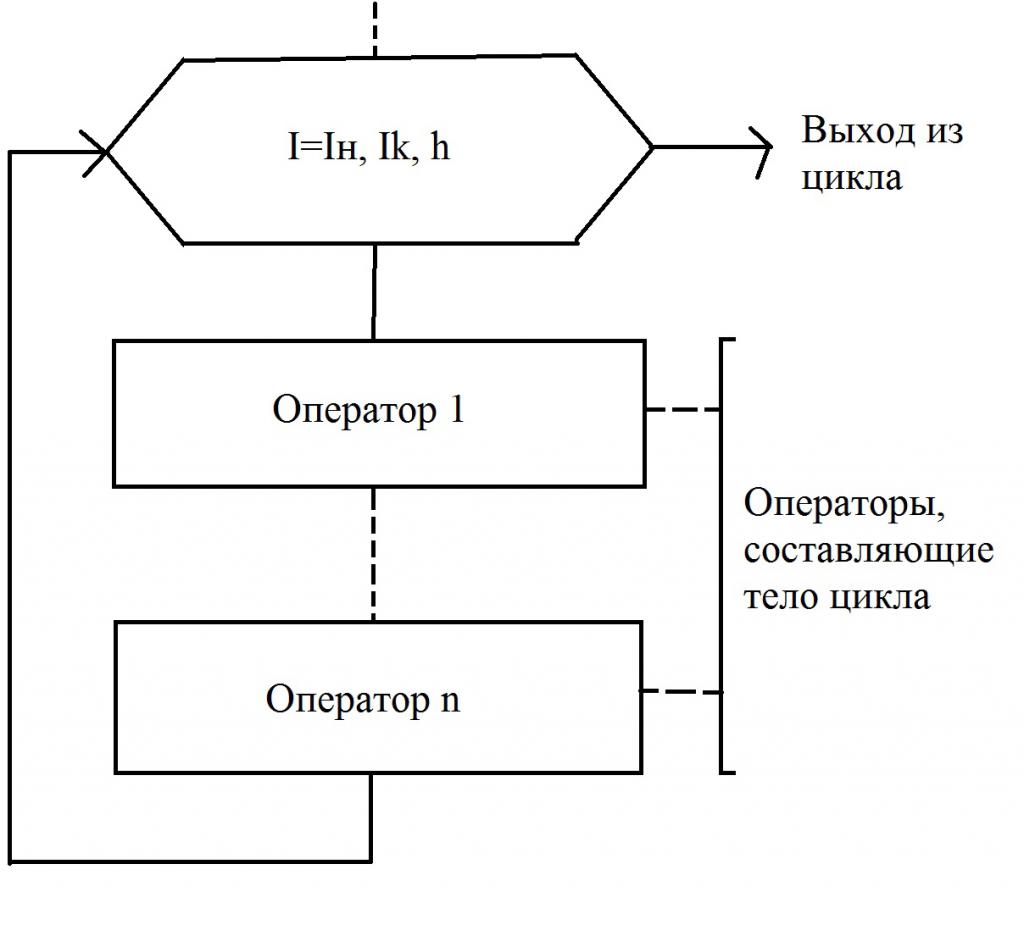
Циклы со счетчиками
На рисунке изображена простая блок-схема, в которой имеется цикл со счетчиком. Такой тип алгоритмов показывает, что заранее известно количество повторений данного цикла. И это число фиксировано. При этом переменная, считающая число шагов (повторений), так и называется – счетчик. Иногда в учебниках можно встретить иные определения – параметр цикла, управляющая переменная.
Блок-схема очень наглядно иллюстрирует, как работает цикл со счетчиком. Прежде чем приступить к выполнению первого шага, нужно присвоить начальное значение счетчику – это может быть любое число, оно зависит от конкретного алгоритма. В том случае, когда конечное значение меньше величины счетчика, начнет выполняться определенная группа команд, которые составляют тело цикла.
После того, как тело будет выполнено, счетчик меняется на величину шага счетчика, обозначенную буквой h. В том случае, если значение, которое получится, будет меньше конечного, цикл будет продолжаться. И закончится он лишь в тогда, когда конечное значение будет меньше, чем счетчик цикла. Только в этом случае произойдет выполнение того действия, которое следует за циклом.
Обычно в обозначениях блок-схем используется блок, который называется «Подготовка». В нем прописывается счетчик, а затем указываются такие данные: начальное и конечное значения, шаг изменения. На блок-схеме это параметры I н, Ik и h, соответственно. В том случае, когда h=1, величину шага не записывают. В остальных случаях делать это обязательно. Необходимо придерживаться простого правила – линия потока должна входить сверху. А линия потока, которая выходит снизу (или справа, в зависимости от конкретного алгоритма), должна показывать переход к последующему оператору.
Теперь вы полностью изучили описание блок-схемы, изображенной на рисунке. Можно перейти к дальнейшему изучению. Когда используется цикл со счетчиком, требуется соблюдать определенные условия:
- В теле не разрешается изменять (принудительно) значение счетчика.
- Запрещено передавать управление извне оператору тела. Другими словами, войти в цикл можно только из его начала.
Видео:Циклические алгоритмыСкачать

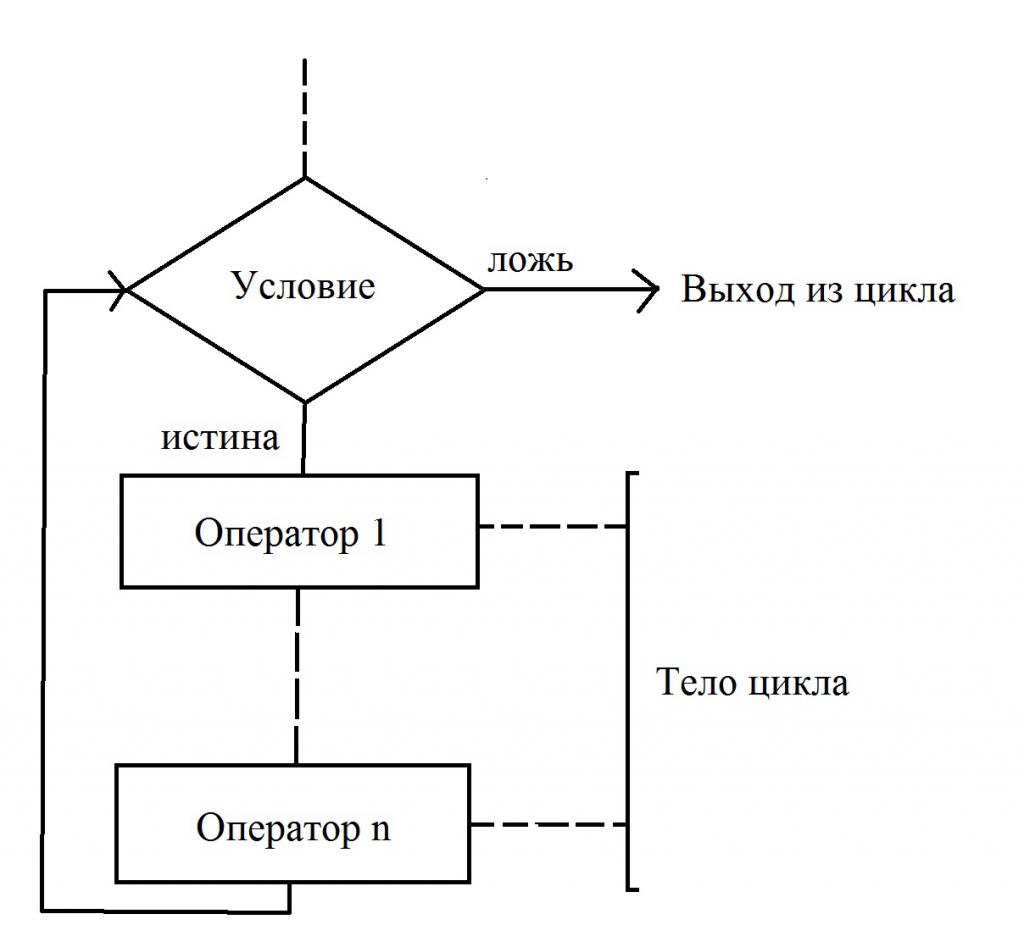
Циклы с предусловием
Этот тип циклов применяется в тех случаях, когда количество повторений заранее неизвестно. Цикл с предусловием – это тип алгоритма, в котором непосредственно перед началом выполнения тела осуществляется проверка условия, при котором допускается переход к следующему действию. Обратите внимание на то, как изображаются элементы блок-схемы.
В том случае, когда условие выполняется (утверждение истинно), происходит переход к началу тела цикла. Непосредственно в нем изменяется значение хотя бы одной переменной, влияющей на значение поставленного условия. Если не придерживаться этого правила, получим «зацикливание». В том случае, если после следующей проверки условия выполнения тела цикла оказывается, что оно ложное, то происходит выход.
В блок-схемах алгоритмов допускается осуществлять проверку не истинности, а ложности начального условия. При этом из цикла произойдет выход только в том случае, если значение условия окажется истинным. Оба варианта правильные, их использование зависит от того, какой конкретно удобнее использовать для решения той или иной задачи. Такой тип цикла имеет одну особенность – тело может не выполниться в случае, когда условие ложно или истинно (в зависимости от варианта, который применяется для решения алгоритма).
Ниже приведена блок-схема, которая описывает все эти действия:
Видео:Программа FBD для PLC на запуск двигателя звезда-треугольникСкачать

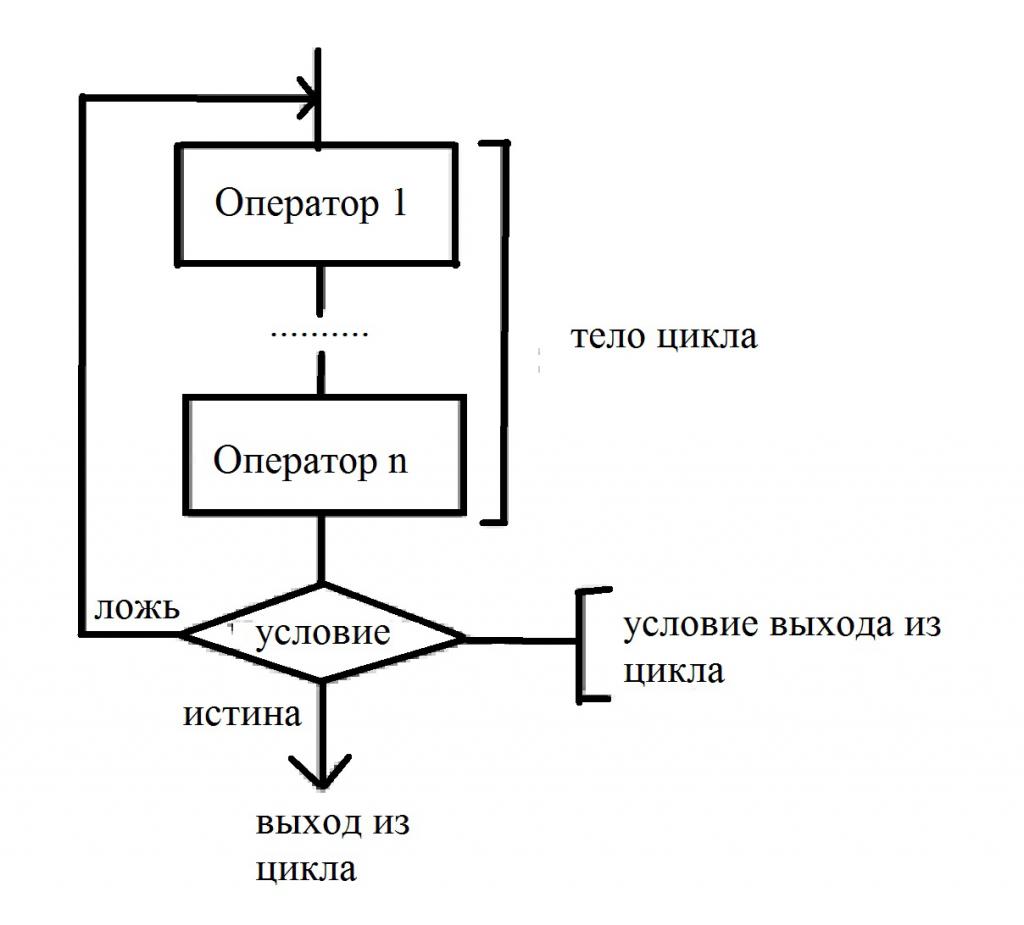
Что такое цикл с постусловием?
Если внимательно присмотреться, то этот вид циклов чем-то похож на предыдущий. Самостоятельно построить блок-схему, описывающую этот цикл, мы сейчас и попробуем. Особенность заключается в том, что неизвестно заранее число повторений. А условие задается уже после того, как произошел выход из тела. Отсюда видно, что тело, независимо от решения, будет выполняться как минимум один раз. Для наглядности взгляните на блок-схему, описывающую выполнение условия и операторов:
Ничего сложного в построении алгоритмов с циклами нет, достаточно в них только один раз разобраться. А теперь перейдем к более сложным конструкциям.
Видео:Этому не учат, а стоило бы. Чем отличается звезда от треугольника? #звезда #треугольник #двигательСкачать

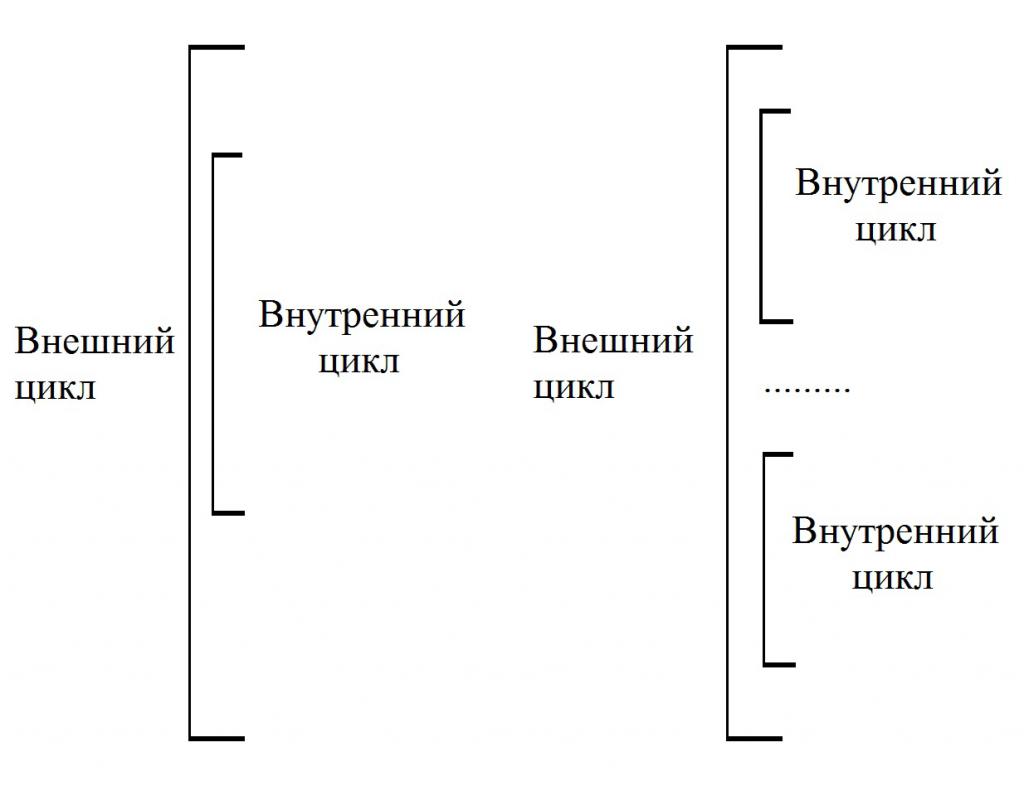
Сложные циклы
Сложные – это такие конструкции, внутри которых есть один или больше простых циклов. Иногда их называют вложенными. При этом те конструкции, которые охватывают иные циклы, называют «внешними». А те, которые входят в конструкцию внешних – внутренними. При выполнении каждого шага внешнего цикла происходит полная прокрутка внутреннего, как представлено на рисунке:
Вот и все, вы рассмотрели основные особенности построения блок-схем для решения алгоритмов, знаете принципы и правила. Теперь можно рассмотреть конкретные примеры блок-схем из жизни. Например, в психологии такие конструкции используются для того, чтобы человек решил какой-то вопрос:
Или пример из биологии для решения поставленной задачи:
Видео:U PERM | PLL | треугольник рёберСкачать

Решение задач с блок-схемами
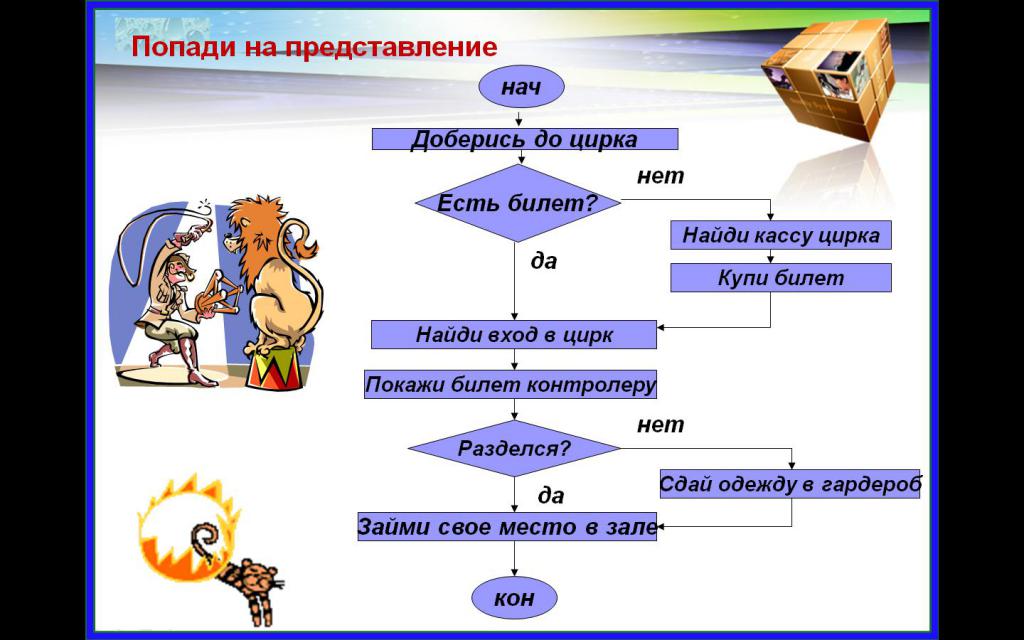
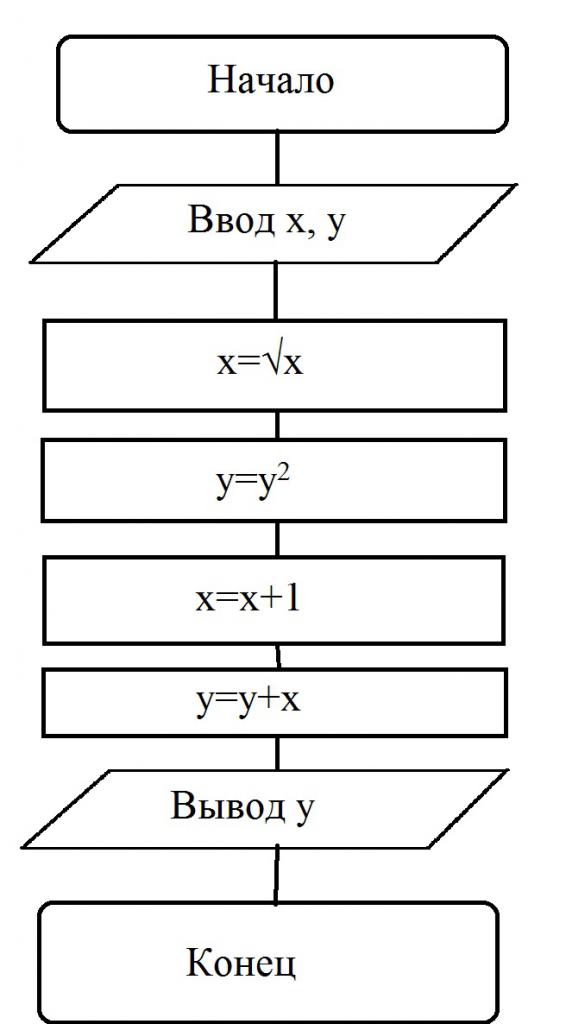
А теперь рассмотрим примеры задач с блок-схемами, которые могут попасться в учебниках информатики. Например, задана блок-схема, по которой решается какой-то алгоритм:
При этом пользователь самостоятельно вводит значения переменных. Допустим, х=16, а у=2. Процесс выполнения такой:
- Производится ввод значений х и у.
- Выполняется операция преобразования: х=√16=4.
- Выполняется условие: у=у 2 =4.
- Производится вычисление: х=(х+1)=(4+1)=5.
- Дальше вычисляется следующая переменная: у=(у+х)=(5+4)=9.
- Выводится решение: у=9.
На этом примере блок-схемы по информатике хорошо видно, как происходит решение алгоритма. Нужно обратить внимание на то, что значения х и у задаются на начальном этапе и они могут быть любыми.
Видео:Кубик рубика 2х2 одной рукой. Сборка на чемпионате в Челябинске 22 октября 2022 г. URAL AUTUMNСкачать

Треугольник Паскаля — формула, свойства и применение
Видео:Математика это не ИсламСкачать

Основная формула
Строки треугольника обычно нумеруются, начиная со строки n = 0 в верхней части. Записи в каждой строке целочисленные и нумеруются слева, начиная с k = 0, обычно располагаются в шахматном порядке относительно чисел в соседних строчках. Построить фигуру можно следующим образом:
- В центре верхней части листа ставится цифра «1».
- В следующем ряду — две единицы слева и справа от центра (получается треугольная форма).
- В каждой последующей строке ряд будет начинаться и заканчиваться числом «1». Внутренние члены вычисляются путём суммирования двух цифр над ним.
Запись в n строке и k столбце паскалевской фигуры обозначается (n k). Например, уникальная ненулевая запись в самой верхней строке (0 0) = 1. С помощью этого конструкция предыдущего абзаца может быть записана следующим образом, образуя формулу треугольника Паскаля (n k) = (n — 1 k-1) + (n — 1 k), для любого неотрицательного целого числа n и любого целого числа k от 0 до n включительно. Трёхмерная версия называется пирамидой или тетраэдром, а общие — симплексами.
Видео:Что скрывает фрактальный треугольник? // Vital MathСкачать

История открытия
Паскаль ввёл в действие многие ранее недостаточно проверенные способы использования чисел треугольника, и он подробно описал их в, пожалуй, самом раннем из известных математических трактатов, специально посвящённых этому вопросу, в труде об арифметике Traité du triangle (1665). За столетия до того обсуждение чисел возникло в контексте индийских исследований комбинаторики и биномиальных чисел, а у греков были работы по «фигурным числам».
Из более поздних источников видно, что биномиальные коэффициенты и аддитивная формула для их генерации были известны ещё до II века до нашей эры по работам Пингала. К сожалению, бо́льшая часть трудов была утеряна. Варахамихира около 505 года дал чёткое описание аддитивной формулы, а более подробное объяснение того же правила было дано Халаюдхой (около 975 года). Он также объяснил неясные ссылки на Меру-прастаара, лестницы у горы Меру, дав первое сохранившееся определение расположению этих чисел, представленных в виде треугольника.
Примерно в 850 году джайнский математик Махавира вывел другую формулу для биномиальных коэффициентов, используя умножение, эквивалентное современной формуле. В 1068 году Бхаттотпала во время своей исследовательской деятельности вычислил четыре столбца первых шестнадцати строк. Он был первым признанным математиком, который уравнял аддитивные и мультипликативные формулы для этих чисел.
Примерно в то же время персидский учёный Аль-Караджи (953–1029) написал книгу (на данный момент утраченную), в которой содержалось первое описание треугольника Паскаля. Позднее работа была переписана персидским поэтом, астрономом и математиком Омаром Хайямом (1048–1131). Таким образом, в Иране фигура упоминается как треугольник Хайяма.
Известно несколько теорем, связанных с этой темой, включая биномы. Хайям использовал метод нахождения n-x корней, основанный на биномиальном разложении и, следовательно, на одноимённых коэффициентах. Треугольник был известен в Китае в начале XI века благодаря работе китайского математика Цзя Сианя (1010–1070). В XIII веке Ян Хуэй (1238–1298) представил этот способ, и поэтому в Китае он до сих пор называется треугольником Ян Хуэя.
На западе биномиальные коэффициенты были рассчитаны Жерсонидом в начале XIV века, он использовал мультипликативную формулу. Петрус Апиан (1495–1552) опубликовал полный треугольник на обложке своей книги примерно в 1527 году. Это была первая печатная версия фигуры в Европе. Майкл Стифель представил эту тему как таблицу фигурных тел в 1544 году.
В Италии паскалевский треугольник зовут другим именем, в честь итальянского алгебраиста Никколо Фонтана Тарталья (1500–1577). Вообще, современное имя фигура приобрела благодаря Пьеру Раймонду до Монтрмору (1708), который назвал треугольник «Таблица Паскаля для сочетаний» (дословно: Таблица мистера Паскаля для комбинаций) и Абрахамом Муавром (1730).
Видео:Мастер Пираморфикс / Самый Сложный Кубик РубикаСкачать

Отличительные черты
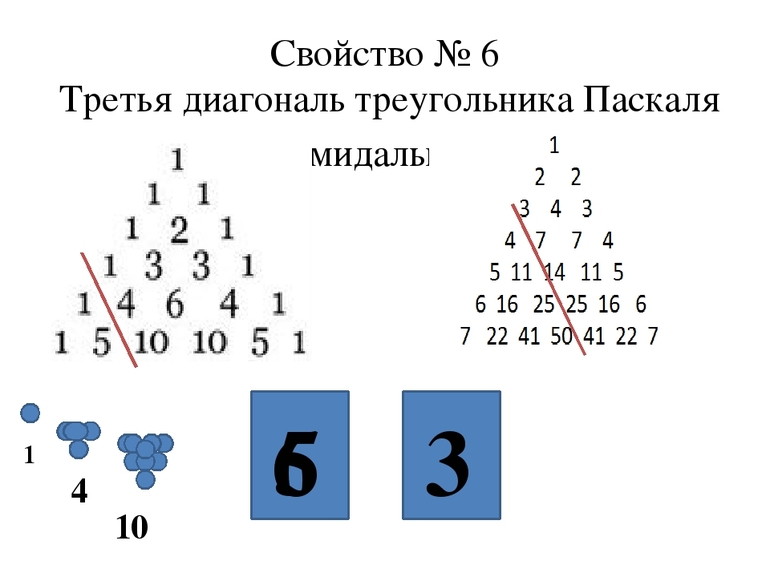
Треугольник Паскаля и его свойства — тема довольно обширная. Главное, в нём содержится множество моделей чисел. Обзор следует начать с простого — ряды:
- Сумма элементов одной строки в два раза больше суммы строки, предшествующей ей. Например, строка 0 (самая верхняя) имеет значение 1, строчка 1–2, а 2 имеет значение 4 и т. д. Это потому что каждый элемент в строке производит два элемента в следующем ряду: один слева и один справа. Сумма элементов строки n равна 2 n .
- Принимая произведение элементов в каждой строке, последовательность продуктов можно связать с основанием натурального логарифма.
- В треугольнике Паскаля через бесконечный ряд Нилаканты можно найти число Пи.
- Значение строки, если каждая запись считается десятичным знаком (имеется в виду, что числа больше 9 переносятся соответственно), является степенью 11 (11 n для строки n). Таким образом, в строке 2 ⟨1, 2, 1⟩ становится 11 2 , равно как ⟨1, 5, 10, 10, 5, 1⟩ в строке пять становится (после переноса) 161, 051, что составляет 11 5 . Это свойство объясняется установкой x = 10 в биномиальном разложении (x + 1) n и корректировкой значений в десятичной системе.
- Некоторые числа в треугольнике Паскаля соотносятся с числами в треугольнике Лозанича.
- Сумма квадратов элементов строки n равна среднему элементу строки 2 n. Например, 1 2 + 4 2 + 6 2 + 4 2 + 1 2 = 70.
- В любой строчке n, где n является чётным, средний член за вычетом члена в двух точках слева равен каталонскому числу (n / 2 + 1).
- В строчке р, где р представляет собой простое число, все члены в этой строке, за исключением 1s, являются кратными р.
- Чётность. Для измерения нечётных терминов в строке n необходимо преобразовать n в двоичную форму. Пусть x будет числом 1s в двоичном представлении. Тогда количество нечётных членов будет 2 х . Эти числа являются значениями в последовательности Гулда.
- Каждая запись в строке 2 n -1, n ≥ 0, является нечётной.
- Полярность. Когда элементы строки треугольника Паскаля складываются и вычитаются вместе последовательно, каждая строка со средним числом, означающим строки с нечётным числом целых чисел, даёт 0 в качестве результата.
Диагонали треугольника содержат фигурные числа симплексов. Например:
- Идущие вдоль левого и правого краёв диагонали содержат только 1.
- Рядом с рёбрами диагонали содержат натуральные числа по порядку.
- Двигаясь внутрь, следующая пара содержит треугольные числа по порядку.
- Следующая пара — тетраэдрические, а следующая пара — числа пятиугольника.
Существуют простые алгоритмы для вычисления всех элементов в строке или диагонали без вычисления других элементов или факториалов.
Общие свойства
Образец, полученный путём раскраски только нечётных чисел, очень похож на фрактал, называемый треугольником Серпинского. Это сходство становится всё более точным, так как рассматривается больше строк в пределе, когда число рядов приближается к бесконечности, получающийся в результате шаблон представляет собой фигуру, предполагающую фиксированный периметр. В целом числа могут быть окрашены по-разному в зависимости от того, являются ли они кратными 3, 4 и т. д.
В треугольной части сетки количество кратчайших путей от заданного до верхнего угла треугольника является соответствующей записью в паскалевском треугольнике. На треугольной игровой доске Плинко это распределение должно давать вероятности выигрыша различных призов. Если строки треугольника выровнены по левому краю, диагональные полосы суммируются с числами Фибоначчи.
Благодаря простому построению факториалами можно дать очень простое представление фигуры Паскаля в терминах экспоненциальной матрицы: треугольник — это экспонента матрицы, которая имеет последовательность 1, 2, 3, 4… на её субдиагонали, а все другие точки — 0.
Количество элементов симплексов фигуры можно использовать в качестве справочной таблицы для количества элементов (рёбра и углы) в многогранниках (треугольник, тетраэдр, квадрат и куб).
Шаблон, созданный элементарным клеточным автоматом с использованием правила 60, является в точности паскалевским треугольником с биномиальными коэффициентами, приведёнными по модулю 2. Правило 102 также создаёт этот шаблон, когда завершающие нули опущены. Правило 90 создаёт тот же шаблон, но с пустой ячейкой, разделяющей каждую запись в строках. Фигура может быть расширена до отрицательных номеров строк.
Секреты треугольника
Конечно, сейчас большинство расчётов для решения задач не в классе можно сделать с помощью онлайн-калькулятора. Как пользоваться треугольником Паскаля и для чего он нужен, обычно рассказывают в школьном курсе математики. Однако его применение может быть гораздо шире, чем принято думать.
Начать следует со скрытых последовательностей. Первые два столбца фигуры не слишком интересны — это только цифры и натуральные числа. Следующий столбец — треугольные числа. Можно думать о них, как о серии точек, необходимых для создания групп треугольников разных размеров.
Точно так же четвёртый столбец — это тетраэдрические числа или треугольные пирамидальные. Как следует из их названия, они представляют собой раскладку точек, необходимых для создания пирамид с треугольными основаниями.
Столбцы строят таким образом, чтобы описывать «симплексы», которые являются просто экстраполяциями идеи тетраэдра в произвольные измерения. Следующий столбец — это 5-симплексные числа, затем 6-симплексные числа и так далее.
Полномочия двойки
Если суммировать каждую строку, получатся степени основания 2 начиная с 2⁰ = 1. Если изобразить это в таблице, то получится следующее:
| 1 | ||||||||||||||
| 1 | + | 1 | = | 2 | ||||||||||
| 1 | + | 2 | + | 1 | = | 4 | ||||||||
| 1 | + | 3 | + | 3 | + | 1 | = | 8 | ||||||
| 1 | + | 4 | + | 6 | + | 4 | + | 1 | = | 16 | ||||
| 1 | + | 5 | + | 10 | + | 10 | + | 5 | + | 1 | = | 32 | ||
| 1 | + | 6 | + | 15 | + | 20 | + | 15 | + | 6 | + | 1 | = | 64 |
Суммирование строк показывает силы базы 2.
Силы одиннадцати
Треугольник также показывает силы основания 11. Всё, что нужно сделать, это сложить числа в каждом ряду вместе. Как показывает исследовательский опыт, этого достаточно только для первых пяти строк. Сложности начинаются, когда записи состоят из двузначных чисел. Например:
| 1 | = | 11° |
| 11 | = | 11¹ |
| 121 | = | 11² |
| 1331 | = | 11³ |
Оказывается, всё, что нужно сделать — перенести десятки на одно число слева.
Совершенные квадраты
Если утверждать, что 4² — это 6 + 10 = 16, то можно найти идеальные квадраты натуральных чисел в столбце 2, суммируя число справа с числом ниже. Например:
- 2² → 1 + 3 = 4
- 3² → 3 + 6
- 4² → 6 + 10 = 16 и так далее.
Комбинаторные варианты
Чтобы раскрыть скрытую последовательность Фибоначчи, которая на первый взгляд может отсутствовать, нужно суммировать диагонали лево-выровненного паскалевского треугольника. Первые 7 чисел в последовательности Фибоначчи: 1, 1, 2, 3, 5, 8, 13… найдены. Используя исходную ориентацию, следует заштриховать все нечётные числа, и получится изображение, похожее на знаменитый фрактальный треугольник Серпинского.
Возможно, самое интересное соотношение, найденное в треугольнике — это то, как можно использовать его для поиска комбинаторных чисел, поскольку его первые шесть строк написаны с помощью комбинаторной записи. Поэтому, если нужно рассчитать 4, стоит выбрать 2, затем максимально внимательно посмотреть на пятую строку, третью запись (поскольку счёт с нуля), и будет найден ответ.
Действия с биномами
Например, есть бином (x + y), и стоит задача повысить его до степени, такой как 2 или 3. Обычно нужно пройти долгий процесс умножения (x + y)² = (x + y)(x + y) и т. д. Если воспользоваться треугольником, решение будет найдено гораздо быстрее. К примеру, нужно расширить (x + y)³. Поскольку следует повышать (x + y) до третьей степени, то необходимо использовать значения в четвёртом ряду фигуры Паскаля (в качестве коэффициентов расширения). Затем заполнить значения x и y. Получится следующее: 1 x³ + 3 x²y + 3 xy² + 1 y³. Степень каждого члена соответствует степени, до которой возводится (x + y).
В виде более удобной формулы этот процесс представлен в теореме бинома. Как известно, всё лучше разбирать на примерах. Итак — (2x – 3)³. Пусть x будет первым слагаемым, а y — вторым. Тогда x = 2x, y = –3, n = 3 и k — целые числа от 0 до n = 3, в этом случае k = . Следует внести эти значения в формулу. Затем заполнить значения для k, которое имеет 4 разные версии, их нужно сложить вместе. Лучше упростить условия с показателями от нуля до единицы.
Как известно, комбинаторные числа взяты из треугольника, поэтому можно просто найти четвёртую строку и подставить в значения 1, 3, 3, 1 соответственно, используя соответствующие цифры Паскаля 1, 3, 3, 1. Последнее — необходимо завершить умножение и упрощение, в итоге должно получиться: 8 x³ — 36 x² + 54x — 27. С помощью этой теоремы можно расширить любой бином до любой степени, не тратя время на умножение.
Биномиальное распределение описывает распределение вероятностей на основе экспериментов, которые можно разделить на группы с двумя возможными исходами. Самый классический пример этого — бросание монеты. Например, есть задача выбросить «решку» — успех с вероятностью p. Тогда выпадение «орла» является случаем «неудачи» и имеет вероятность дополнения 1 – p.
Если спроектировать этот эксперимент с тремя испытаниями, с условием, что нужно узнать вероятность выпадения «решки», можно использовать функцию вероятности массы (pmf) для биномиального распределения, где n — это количество испытаний, а k — это число успехов. Предполагаемая вероятность удачи — 0,5 (р = 0,5). Самое время обратиться к треугольнику, используя комбинаторные числа: 1, 3, 3, 1. Вероятность получить ноль или три «решки» составляет 12,5%, в то время как переворот монеты один или два раза на сторону «орла» — 37,5%. Вот так математика может применяться в жизни.