- Параллельные прямые
- Признак параллельности прямых
- Параллельные прямая и плоскость
- Признак параллельности прямой и плоскости
- Свойство прямой, параллельной данной плоскости
- Параллельные плоскости
- Признаки параллельности плоскостей
- Свойства параллельных плоскостей
- Параллельность и перпендикулярность прямых и плоскостей в пространстве
- Геометрия. 10 класс
- 🎦 Видео
Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Параллельные прямые
Параллельные прямые – прямые, которые лежат в одной плоскости и не пересекаются.
Признак параллельности прямых
Две прямые, параллельные третьей, параллельны между собой.
Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельные прямая и плоскость
Прямая и плоскость называются параллельными , если они не имеют общих точек.
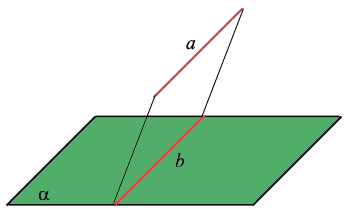
Признак параллельности прямой и плоскости
Если прямая, не принадлежащая данной плоскости, параллельна какой-нибудь прямой этой плоскости, то она параллельна этой плоскости.
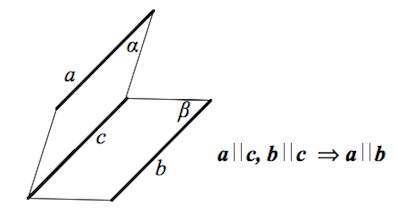
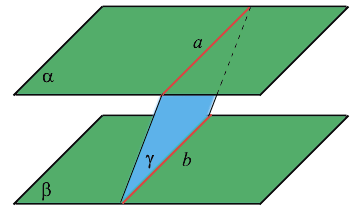
Свойство прямой, параллельной данной плоскости
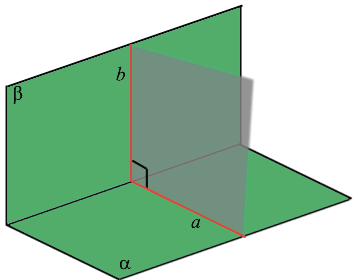
Если плоскость β проходит через прямую a , параллельную плоскости α , и пересекает эту плоскость по прямой b , то b || a .
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Параллельные плоскости
Параллельные плоскости – плоскости, которые не пересекаются.
Признаки параллельности плоскостей
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.
Если каждая из двух данных плоскостей параллельна третьей плоскости, то данные две плоскости параллельны между собой.
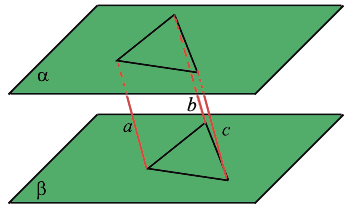
Свойства параллельных плоскостей
Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны.
Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Видео:Параллельность прямой к плоскостиСкачать

Параллельность и перпендикулярность прямых и плоскостей в пространстве
Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости называются скрещивающимися. Прямая и плоскость в пространстве называются параллельными, если они не пересекаются.
Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.
Две плоскости называются параллельными, если они не пересекаются.
Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны. Через точку, не лежащую в данной плоскости, можно провести параллельную плоскость, и притом только одну.

Отрезки параллельных прямых между параллельными плоскостями равны.

Прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой в плоскости, проходящей через точку их пересечения.
Прямая, пересекающая плоскость, перпендикулярна плоскости, если она перпендикулярна двум прямым в плоскости, проходящим через точку их пересечения.
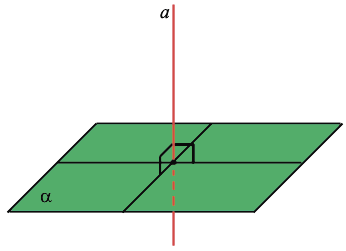
Через каждую точку плоскости можно провести перпендикулярную ей прямую, и только одну. Все прямые, перпендикулярные данной плоскости, параллельны.
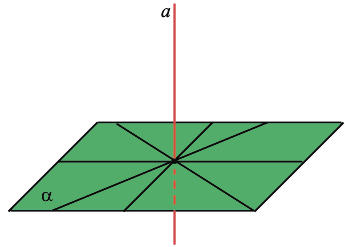
Перпендикуляр, опущенный из данной точки на данную плоскость, — это отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, которая перпендикулярна плоскости. Основание перпендикуляра — это его конец, лежащий в плоскости.
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного от этой точки на плоскость.
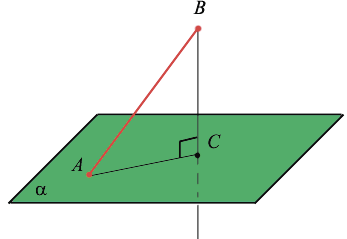
Наклонная, проведенная из данной точки к данной плоскости, — это любой отрезок, соединяющий данную точку с точкой плоскости, который не является перпендикуляром к плоскости. Конец отрезка, который лежит в плоскости, — это основание наклонной. Проекция наклонной — это отрезок, который соединяет основания перпендикуляра (точку С) и наклонной (точку А).
Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной. И обратно, если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
Две пересекающиеся плоскости называются перпендикулярными, если плоскость, перпендикулярная прямой их пересечения, пересекает данные плоскости по перпендикулярным прямым.
Так как 
Поделись с друзьями в социальных сетях:
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок №4. Параллельность прямых, прямой и плоскости
Перечень вопросов, рассматриваемых в теме
- Определение параллельных прямых;
- Теорема о единственности прямой, параллельной данной, проходящей через данную точку;
- лемма о двух параллельных прямых;
- теорему о параллельности трех прямых;
- определение параллельных прямой и плоскости;
- признаком параллельности прямой и плоскости.
Глоссарий по теме
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые − прямые, которые не лежат в одной плоскости.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл.– М.: Просвещение, 2014. 255 с.
Зив Б. Г. Дидактические материалы. Геометрия 10 кл. – М.: Просвещение, 2014. 96 с.
Глазков Ю. А., Юдина И. И., Бутузов В.Ф. Рабочая тетрадь. Геометрия 10 кл.-М.: Просвещение, 2013. 65 с.
Теоретический материал для самостоятельного изучения
Геометрия, которую мы изучаем, называется евклидовой, по имени древнегреческого ученого Евклида (3 век до нашей эры), который создал целый труд по математике под названием «Начала». В данной книге есть раздел о параллельных прямых.
В советском энциклопедическом словаре слово «параллельность» переводится с греческого языка, как «идущий рядом».
В средние века параллельность обозначалась знаком «=». В 1557 году Р. Рекордом для обозначения равенства был введен знак «=», которым мы пользуемся сейчас, а параллельность стали обозначать «║».
В книге «Начала» определение параллельных прямых звучало так «прямые, лежащие в одной плоскости и будучи бесконечно продолжены в обе стороны, ни с той, ни с другой стороны не пересекаются». Это определение почти не отличается от современного.
В области параллельных прямых работало очень много учёных: Н.И. Лобаческий (18-19 век); Аббас ал-Джаухари (работал в Багдаде в 9 веке); Фадл ал-Найризи (Богдад 10 век); Герард (Италия 12 век); Иоганн Генрих Ламберт (Берлин) и многие другие.
Каково расположение 2-х прямых на плоскости (совпадают, пересекаются, параллельны) (рис. 1 а, б, в).

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Давайте укажем некоторые пары параллельных прямых:
AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.
А теперь рассмотрим некоторые пары скрещивающихся прямых, как мы отметили, они не должны лежать в одной плоскости:
AB A₁D₁; AB B₁C₁; CD A₁D₁; CD B₁C₁; BC C₁D₁; BC A₁B₁; AB B₁C₁; AB A₁D₁.
Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
- М и а задают плоскость α
- Прямая, проходящая через точку М параллельно прямой а, должна лежать в одной плоскости с точкой М и прямой а, т.е. в плоскости α.
- В плоскости α через точку М проходит прямая, параллельная прямой а, и притом только одна- это нам известно из кураса планиметрии.
- На чертеже эта прямая обозначена буквой b .
- Следовательно, b-единственная прямая, проходящая через точку М паралельно прямой а.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Аналогично определяется праралельность отрезка и прямой, а так же паралельность двух лучей.

- Рассмотрим две параллельные прямые a и b и допустим, что прямая b пересекает плоскость α в точке M(а рис.).
- Мы знаем, что через параллельные прямые a и b можно провести только одну плоскость β. (теорема)
- Так как точка M находится на прямой b, то M также принадлежит плоскости β (б рис.). Если у плоскостей α и β есть общая точка M, то у этих плоскостей есть общая прямая p, которая является прямой пересечения этих плоскостей (4 аксиома).
- Прямые a, b и c находятся в плоскости β.
Если в этой плоскости одна из параллельных прямых b пересекает прямую p, то вторая прямая a тоже пересекает p.
- Точку пересечения прямых a и p обозначим за N.
Так как точка N находится на прямой p, то N находится в плоскости α и является единственной общей точкой прямой a и плоскости α.
- Значит, прямая a пересекает плоскость α в точке N.
Нам известно из курса планиметрии, что если три прямые лежат в одной плоскости и две из них параллельны третьей, то эти две прямые параллельны. Похожее утверждение имеет место и для трех прямых в пространстве.
Теорема. Если две прямые параллельны третьей прямой, то они параллельны.

Выберем точку M на прямой b.
Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).
Возможны два случая:
1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.
Пусть прямая b пересекает плоскость α.
Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным. Значит, прямая b находится в плоскости α.
Теперь нужно доказать, что прямые a и b параллельны.
Пусть у прямых a и b есть общая точка L.
Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.
Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.
Если две точки прямой лежат в данной плоскости, то по аксиоме А₂ вся прямая лежит в этой плоскости. Из этого следует, что возможны три расположения прямой и плоскости:
|
|
|






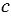









 . BC=AD= 8 см;
. BC=AD= 8 см;