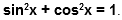Не табличные значения на окружности

В статье мы рассмотрим, как найти значения:

и других тригонометрических выражений без тригонометрической таблицы .

Для начала внимательно прочтите статью о числовой окружности . Вы должны научиться находить точки на окружности в числах с Пи .

Уже умеете? Тогда два ключевых утверждения:

— косинус числа равен абсциссе точки на числовой окружности
— синус числа равен ординате точки на числовой окружности

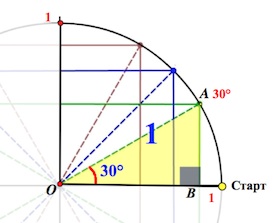
Например, пусть нам нужно найти синус и косинус числа (frac). Обозначим на числовой окружности точку со значением (frac).

Если построить все точно и крупно, то можно убедиться, что абсцисса этой точки будет равна (0,866…) , что соответствует числу (frac<sqrt>) , а ордината равна (0,5), то есть (frac).

Аналогично и для любой другой точки: значение абсциссы совпадает со значением косинуса, а ординаты – синуса. Поэтому:

В тригонометрии ось абсцисс часто называют «ось косинусов», а ординат – «ось синусов».

И обычно на них не наносят значения в десятичных ((0,1); (0,2); (0,3) и т.д.), а сразу отмечают стандартные значения для синуса и косинуса: (frac =0,5); (frac<sqrt> ≈0,707); (frac<sqrt>≈0,866), причем, как со знаком плюс, так и минус. Почему стандартные значения синуса и косинуса именно (frac),(frac<sqrt>) и (frac<sqrt>) вы можете узнать из этого видео .

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Как находить значения синуса и косинуса без таблицы, а только с помощью круга?

1. Начертите круг и оси косинусов и синусов.
2. Отметьте на круге число, синус и косинус которого надо найти. Если с этим возникают проблемы, прочитайте здесь о том, как расставлять числа на числовой окружности.
3. Найдите координаты точки, используя картинку ниже.

Пример. Найдите синус и косинус для числа (-frac).
Решение:(-frac=-frac-frac=-π-frac) , то есть, чтобы отметить на окружности точку (-frac) сначала находим число (-π) и от него в отрицательную сторону откладываем дугу длиной (frac).

Отмечаем число, синус и косинус которого надо найти:

Точка (frac) совпадает с (1) на оси синусов, значит (sin⁡frac=1). А если провести перпендикуляр из точки (frac) до оси косинусов, то можно убедиться, что он попадет в (0). Поэтому (cosfrac=0).

И тут некоторые из вас подумали: «с кругом, на котором подписаны числа, каждый дурак сможет посчитать, а что делать, когда его под рукой нет? Что делать на ЕГЭ?» Ответ прост – нарисуйте круг сами! Для этого вам будет нужно понять логику расположения чисел на осях (подробнее об этом читайте в статье « Как запомнить тригонометрический кру г »).

Пример. Найдите а) (sin⁡frac), б) (cos⁡frac), в) (sin⁡(-frac)) .
Решение: а) Чертим круг, оси и отмечаем число (frac). Обращаем внимание на ось синусов и понимаем, что точка совпала с (-1), получается (sin⁡frac=-1).
б) (frac=frac-frac=π-frac) — отмечаем число на круге. Проводим перпендикуляр до оси косинусов и вспоминаем, что точки со знаменателем (4) находятся посередине. Мы еще попали и в отрицательную часть оси косинусов, получается (cos⁡frac=-frac<sqrt>).
в) (-frac) – отмечаем число на круге. Видим, что перпендикуляр к оси синусов попал в точку близкую к (-1), значит (sin⁡(-frac)=-frac<sqrt>).

Как видите не обязательно рисовать, очень красивую или очень большую окружность — вы можете определить нужное вам значение, быстро набросав круг. И ничего не надо учить!

Если вы хотите еще примеров с вычислением синусов и косинусов без тригонометрической таблицы, то прочтите эту статью.

Видео:Таблица значений тригонометрических функций - как её запомнить!!!Скачать

Единичная окружность

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Тригонометрическая окружность. Как выучить?Скачать

Единичная окружность в тригонометрии

Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.

Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.

Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.

Поясним, как единичная окружность связана с тригонометрией.

В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.

Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.

Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.

Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:

• Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
• Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
• В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
• В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.

Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:

Радиан — одна из мер для определения величины угла.

Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.

Число радиан для полной окружности — 360 градусов.

Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.

Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.

Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:

• 2π радиан = 360°
• 1 радиан = (360/2π) градусов
• 1 радиан = (180/π) градусов
• 360° = 2π радиан
• 1° = (2π/360) радиан
• 1° = (π/180) радиан

Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.

Уравнение единичной окружности

При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Видео:ЗНАЧЕНИЯ СИНУСА И КОСИНУСА НА ОКРУЖНОСТИСкачать

Тригонометрический круг. Основные значения тригонометрических функций

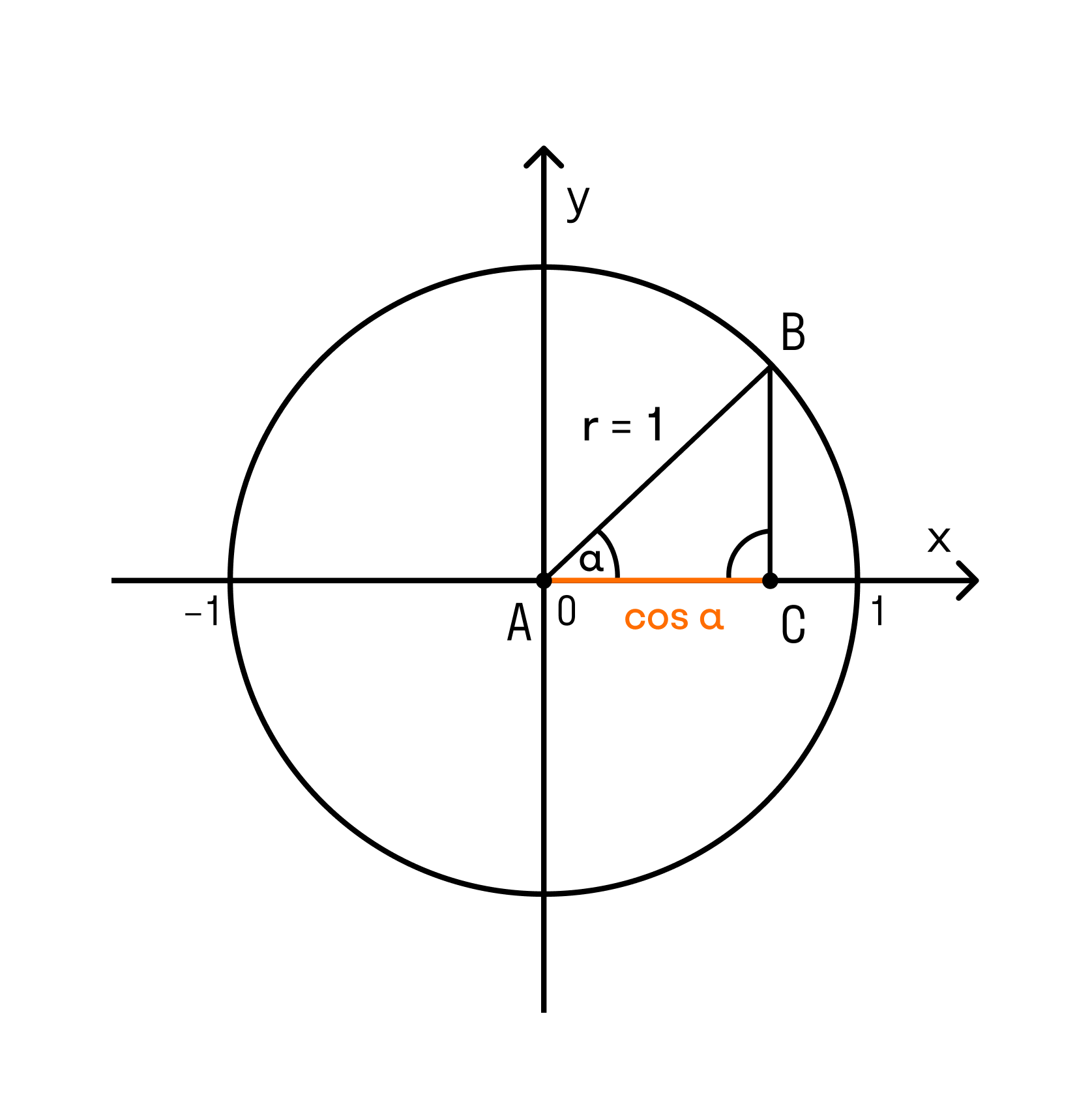
Если вы уже знакомы с тригонометрическим кругом , и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, тригонометрический круг :

Мы же здесь будем все подробно разбирать шаг за шагом + показать

Тригонометрический круг – не роскошь, а необходимость

Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…

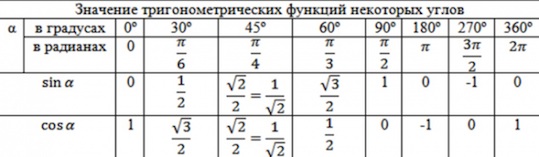
Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений.

Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!

Нас выручит тригонометрический круг ! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!

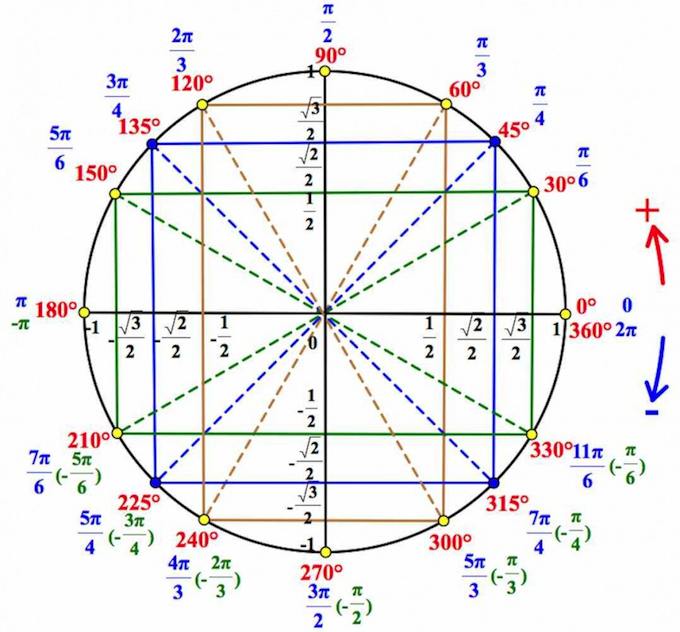
К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул , чему равен синус, скажем, градусов, или .

Никак. можно, конечно, подключить формулы приведения… А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!

А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.

Знакомство с тригонометрическим кругом

Давайте по порядку.

Сначала выпишем вот такой ряд чисел:

И, наконец, такой:

Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .

Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».

И зачем оно нам?

Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.

Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).

От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .

Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.

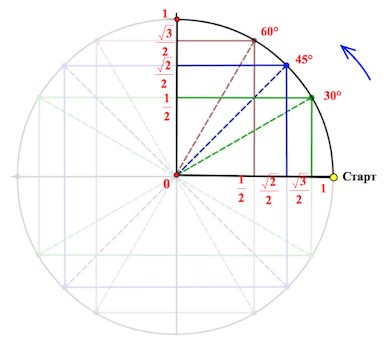
Это почему же, спросите вы?

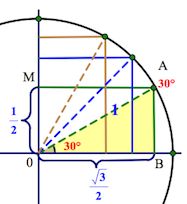
Не будем разбирать все. Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.

Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть ).

Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора

Надеюсь, уже что-то становится понятно?

Так вот точка В и будет соответствовать значению , а точка М – значению

Аналогично с остальными значениями первой четверти.

Как вы понимаете, привычная нам ось (ox) будет осью косинусов , а ось (oy) – осью синусов . Про тангенс и котангенс позже.

Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.

Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг , без которого никуда в тригонометрии.

А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье.

🌟 Видео

Как искать точки на тригонометрической окружности.Скачать

Отбор корней по окружностиСкачать

Как найти значения синуса и косинуса, НЕ запоминая!Скачать

10 класс, 11 урок, Числовая окружностьСкачать

Спидран: Как запомнить таблицу синусов и косинусов за 1 минуту? Евгений ДолжкевичСкачать

Тригонометрическая окружность для непонимающихСкачать

Как запомнить тригонометрический круг специально ничего не выучивая?Скачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Вычисление значений тригонометрических функцийСкачать

ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

СИНУС И КОСИНУС ЛЮБЫХ УГЛОВ | ТригонометрияСкачать

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

Значения тригонометрических функций на окружности.Скачать

🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать