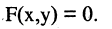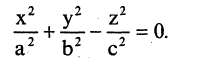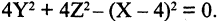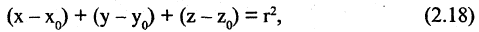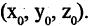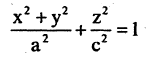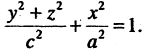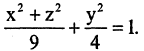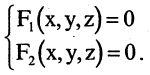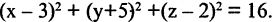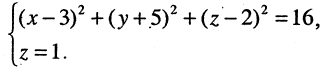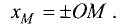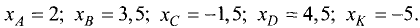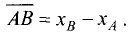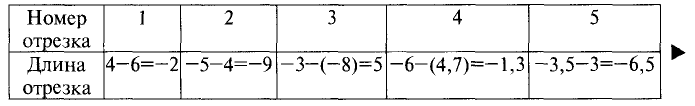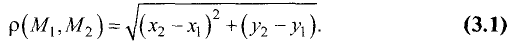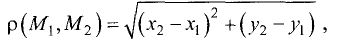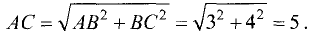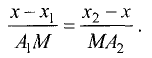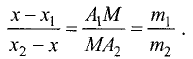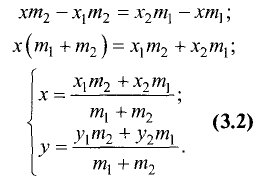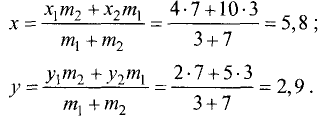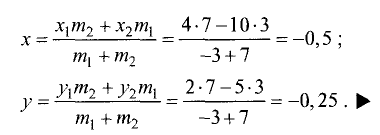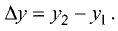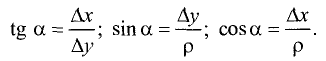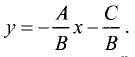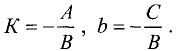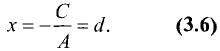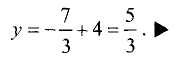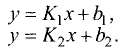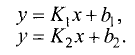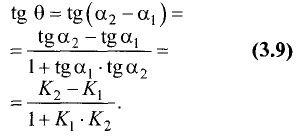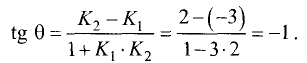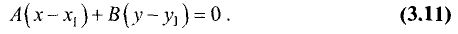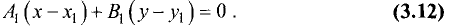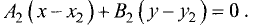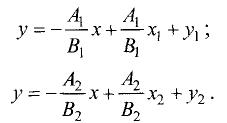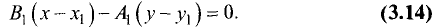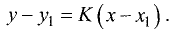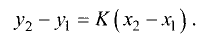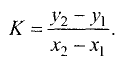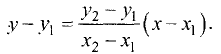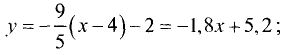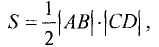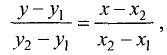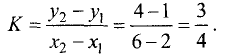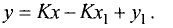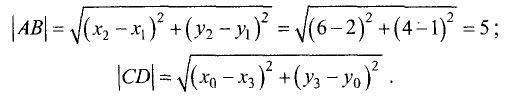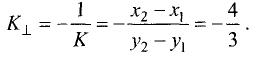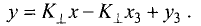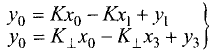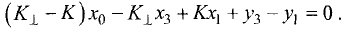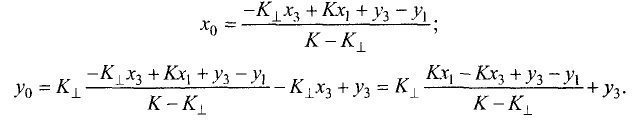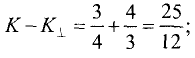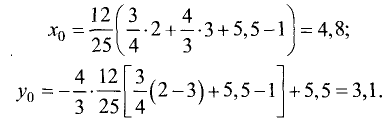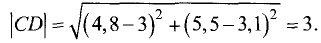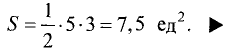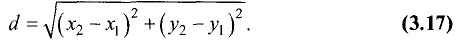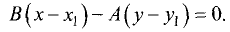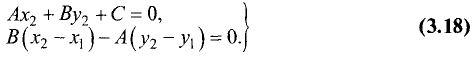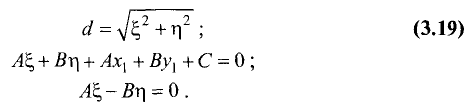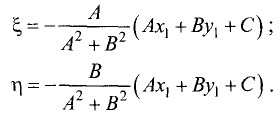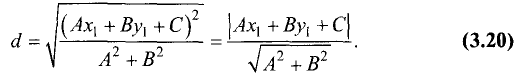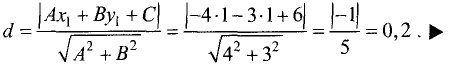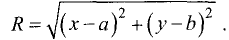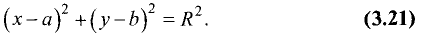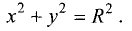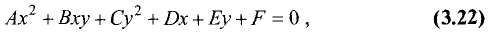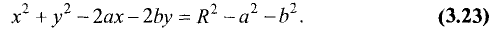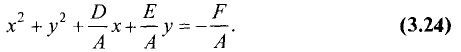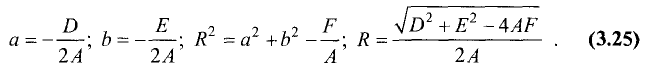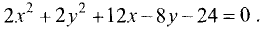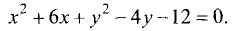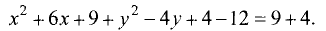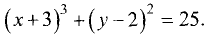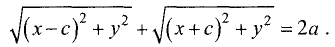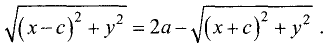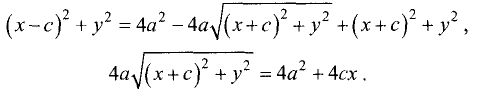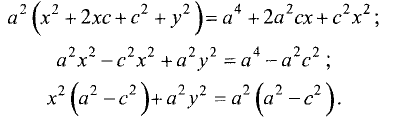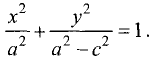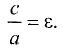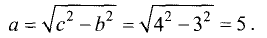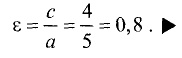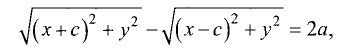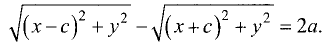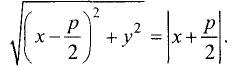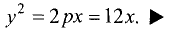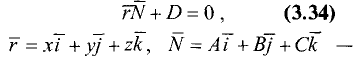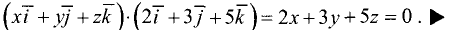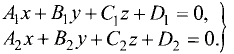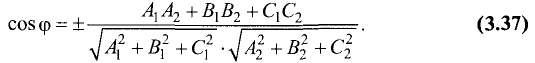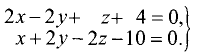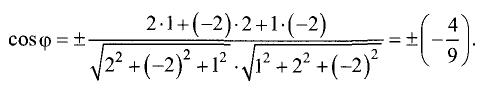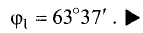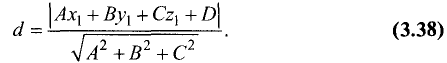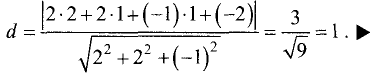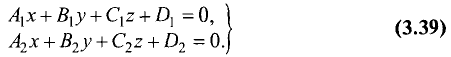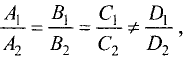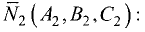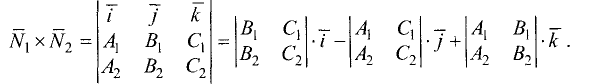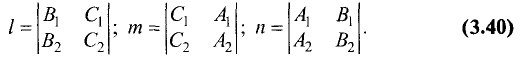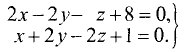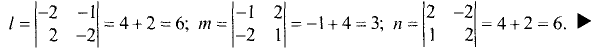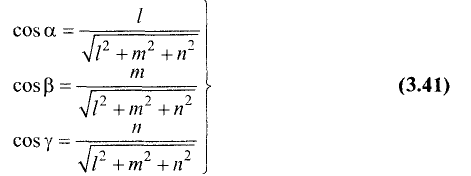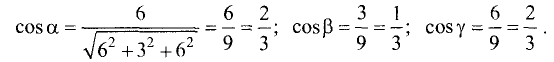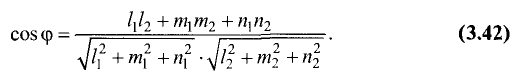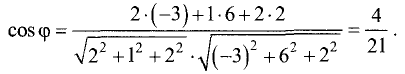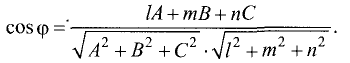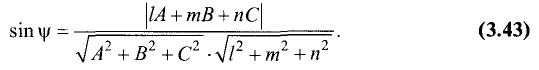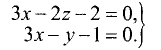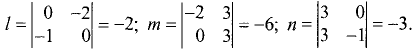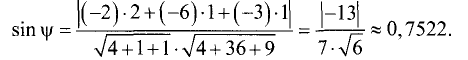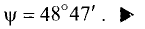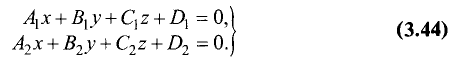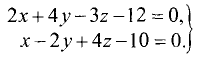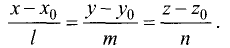- Как найти высоту тетраэдра формула
- Вывод формулы высоты тетраэдра
- Правильный тетраэдр – частный вид тетраэдра
- Вычисление объема тетраэдра, если известны координаты его вершин
- Свойства
- Высоту тетраэдра через векторы
- Контакты
- Объем тетраэдра
- Правильный тетраэдр – частный вид тетраэдра
- Вычисление объема тетраэдра, если известны координаты его вершин
- Аналитическая геометрия — решение задач и выполнение заданий с примерами
- Разложение вектора по базису
- Коллинеарность векторов
- Угол между векторами
- Площадь параллелограмма
- Компланарность векторов
- Объем и высота тетраэдра
- Расстояние от точки до плоскости
- Уравнение плоскости с данным нормальным вектором
- Угол между плоскостями
- Канонические уравнения прямой
- Точка пересечения прямой и плоскости
- Проекция точки на плоскость или прямую
- Симметрия относительно прямой или плоскости
- Геометрия на плоскости
- Системы координат на плоскости
- Прямая линия на плоскости
- Кривые второго порядка
- Преобразование системы координат
- Геометрия в пространстве
- Основные поверхности в пространстве
- Основы аналитической геометрии
- Направленные отрезки
- Прямоугольная система координат
- Деление отрезка в данном отношении
- Угол наклона отрезка к оси абсцисс
- Уравнение прямой
- Условие перпендикулярности прямых
- Угол между прямыми
- Пучок прямых
- Уравнение прямой, проходящей через две данные точки
- Расстояние от точки до прямой
- Уравнение окружности
- Уравнение эллипса
- Уравнение гиперболы
- Уравнение плоскости в трехмерной системе координат
- Уравнение прямой в пространстве
- Найти высоту тетраэдра через вектора
- Контакты
Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Как найти высоту тетраэдра формула
 |
Высота тетраэдра — равна корню квадратному из двух третих, помноженному на длину ребра тетраэдра
(h – высота тетраэдра, a – ребро тетраэдра)
Видео:Высшая математика. 4 урок. Аналитическая геометрия. Вычисление объема тетраэдра.Скачать
Вывод формулы высоты тетраэдра
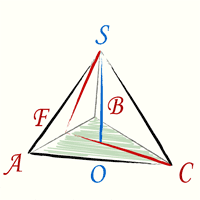
Чтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS:
Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1).
Рассмотрим произвольный треугольник ABC и точку D , не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC . В результате получим треугольники ADC , CDB , ABD . Поверхность ограниченная четырьмя треугольниками ABC , ADC , CDB и ABD называется тетраэдром и обозначается DABC . 
Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра
Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.
Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле
- S – площадь любой грани,
- H – высота, опущенная на эту грань
Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Правильный тетраэдр – частный вид тетраэдра
Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:
- Все грани равны.
- Все плоские углы правильного тетраэдра равны 60°
- Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
- Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).
Пусть нам дан правильный тетраэдр ABCD с ребрами равными a . DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD .
Высота BM равна BM и равна
Рассмотрим треугольник BDM , где DH , являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой

BM=

p=1/2 (BM+BD+DM)=
Подставим эти значения в формулу высоты. Получим
Вынесем 1/2a. Получим

Применим формулу разность квадратов
После небольших преобразований получим 
Объем любого тетраэдра можно рассчитать по формуле 
где 
Подставив эти значения, получим
Таким образом формула объема для правильного тетраэдра
где a –ребро тетраэдра
Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Вычисление объема тетраэдра, если известны координаты его вершин
Пусть нам даны координаты вершин тетраэдра
Из вершины 



Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим 
Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула
Видео:Вычисляем высоту через координаты вершин 1Скачать

Свойства
Зная высоту тетраэдра, можно вычислить его ребро, перевернув формулу так, чтобы ребро было равно корню из трех вторых, умноженному на высоту. a=√(3/2) h
Выразив таким образом ребро тетраэдра через его высоту, можно найти периметр тетраэдра, то есть длину всех его ребер, площадь одной грани и площадь полной поверхности тетраэдра. Периметр тетраэдра будет равен шести длинам его ребер, площадь одной грани – ребру в квадрате, умноженному на корень из трех, деленный на четыре, а площадь полной поверхности – четырем площадям одной грани. P=6a=6√(3/2) h S_1=(√3 a^2)/4=(3√3 h^2)/8 S_(п.п.)=4S_1=(3√3 h^2)/2
Через высоту, подставленную вместо ребра в определенном соотношении можно найти соответственно и радиусы вписанной и описанной окружностей в основание тетраэдра. r=h/(2√2) R=h/√2
Апофема тетраэдра проходит из вершины к противоположной стороне грани под прямым углом и рассчитать ее можно как из прямоугольного треугольника с боковым ребром по той же грани, так и из прямоугольного треугольника во внутреннем пространстве тетраэдра с высотой. l=3h/(2√2)
Чтобы вычислить объем тетраэдра, необходимо возвести в куб ребро и разделить полученное значение на шесть корней из двух, либо подставить вместо ребра корень из трех вторых, умноженный на высоту и преобразовать формулу объема для высоты. V=(√3 h^3)/8
В тетраэдр можно вписать сферу или описать сферу около него, тогда, зная высоту, чтобы вычислить радиусы вписанной и описанной сфер, необходимо воспользоваться следующими, уже готовыми формулами. (рис.60.2, 60.3) r_1=h/4 R_1=3h/4
Видео:Площадь параллелограмма, построенного на данных векторахСкачать

Высоту тетраэдра через векторы
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |
Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
Видео:Задача 6. Вычислить объём тетраэдра с вершинами в точках и его высоту, опущенную из вершины на граньСкачать

Объем тетраэдра
Рассмотрим произвольный треугольник ABC и точку D , не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC . В результате получим треугольники ADC , CDB , ABD . Поверхность ограниченная четырьмя треугольниками ABC , ADC , CDB и ABD называется тетраэдром и обозначается DABC . 
Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра
Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.
Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле
- S – площадь любой грани,
- H – высота, опущенная на эту грань
Видео:Нахождение высоты тетраэдра.Скачать

Правильный тетраэдр – частный вид тетраэдра
Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:
- Все грани равны.
- Все плоские углы правильного тетраэдра равны 60°
- Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
- Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).
Пусть нам дан правильный тетраэдр ABCD с ребрами равными a . DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD .
Высота BM равна BM и равна
Рассмотрим треугольник BDM , где DH , являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой

BM=

p=1/2 (BM+BD+DM)=
Подставим эти значения в формулу высоты. Получим
Вынесем 1/2a. Получим
Применим формулу разность квадратов
После небольших преобразований получим
Объем любого тетраэдра можно рассчитать по формуле 
где 
Подставив эти значения, получим
Таким образом формула объема для правильного тетраэдра
где a –ребро тетраэдра
Видео:§20 Нахождение объёма параллелипипедаСкачать

Вычисление объема тетраэдра, если известны координаты его вершин
Пусть нам даны координаты вершин тетраэдра
Из вершины 



Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим

Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула
Видео:№362. Точка К — середина ребра ВС тетраэдра ABCD. Разложите вектор DK по векторамСкачать

Аналитическая геометрия — решение задач и выполнение заданий с примерами
При изучении аналитической геометрии вы научитесь решать задачи векторной алгебры и использовать свойства линейных операций с геометрическими векторами, скалярного, векторного и смешанного произведений векторов для решения геометрических задач. Вы научитесь решать задачи аналитической геометрии, связанные с различными видами уравнений плоскости и прямой и их взаимным расположением.
Видео:№370. Высоты AM и DN правильного тетраэдра ABCD пересекаются в точке К. Разложите поСкачать

Разложение вектора по базису
Постановка задачи. Найти разложение вектора 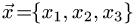
по векторам
1.Искомое разложение вектора 
2.Это векторное уравнение относительно 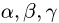
3.Peшaeм эту систему уравнений относительно 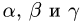
образом определяем коэффициенты разложения вектора 
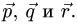
Замечание. Если система уравнений не имеет решений (векторы
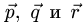

то вектор 
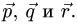
уравнений имеет бесчисленное множество решений (векторы 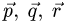


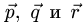
Пример:
Найти разложение вектора 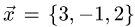
Решение:
1.Искомое разложение вектора 
2.Это векторное уравнение относительно 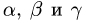
системе трех линейных уравнений с тремя неизвестными
3.Система имеет единственное решение
Ответ.
Видео:№369. Медианы грани ABC тетраэдра ОABC пересекаются в точке М. Разложите вектор ОАСкачать

Коллинеарность векторов
Постановка задачи. Коллинеарны ли векторы 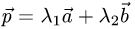
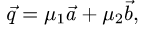
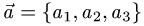
План решения. Векторы коллинеарны тогда и только тогда, когда существует число а такое, что 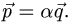
1.Находим координаты векторов 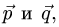
сложении векторов их координаты складываются, а при умножении
на число координаты умножаются на это число.
2.Если координаты векторов 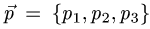
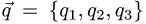
то векторы 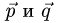
не выполняются, то векторы 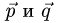
Пример:
Коллинеарны ли векторы 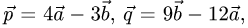
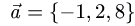
Решение:
1.Находим координаты векторов 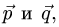
сложении векторов их координаты складываются, а при умножении
на число координаты умножаются на это число:
то координаты пропорциональны. Следовательно, векторы 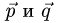
Ответ. Векторы 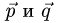
Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Угол между векторами
Постановка задачи. Даны точки 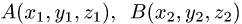
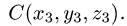
План решения. Косинус угла 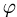
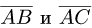
1.Чтобы вычислить длины векторов 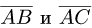
произведение 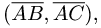
2.По формулам для длины вектора и скалярного произведения
векторов имеем
Вычисляем cos 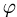
Пример:
Даны точки А(-2,4,-6), В(0,2,-4) и С(-6,8,-10).
Найти косинус угла между векторами
Решение:
1.Находим координаты векторов 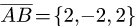
2.По формулам для длины вектора и скалярного произведения
векторов имеем
3.Вычисляем cos 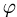
Ответ. Косинус угла между векторами 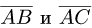
Видео:Решение задач на векторное и смешанное произведения векторовСкачать

Площадь параллелограмма
Постановка задачи. Вычислить площадь параллелограмма, построенного на векторах 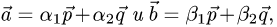
что 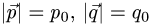
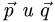
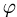
План решения. Площадь параллелограмма, построенного на векторах 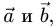
1.Вычисляем 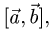
2.Вычисляем модуль векторного произведения
( 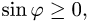
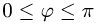
3.Находим площадь параллелограмма, используя формулу(1)
Пример:
Вычислить площадь параллелограмма, построенного на
векторах 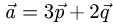
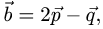
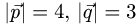
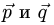
Решение:
1.Вычисляем 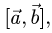
2.Вычисляем модуль векторного произведения
3.Находим площадь параллелограмма, используя формулу (1)
Ответ. Площадь параллелограмма равна 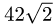
Видео:Вычисление медианы, высоты и угла по координатам вершинСкачать

Компланарность векторов
Постановка задачи. Компланарны ли векторы 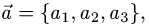
План решения. Для того чтобы три вектора были компланарны
(лежали в одной плоскости или в параллельных плоскостях), необходимо и достаточно, чтобы их смешанное произведение 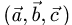
1.Смешанное произведение векторов выражается через их координаты формулой
2.Если определитель в правой части этого равенства равен нулю,
то векторы компланарны, если определитель не равен нулю, то векторы некомпланарны.
Пример:
Компланарны ли векторы 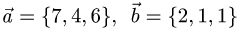
Решение:
1.Вычисляем смешанное произведение векторов:
2.Так как 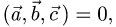
Ответ. Векторы 
Видео:Смешанное произведение векторовСкачать

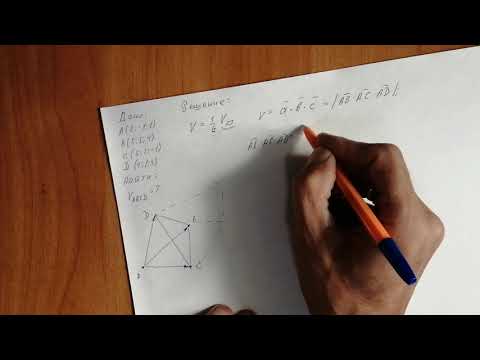
Объем и высота тетраэдра
Постановка задачи. Вычислить объем тетраэдра с вершинами в точках 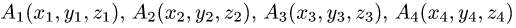
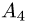
1.Из вершины 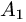
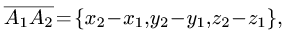
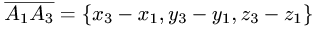
В соответствии с геометрическим смыслом смешанного произведения имеем
где 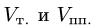
на векторах
С другой стороны,
где согласно геометрическому смыслу векторного произведения
Сравнивая формулы (1) и (2), получаем
2. Вычисляем смешанное произведение
и находим объем тетраэдра по формуле (1).
3. Вычисляем координаты векторного произведения
4. Находим высоту h по формуле (3).
Пример:
Вычислить объем тетраэдра с вершинами 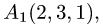
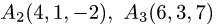
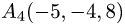
вершины 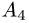
Решение:
1.Из вершины 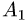
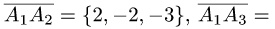
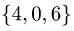
2.Вычисляем смешанное произведение:
и находим объем тетраэдра по формуле (1) 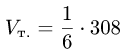
3.Вычисляем координаты векторного произведения:
4.Находим высоту h по формуле (3):
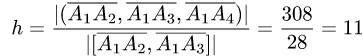
Ответ. 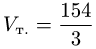
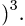
Видео:Тетраэдр. 10 класс.Скачать

Расстояние от точки до плоскости
Постановка задачи. Найти расстояние от точки 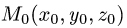
до плоскости, проходящей через точки 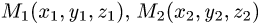
План решения. Искомое расстояние можно найти как высоту
тетраэдра с вершинами 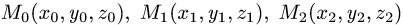
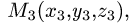
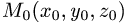
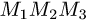
Расстояние d от точки 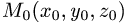
проекции вектора 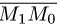
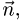
Поскольку нормальный вектор плоскости 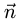
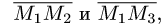
1.Находим координаты векторов:
и нормального вектора плоскости:
2.Вычисляем расстояние d от точки 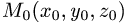
по формуле (1).
Пример:
Найти расстояние от точки 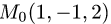
проходящей через точки
Решение:
1.Находим координаты векторов:
и нормального вектора плоскости:
2.Вычисляем расстояние d от точки 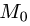
Ответ, d = 7 ед. длины.
Видео:Вычисляем угол через координаты вершинСкачать

Уравнение плоскости с данным нормальным вектором
Постановка задачи. Написать уравнение плоскости, проходящей через точку 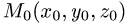
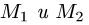
План решения. Уравнение плоскости, проходящей через точку
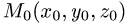
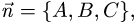
1.В качестве нормального вектора плоскости 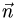
2.Составляем уравнение плоскости (1) с нормальным вектором
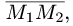
Пример:
Написать уравнение плоскости, проходящей через точку 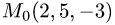
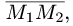
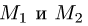
Решение:
1.В качестве нормального вектора плоскости 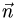
2.Составляем уравнение плоскости (1) с нормальным вектором
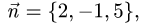
Ответ. Уравнение плоскости 2х — у + 5z + 16 = 0.
Видео:Математика это не ИсламСкачать

Угол между плоскостями
Постановка задачи. Найти угол между плоскостями
План решения. Двугранный угол между плоскостями равен углу
между их нормальными векторами
Поэтому угол 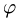
Пример:
Найти угол между плоскостями
х + 2y — 2z — 7 = 0, x + y — 35 = 0.
Решение:
Двугранный угол между плоскостями равен углу между их нормальными векторами 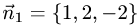
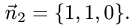
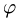
Таким образом,
Ответ. Угол между плоскостями
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Канонические уравнения прямой
Постановка задачи. Написать канонические уравнения прямой, заданной как линия пересечения двух плоскостей (общими уравнениями)
1.Проверяем, что векторы 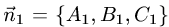
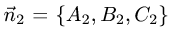
неколлинеарны и, следовательно, плоскости пересекаются по некоторой прямой.
Канонические уравнения прямой с направляющим вектором 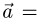
Поэтому чтобы написать уравнения прямой, необходимо найти ее направляющий вектор и какую-нибудь точку на прямой.
2.Так как прямая принадлежит одновременно обеим плоскостям,
то ее направляющий вектор 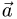
обеих плоскостей, т.е. 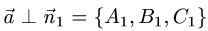
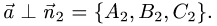
Следовательно, направляющий вектор 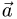
3.Теперь выберем какую-нибудь точку на прямой. Поскольку направляющий вектор прямой непараллелен хотя бы одной из координатных плоскостей, то прямая пересекает эту координатную плоскость. Следовательно, в качестве точки на прямой может быть взята точка ее пересечения с этой координатной плоскостью.
4.Подставляем найденные направляющий вектор и точку в уравнения прямой (1) и записываем ответ.
Пример:
Написать канонические уравнения прямой, заданной
как линия пересечения двух плоскостей (общими уравнениями)
Решение:
1.Проверим, что векторы 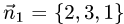
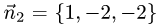
Векторы 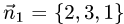
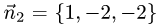
их координаты непропорциональны. Следовательно, две плоскости
пересекаются по прямой.
2.Так как прямая принадлежит одновременно обеим плоскостям,
то ее направляющий вектор 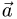
обеих плоскостей, т.е. 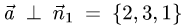
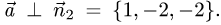
Следовательно, направляющий вектор 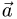
3.Теперь выберем какую-нибудь точку на прямой. Поскольку направляющий вектор прямой непараллелен ни одной из координатных плоскостей, то прямая пересекает все три координатные плоскости.
Следовательно, в качестве точки на прямой может быть взята точка ее пересечения, например, с плоскостью у = 0. Координаты этой
точки находим, решая систему трех уравнений
Получим 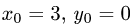
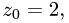
4.Подставляя найденные направляющий вектор и точку в уравнения прямой (1), получим
Ответ. Канонические уравнения прямой имеют вид
Точка пересечения прямой и плоскости
Постановка задачи. Найти точку пересечения прямой
1.Проверим, что прямая не параллельна плоскости. Это означает,
что направляющий вектор прямой 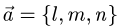
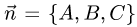
В этом случае существует единственная точка пересечения прямой и
плоскости.
2.Для нахождения точки пересечения прямой и плоскости, вообще
говоря, надо решить систему трех уравнений с тремя неизвестными
(два уравнения прямой и одно уравнение плоскости). Однако удобнее
использовать параметрические уравнения прямой.
Тогда параметрические уравнения прямой имеют вид
3.Подставляя эти выражения для x, у и z в уравнение плоскости
и решая его относительно t, находим значение параметра 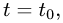
4.Найденное значение 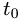
Записываем ответ в таком виде: прямая и плоскость пересекаются
в точке
Пример:
Найти точку пересечения прямой
и плоскости
2x — 3y + z — 8 = 0.
Решение:
Следовательно, направляющий вектор прямой и нормальный вектор
плоскости не ортогональны, т.е. прямая и плоскость пересекаются в
единственной точке.
Тогда параметрические уравнения прямой имеют вид
3.Подставляя эти выражения для x, у и z в уравнение плоскости,
находим значение параметра t, при котором происходит пересечение
прямой и плоскости:
4.Подставляя в параметрические уравнения прямой найденное
значение 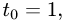
Ответ. Прямая и плоскость пересекаются в точке (3,-1,-1).
Проекция точки на плоскость или прямую
Постановка задачи. Найти координаты проекции 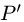
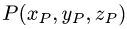
План решения. Проекция Р’ точки Р на плоскость является основанием перпендикуляра, опущенного из точки Р на эту плоскость.
1.Составляем уравнения прямой, проходящей через точку Р перпендикулярно данной плоскости. Для этого в качестве направляющего вектора прямой берем нормальный вектор плоскости: 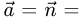
2.Находим координаты точки пересечения Р’ этой прямой с заданной плоскостью (см. задачу 1.11). Положим
Тогда параметрические уравнения прямой имеют вид
3.Подставляя x,y,z в уравнение плоскости и решая его относительно t, находим значение параметра 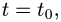
4.Найденное значение 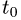
Замечание:
Аналогично решается задача о нахождении координат проекции точки на прямую.
Пример:
Найти координаты проекции Р’ точки Р(1,2, — 1) на
плоскость Зх — у +2z — 4 = 0.
Решение:
1.Составляем уравнения прямой, проходящей через точку Р перпендикулярно данной плоскости. Для этого в качестве направляющего вектора прямой берем нормальный вектор плоскости: 
2.Найдем координаты точки пересечения Р’ этой прямой с задан-
заданной плоскостью. Положим
Тогда параметрические уравнения прямой имеют вид
3.Подставляя эти выражения для х, у и z в уравнение плоскости,
находим значение параметра t, при котором происходит пересечение прямой и плоскости:
4.Подставляя в параметрические уравнения прямой найденное
значение 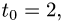
Таким образом, точка пересечения прямой и плоскости и, следовательно, проекция точки Р на плоскость имеет координаты (7, 0,1).
Ответ. Проекция Р’ имеет координаты (7,0,1).
Симметрия относительно прямой или плоскости
Постановка задачи. Найти координаты точки Q, симметричной точке 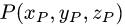
План решения. Искомая точка Q лежит на прямой, перпендикулярной данной и пересекающей ее в точке Р’. Поскольку точка
Р’ делит отрезок PQ пополам, координаты 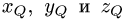
определяются из условий
где 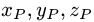
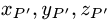
ее проекции Р’ на данную прямую.
1.Найдем проекцию точки Р на данную прямую, т.е. точку Р’
(см. задачу 1.12). Для этого:
а) составим уравнение плоскости, проходящей через точку Р перпендикулярно данной прямой. В качестве нормального вектора 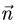
т.е. 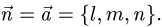
б) найдем координаты точки пересечения Р’ этой плоскости с заданной прямой. Для этого запишем уравнения прямой в параметрической форме
Подставляя х,у, z в уравнение плоскости и решая его относительно t,
находим значение параметра 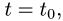
в) найденное значение 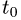
Координаты точки Q, симметричной точке Р относительно данной прямой, определяем из условий (1). Получаем
Замечание. Аналогично решается задача о нахождении координат точки, симметричной данной, относительно плоскости.
Пример:
Найти координаты точки Q, симметричной точке
Р(2, —1,2) относительно прямой
Решение:
1.Найдем проекцию точки Р на данную прямую, т.е. точку 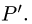
а) составим уравнение плоскости, проходящей через точку Р пер-
перпендикулярно данной прямой. В качестве нормального вектора 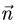
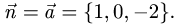
б) найдем точку пересечения заданной прямой и плоскости
x — 2z + 2 = 0. Для этого запишем уравнения прямой в параметрической форме:
Подставляя эти выражения для х, у и z в уравнение плоскости, находим значение параметра t, при котором происходит пересечение
прямой и плоскости: 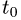
в) подставляя в параметрические уравнения прямой найденное
значение 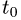
Таким образом, точка пересечения прямой и плоскости и, следовательно, проекция точки Р на прямую есть Р'(0, 0,1).
2.Координаты точки Q, симметричной точке Р относительно дан-
данной прямой, определяются из условий (1):
Геометрия на плоскости
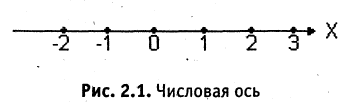
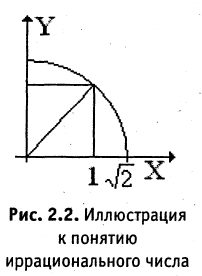
Прямая, для которой указано направление, начало отсчета и масштаб, называется числовой осью. Откладывая целое число единичных отрезков влево и вправо, получим изображение множества целых чисел (рис. 2.1). Если каждый из единичных отрезков оси разделить на n равных частей, то точки деления будут изображать дроби со знаменателем n, эти точки дают изображение всех рациональных чисел типа m/n. Можно доказать, что на любом сколь угодно малом интервале числовой оси всегда находятся рациональные точки. Этот факт выражается так: рациональные точки расположены на числовой оси всюду плотно.
Каждая пара точек m и n, вместе со всеми точками между ними, называется отрезком числовой оси (или сегментом) и обозначается [m, n]. Если же рассматриваются только промежуточные точки между m и n, то говорят о промежутке (или интервале) числовой оси (m, n). Расстояние от точки 0 до точки m есть положительное число, которое называется абсолютной величиной числа m, и обозначается |m|. Расстояние между точками m и n есть положительное число, которое называется длиной отрезка [m,n] и обозначается |m,n|. Пусть отрезок 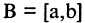
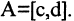
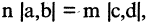
Возьмем квадрат со стороной, равной 1, его диагональ имеет длину 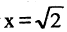

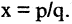
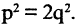

Системы координат на плоскости
Прямоугольная (декартова) система координат на плоскости состоит из двух взаимно перпендикулярных числовых осей, пересекающихся в точке О, называемой началом системы координат. Горизонтальную ось называют осью абсцисс, а вертикальную — осью ординат. Каждой точке плоскости М можно сопоставить ориентированный отрезок ОМ, берущий начало в точке О и оканчивающийся в точке М (см. рис. 2.3). Такой отрезок называют радиус-вектором точки М. Числа 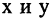
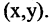
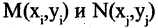
Пример:
Найти расстояние d между двумя точками М(-3,4) и N (5,2). Согласно вышеприведенной формуле, имеем
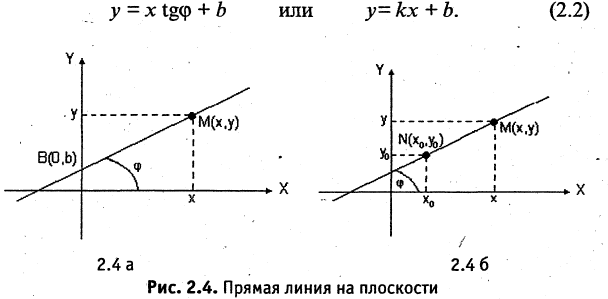
Прямая линия на плоскости
Пусть прямая линия пересекает ось ординат в точке 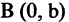
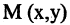
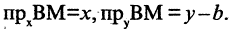
охраняется для всех точек прямой и не выполняется для точек, не принадлежащих прямой. Тангенс угла 
Если 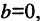
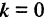
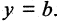
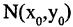
Любое из уравнений прямой можно привести к виду 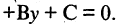
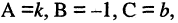
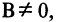
Если 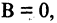
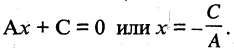
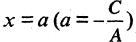
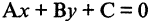
Кривые второго порядка
Кривыми второго порядка называются линии, которые описываются алгебраическими уравнениями второй степени
причем хотя бы один из коэффициентов А, В, С должен быть не равен нулю.
Окружностью называется геометрическое место точек, равноудаленных от данной точки, называемой центром окружности. Уравнение окружности радиуса R с центром в точке М(а, b) имеет вид
Если раскрыть скобки, то мы увидим, что уравнение (2.5) получается из уравнения (2.4), если
Пример:
Пусть задано уравнение 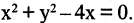
Сравнивая (2.6) с (2.5), видим, что заданное уравнение есть уравнение окружности радиусом 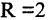
Эллипс — замкнутая кривая, для всех точек которой сумма расстояний до двух фиксированных точек 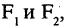
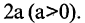
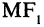
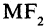
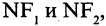
Уравнение эллипса, центр симметрии которого находится в начале координат, а фокусы 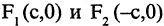
Параметры а и b называются полуосями, причем. 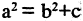
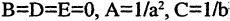
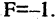
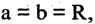
Гипербола — неограниченная кривая, для всех точек которой разность расстояний до двух фиксированных точек, называемых фокусами, есть величина постоянная и по определению равная 2а (рис. 2.7). Разность 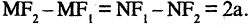
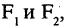
Параметры а и b называются полуосью и мнимой полуосью гиперболы, причем 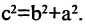
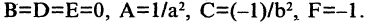
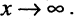
Парабола — неограниченная кривая, все точки которой (см. рис. 2.8) равноудалены от точки, называемой фокусом, и прямой, называемой директрисой, причем расстояние между фокусом и директрисой равно р. Для параболы, изображенной на рис. 2.8, расстояния 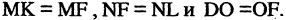
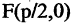
ОХ, а директриса
перпендикулярна ОХ, есть
Уравнение (2.9) получим из (2.4), если 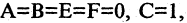
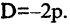
Сделав поворот и сдвиг системы координат, любое уравнение (2.4) можно привести только к одному из трех уравнений второй степени: (2.7), (2.8), (2.9) или к уравнению вида 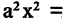
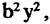
Преобразование системы координат
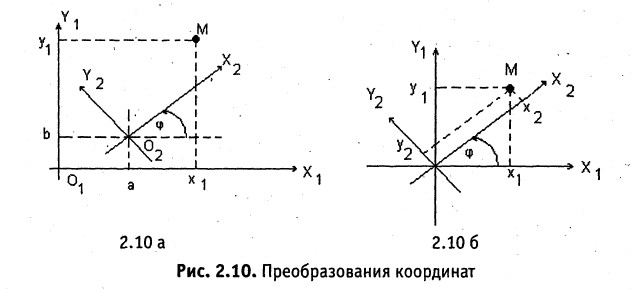
Пусть даны две системы прямоугольных координат 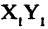
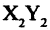
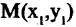
из систем с ее же координатами 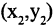
Параллельный перенос системы координат. В первой системе координат точка 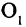
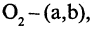
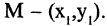
Чтобы получить координаты во второй системе, необходимо провести обратные действия. Это приведет к зависимостям
Поворот системы координат с совмещенной точкой начала. Пусть оси 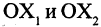
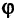
В общем случае связь между координатами точки в различных прямоугольных системах координат выражается линейными соотношениями
Пример:
Как изменятся координаты точки М(-2,3), если система будет повернута на 30° и сдвинута вверх на две единицы?
Применяя формулы (2.12) для 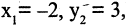
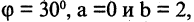
Для определения положения точек на плоскости часто применяется так называемая полярная система координат. Выберем на плоскости фиксированную точку О, называемую полюсом, и исходящую из нее ось ОР, называемую полярной осью. На полярной оси выбрана единица масштаба. В этой систем как показано на рис. 2.11, положение точки М на плоскость вполне задается отрезком ОМ, называемым полярным радиусом точки М, равным расстоянию отрезка ОМ, и углом 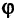
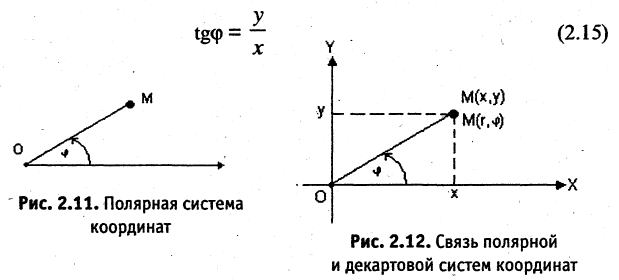
Если на плоскости заданы прямоугольная и полярная системы координат, причем начало координат и положительная часть оси абсцисс прямоугольной системы совпадают соответственно с полюсом и осью полярной системы координат (рис. 2.12), то декартовы и полярные координаты точки М связаны соотношением
Формулы (2.13) выражают координаты точки М в прямоугольной системе через ее же координаты в полярной системе. Отсюда
Геометрия в пространстве
Системы координат в пространстве:
Прямоугольная (декартова) система координат в пространстве возникает, если взяты три одинаковые взаимно перпендикулярные числовые оси — оси координат, которые пересекаются в точке О, называемой началом системы координат. Первую ось ОХ называют осью абсцисс, вторую ось ОY — осью ординат, третью ОХ — осью аппликат. Через каждые две (из трех) координатные оси проходит координатная плоскость.
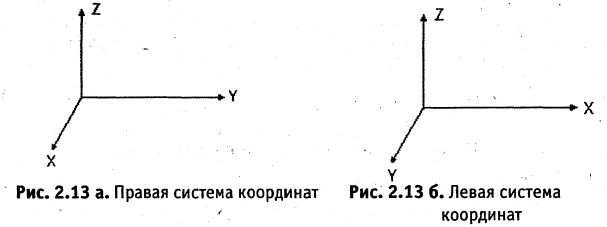
Существуют две, не сводящиеся друг к другу системы координат: правая система координат и левая система координат. Различить эти системы координат можно следующим образом: если посмотреть из любой положительной точки оси ОZ на ось ОY и ось ОХ окажется справа, то это правая система координат, если слева — левая (сравните рис. 2.13 а и рис. 2.13 6).
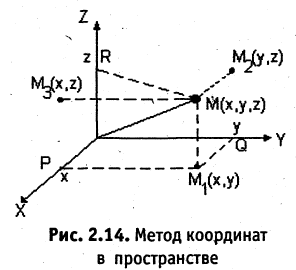
Каждой пространственной точке М можно сопоставить ориентированный отрезок ОМ, берущий начало в точке начала координат и оканчивающийся в точке М (см. рис. 2.14). Такой отрезок называют радиус-вектором точки М. Спроектируем точку М на оси координат. Каждой точке М соответствуют три точки на осях (на рис. 2.14 Р, Q, R) их координаты называют координатами точки М. Они однозначно определяют положение этой точки в выбранной системе координат. Наоборот, задав на каждой из осей координат по одной точке, например, Р, Q, и R, мы определим одну и только одну точку в пространстве (на рис. 2.14 точка М). Эта точка получается при пересечении трех взаимно перпендикулярных плоскостей 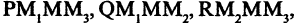
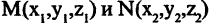
Например, расстояние между двумя точками М(2,-1,3) и N(-2,-1,0), согласно (2.16), равно
В пространстве всякая поверхность может рассматриваться как некоторое множество точек, между координатами которых установлены определенные соответствия
Основные поверхности в пространстве
- Плоскость в пространстве. Наиболее простой вид уравнения (2.17) — уравнение, линейное относительно всех неизвестных
которое описывает плоскость в пространстве. Если
то уравнение
описывает плоскость, проходящую через начало координат (см. главу 2.4).
2. Цилиндрические поверхности — это поверхности, описываемые прямой, называемой образующей, двигающейся параллельно фиксированной заданной прямой и пересекающей некоторую линию L, называемую направляющей цилиндрической поверхности. Направляющая линия не обязательно замкнута. В частности, если образующая параллельна оси ОZ, то уравнение такой цилиндрической поверхности описывается уравнением, не содержащим z
В этом случае вид функции F определяет направляющую линию цилиндра. Так, (см. рис. 2.5 а, б, в)) в пространстве
уравнение 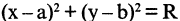
уравнение 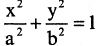
уравнение 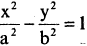
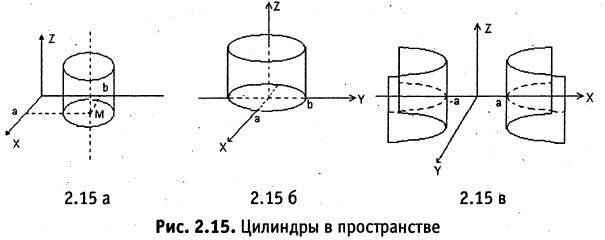
Пример:
Какую поверхность определяет следующее уравнение:
Решение. Выделим полные квадраты в левой части уравнения: 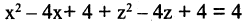
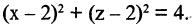
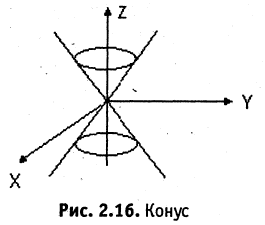
3. Конические поверхности. Поверхность, описываемая прямой (образующая конической поверхности), проходящей через данную точку, называемую вершиной, и пересекающей данную линию (направляющую конуса), называется конической поверхностью.
Наиболее простой формулой описывается конус, имеющий вершину в начале координат, а его образующая описывает вокруг оси координат некоторую замкнутую кривую, например, как показано на рис. 2.16, эллипс. Уравнение такого конуса имеет вид
Пример:
Найти уравнение поверхности, возникающей при вращении прямой 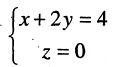
Решение. При вращении прямой возникнет коническая поверхность. Вершиной конуса будет являться точка пересечения его образующей с осью ОХ с координатами 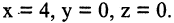
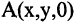
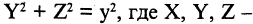
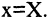
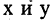
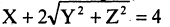
4. Сфера есть геометрическое место точек в пространстве, равноудаленных от одной точки, называемой центром. Величина удаления точек сферы от центра есть расстояние от точки центра до точек сферы.
Следовательно, используя (2.16), можно записать уравнение сферы
где r — радиус сферы или расстояние от произвольной точки сферы 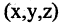
5. Поверхности вращения. Пусть в плоскости YОZ лежит кривая, уравнение которой 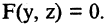
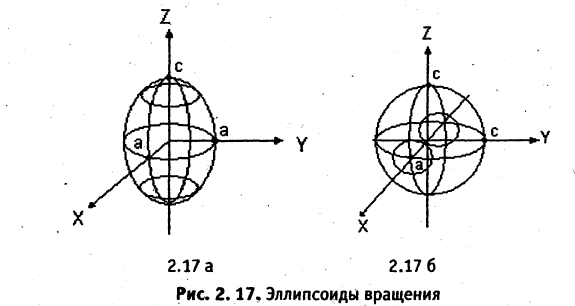
При анализе поверхностей вращения в каждом конкретном случае необходимо указывать, в какой плоскости лежит образующая кривая и вокруг какой оси она вращается. Так, например, эллипсоид вращения, описываемый уравнением
образован вращением вокруг оси ОZ эллипса, лежащего в плоскости ХОZ (рис. 2.17 а). Если этот же эллипс вращать вокруг оси ОХ, то уравнение соответствующего эллипсоида вращения (рис. 2.17 б) имеет вид
Пример:
Записать уравнение эллипсоида вращения, полученного от вращения эллипса вокруг оси ОY, если на его поверхности лежат точки А(3,0,0) и В(0,2,0).
Решение:
Заданные точки лежат в координатной плоскости ХОY и определяют вершины эллипса 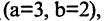
Линию в пространстве образует пересечение двух поверхностей. Отсюда следует, что пространственную линию можно описать системой двух уравнений
Пример:
Найти линию, образуемую пересечением плоскости 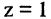
Решение:
Искомая линия находится как решение системы этих уравнений
Решение этой системы есть уравнение окружности 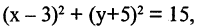
Пересечение трех поверхностей может давать просто точку в пространстве. Математически это соответствует единственному решению системы трех уравнений
Если система (2.20) несовместна, то это означает, что поверхности, описываемые данными уравнениями, не пересекаются в одной точке.
Основы аналитической геометрии
Направленные отрезки
Положение точки на прямой линии определяется одной координатой.
Одно из двух взаимных направлений данной прямой (безразлично какое) называется положительным и обозначается стрелкой.
Противоположное направление называется отрицательным (рис. 3.1).
За начало координат принимают точку О (ноль). Прямую обычно
называют какой-либо буквой, например X. За единицу масштаба
принимают какой-либо отрезок прямой, например ОЕ = 1. Координатой точки М, лежащей на прямой, является длина отрезка ОМ со знаком «плюс», если точка М удалена в положительном направлении от точки О, и со знаком «минус», если точка М удалена в
отрицательном направлении от точки О, т.е. координату точки М можно представить в виде
Пример:
Обозначить на координатной оси ОХ точки,
имеющие координаты:
Решение:
Выбираем масштаб, имеющий длину 
Точки с указанными координатами представлены на рис. 3.2. ►
Направленный отрезок характеризуется длиной и направлением
(рис. 3.3). Отрезок начинается в точке А и заканчивается в точке
В. Обозначается
Направленные отрезки 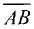
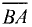
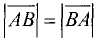
противоположны по направлению.
Если известны координаты начала 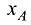
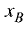
его длина рассчитывается по формуле
Пример:
Найти длину отрезка с координатами начала и
конца, представленными в табл. 3.1.
Таблица 3.1
Решение:
Результаты расчета представлены в табл. 3.2.
Таблица 3.2
Знак «минус» перед значением длины отрезка указывает на
направление отрезка, противоположное направлению оси.
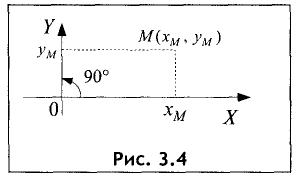
Прямоугольная система координат
Положение точки на поверхности (плоскость, поверхность шара
и т. д.) определяется двумя координатами (рис. 3.4).
Прямоугольная система координат на плоскости представляет из
себя две перпендикулярные прямые, снабженные масштабами и
направлениями. Такие прямые называются координатными осями.
Координатами точки называются координаты оснований
перпендикуляров, опущенных из этой точки на координатные оси (рис. 3.4).
Ось ОХ называется осью абсцисс, а ось OY — осью ординат.
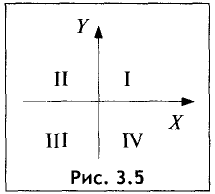
Четыре угла, образуемые осями координат, называются координатными углами и обозначаются I, II, III, IV (рис. 3.5).
Если не требовать перпендикулярности осей координат, то получим более общую систему декартовых координат.
Прямоугольная система координат является частным случаем декартовой.
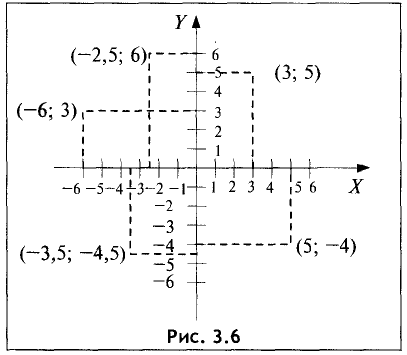
Пример:
Построить на плоскости в прямоугольной системе координат точки, имеющие следующие координаты: (3; 5), (—2,5; 6),
(5; -4), (-3,5; -4,5), (-6; 3).
Решение:
Указанные точки представлены на
рис. 3.6. ►
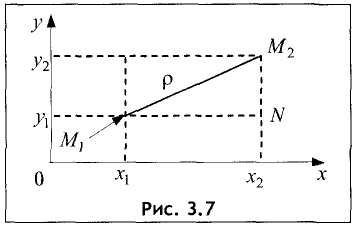
Расстояние 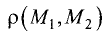
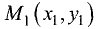
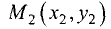
Действительно, проведем через каждую из точек 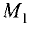
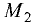
Отсюда следует, что треугольник 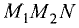
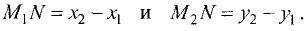
Поэтому гипотенуза равна
что и требовалось доказать.
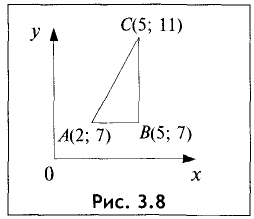
Пример:
Найти периметр треугольника ABC по следующим
данным: А(2; 7), В(5; 7), С(5; 11).
Решение:
Исследуемый треугольник
представлен на рис. 3.8.
Прямая АВ равноудалена от оси Ох, поэтому она параллельна этой оси. По этой же причине прямая ВС параллельна оси Оу. Поэтому АВ и ВС перпендикулярны, т.е. треугольник ABC — прямоугольный. Таким образом, АВ= 5 — 2 = 3, ВС= 11 -7 = 4,
Периметр треугольника П=3 + 4 + 5= 12. ►
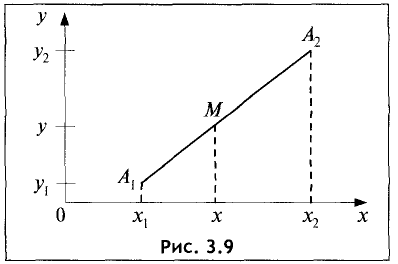
Деление отрезка в данном отношении
Даны точки 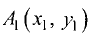
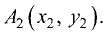
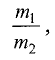
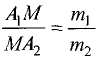
Прямые, проведенные из точек 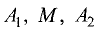
Ох, делят прямые Ох и 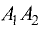
Преобразуем это выражение к виду
Точка M может быть расположена и вне отрезка 
В этом случае отношение 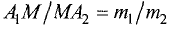
величиной, так как отрезки 
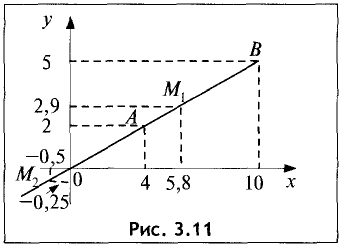
Пример:
Даны точки А(4; 2), В(10; 5). Найти точки 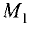
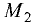
делящие отрезок в отношении 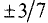
Решение:
Геометрия задачи представлена на рис. 3.11.
При делении отрезка внутренним образом координаты точки 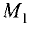
При делении отрезка внешним образом координаты точки 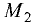
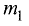
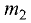
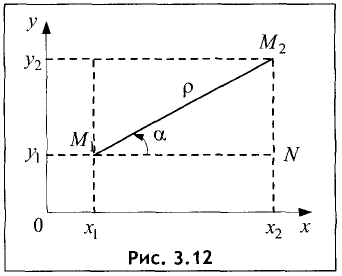
Угол наклона отрезка к оси абсцисс
Проведем через точки 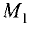
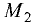
Оу, и две прямые, параллельные оси Ох (рис. 3.12).
Отрезок 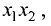
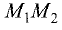
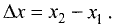
Из прямоугольного треугольника 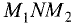
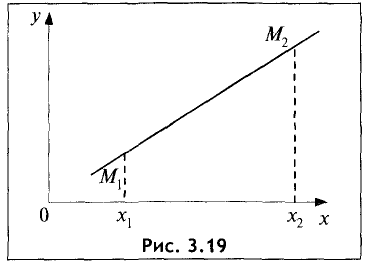
Уравнение прямой
В общем случае уравнение прямой записывают в виде
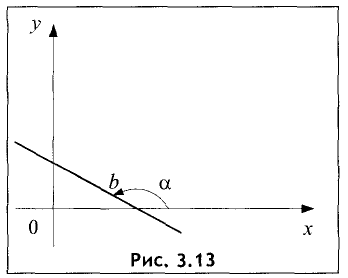
Ах + Ву + С = 0. (3.3)
Преобразуем это уравнение относительно у:
Это наиболее часто встречаемый вид уравнения прямой. Графически прямая представлена на рис. 3.13.
Коэффициент К, входящий в уравнение прямой, называется угловым коэффициентом и равен тангенсу угла между осью Ох и прямой K=tg a (рис. 3.13).
Коэффициент b — это координата точки пересечения прямой с осью Оу. В этом легко убедиться, положив х = 0, т.е.
Уравнение прямой, параллельной оси Ох, следует из уравнения (3.4) при К = tg а = tg 0 = 0 и имеет вид
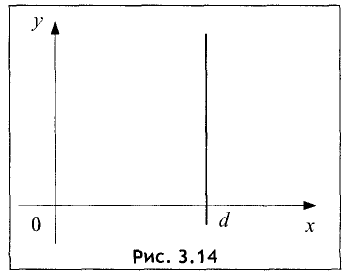
Уравнение прямой, параллельной оси Оу, следует из общего уравнения прямой (3.3) при b = 0. Тогда Ах + С = 0 . Решив это уравнение относительно х, получим
График этой прямой представлен на рис. 3.14
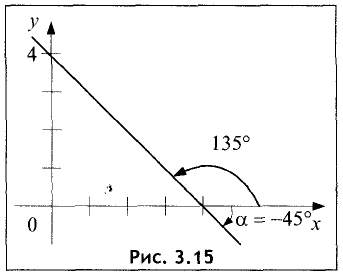
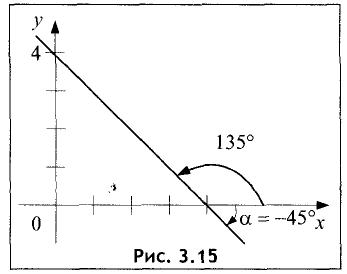
Пример:
Написать уравнение прямой, образующей с осью абсцисс угол 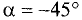
Решение:
Положительное направление угла отсчитывается от оси Ох против часовой стрелки, а отрицательное — по часовой стрелке (рис. 3.15).
Угловой коэффициент К=tg(-45)°=tgl35° = -1. Уравнение прямой имеет вид у=-х+4.
Точка пересечения прямой с осью ОХ находится из условия у=0. Ее координата равна х=4. График прямой предоставлен на рис. 3.15. ►
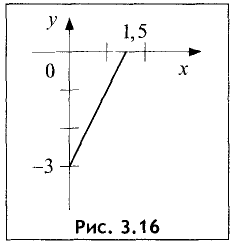
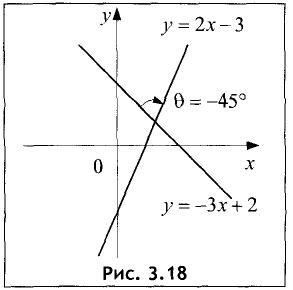
Пример:
Начертить график прямой у=2х-3.
Решение:
Ось Оу прямая пересекает в точке у=-3, а ось Ох — в точке х=32=1,5. Отметив на осях оказанные координаты, проводим прямую через две точки (рис. 3.16) ►
Пример:
Найти точку пересечения двух прямых:
Решение:
Точкой пересечения является решение системы из двух линейных уравнений (3.7). Вычитая из второго уравнения первое, получим 2х— 3+х — 4 = 0. Решив это уравнение, получим абсциссу точки пересечения прямых: х = 7/3.
Подставив значение абсциссы точки пересечения прямых в первое уравнение (3.7), получим значение ординаты точки пересечения, т.е.
Условие перпендикулярности прямых
Даны две прямые
Если эти прямые перпендикулярны, то угол наклона одной из них должен отличаться от угла наклона другой на 90°, т.е. 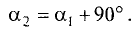
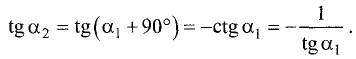
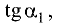
Пример:
Найти угол наклона прямой, перпендикулярной к прямой у = х +1.
Решение:
Так как 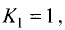
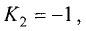
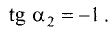
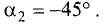
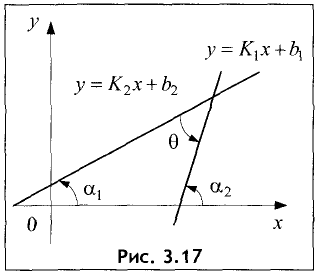
Угол между прямыми
Пусть две прямые заданы уравнениями:
Если угол между прямыми равен 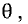
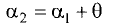
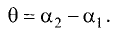
Пример:
Найти угол, образованный прямой у = -3х + 2 с прямой у = 2х
Решение:
Так как 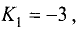
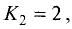
Отсюда находим 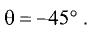
Пучок прямых
Совокупность всех прямых, проходящих через данную точку 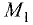
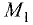
в котором угловой коэффициент К рассматривается как величина, способная принимать любые числовые значения, называется уравнением пучка с центром 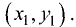
Пример:
Указать точку, через которую проходят все прямые, представленные уравнением y + 3 = K(x + 1).
Решение:
Сопоставив уравнение примера с (3.10), определим координаты центра, равные (-1; -3). ►
В общем виде уравнение пучка прямых можно записать в виде
Найдем уравнение прямой, перпендикулярной прямой
Пусть уравнение искомой прямой имеет вид
Если 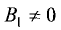
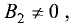
Используя (3.8), условие перпендикулярности двух рассматриваемых прямых можно представить в виде
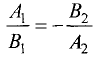
Условие (3.13) будет выполняться, если положить 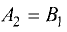

Уравнение прямой, проходящей через две данные точки
Пусть имеются две точки 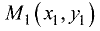
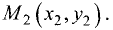
Уравнение пучка прямых, проходящих через точку 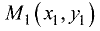
Одна из этих прямых проходит также через точку 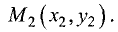
Из полученного уравнения определяем угловой коэффициент искомой прямой.
Подставив полученную формулу для углового коэффициента в уравнение пучка прямых, найдем
Окончательно уравнение прямой, проходящей через две заданные точки, записывают в виде
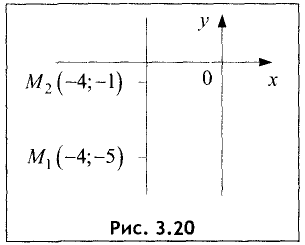
Пример:
Составить уравнение прямой, проходящей через
точки: а) 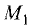
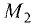
Решение:
а) Подставив данные примера в (3.15), найдем 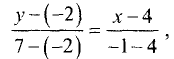
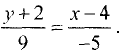
б) подставив данные в (3.15), получим 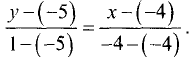
знаменатель в правой части равен нулю, а на ноль делить нельзя, то эта прямая параллельна оси Оу, что и следует из рис. 3.20.
Уравнение искомой прямой имеет вид х = -4 . ►
Пример:
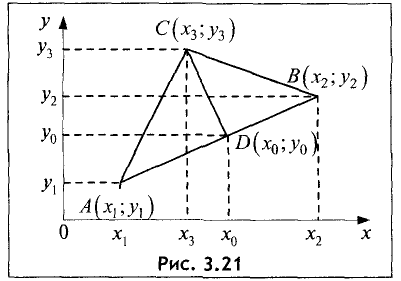
Определить площадь S треугольника АВС с вершинами 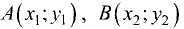
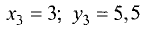
Решение:
Площадь треугольника определяем по формуле
где 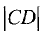
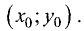
через точки А и В, имеет вид
а ее угловой коэффициент определяется формулой
Таким образом, уравнение прямой, проходящей через точки А и В,
можно представить в виде
Угловой коэффициент прямой, перпендикулярной к рассматриваемой, определяем по формуле
Уравнение данной прямой имеет вид
Координаты точки D находим из системы двух линейных уравнений:
Вычитая из второго уравнения первое, получим
Для условий примера имеем
Определим высоту треугольника
Площадь треугольника равна
Расстояние от точки до прямой
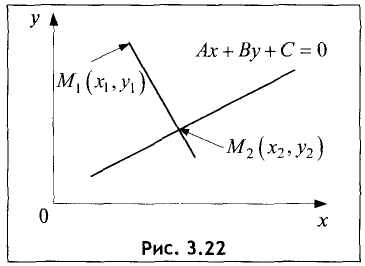
Найти расстояние d от данной точки 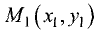
Ах + Ву + С = 0. (3.16)
Расстояние d находим по формуле (рис. 3.22):
Точка 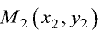
опущенного из точки 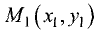
В соответствии с (3.14) уравнение прямой, перпендикулярной (3.16), имеет вид
Координаты точки 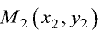
Введем замену: 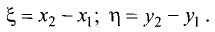
можно записать в виде
Решая систему из двух последних уравнений, находим
Подставив эти значения в (3.19), получим
Пример:
Найти расстояние от точки М (—1; 1) до прямой
Решение:
Искомое расстояние находится по формуле (3.20):
Уравнение окружности
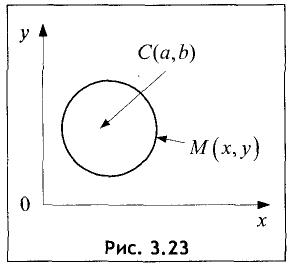
Пусть дана окружность радиуса R с координатами центра C(a,b) (рис.
3.23).
Найдем ее уравнение. По определению окружности для С(а,b) любой ее точки М(а,b) расстояние от центра до этой точки постоянно и
равно радиусу окружности R. Как следует из формулы (3.1), это
расстояние равно
Возводя в квадрат правую и левую части этого равенства,
получим уравнение окружности
Если центр окружности лежит в начале координат, то а = b = 0 ,
а уравнение окружности приобретает вид
если хотя бы одна из трех величин А, В или С не равна нулю,
называется уравнением второго порядка, а линия, представляемая таким уравнением, — линией второго порядка. Выясним, при каких
условиях это уравнение является уравнением окружности. Для этих целей уравнение (3.21) представим в виде
В уравнении (3.22) положим 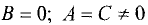
и левую части на А. В результате получим
Уравнение (3.24) имеет тот же вид, что и уравнение (3.23), т.е.
является уравнением окружности. Сопоставив (3.23) с (3.24), найдем
Пример:
Является ли уравнение 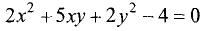
окружностью?
Решение:
Не является, так как в нем содержится слагаемое,
содержащее ху. ►
Пример:
Является ли уравнение 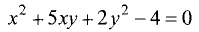
окружностью?
Решение:
Не является, так как коэффициенты при 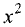
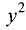
равны. ►
Пример:
Найти координаты центра и радиус окружности
Решение:
Преобразуем исходное уравнение следующим образом:
1. Делим правую и левую части на 2:
2.Дополняем выражения 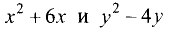
3.Приводим уравнение к виду (3.21):
Отсюда следует, что исходное уравнение является окружностью
радиуса 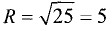
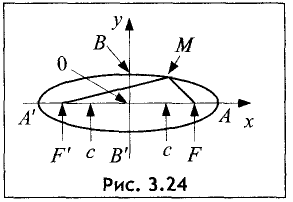
Уравнение эллипса
Эллипсом называется геометрическое место точек, для которых сумма расстояний для двух точек F и F’ равна постоянной величине 2а.
Пусть две точки F и F’ отстоят на расстояние 2с друг от друга
(рис. 3.24).
Сумма расстояний 2а от этих точек до любой точки эллипса
всегда больше 2с. В противном случае искомого геометрического места точек не существует. Найти уравнение эллипса.
Принимаем прямую FF’ за ось абсцисс, середину отрезка FF’ —
за начало координат. Тогда координаты точек F и F’ примут
значения
По определению эллипса сумма расстояний для двух точек
F и F’ равна постоянной величине 2а, т.е.
Перепишем его в виде
Возведем в квадрат левую и правую части последнего равенства
и сгруппируем члены:
Сократим на 4, возведем в квадрат и приведем подобные члены
Разделив правую и левую части на 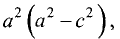
уравнение эллипса:
Из определения эллипса и геометрии рис. 3.24 следует, что при
совмещении точки М с точкой А большая ось эллипса А’А = 2а , т.е.
большая полуось равна а. Введем обозначение
Тогда уравнение эллипса принимает вид
Как следует из треугольника OBF и соотношения (3.26), малая
полуось эллипса ОВ равна b.
Точки F и F’ называются фокусами эллипса, а расстояние FF’ = 2с — фокусным расстоянием. Отношение фокусного расстояния к большой оси называется эксцентриситетом эллипса и обозначается буквой 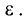
Пример:
Определить эксцентриситет окружности.
Решение:
Так как в окружности а = b, то, как следует из соотношения (3.21), с = 0, т.е. 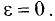
Пример:
Фокусное расстояние эллипса равно 8 см, малая ось
равна 6 см. Найти большую ось и эксцентриситет.
Решение:
Так как фокусное расстояние FF’ = 2с = 8 , то с = 4, а
малая полуось b=3. Из соотношения (3.26) находим длину большой
полуоси:
Большая ось равна 2а = 10 см.
Эксцентриситет находим по формуле
Уравнение гиперболы
Гиперболой называется геометрическое место точек М, для которых
разность расстояний до двух точек F и F’, называемых фокусами, имеет одну и ту же абсолютную величину 2а.
Пусть две точки F и F’ отстоят на расстояние 2с друг от друга (рис. 3.25).
Разность расстояний 2а от этих точек до любой точки гиперболы
всегда меньше 2с. В противном случае искомого геометрического места точек не существует. Найти уравнение гиперболы.
Принимаем прямую FF’ за ось абсцисс, середину отрезка FF’ —
за начало координат. Тогда координаты точек F и F’ примут значения
По определению гиперболы разность расстояний для двух точек
F и F’ равна постоянной величине 2а, т.е. для правой ветви
для левой ветви
Проведя те же преобразования, что и в предыдущем параграфе,
получим
В отличие от эллипса здесь разность 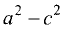
как а Уравнение параболы
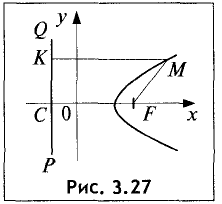
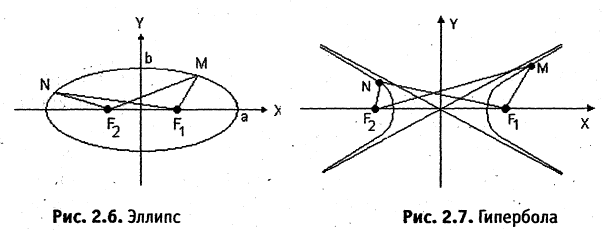
Параболой называется геометрическое место точек М, равноудаленных от данной точки F, называемой фокусом, и прямой PQ, называемой директрисой параболы. Расстояние FC = р от фокуса до директрисы называется параметром параболы.
Пусть прямая PQ и точка F отстоят на расстоянии р от искомого геометрического места точек (рис. 3.27).
Найти уравнение параболы.
Примем за начало координат середину отрезка CF. 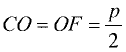
Тогда фокус F будет иметь следующие координаты: 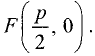
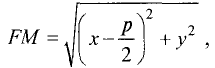
расстояние КМ — выражением 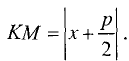
параболы эти два расстояния равны друг другу, т.е.
Данное выражение является уравнением параболы. Возведя
левую и правую части в квадрат и приведя подобные члены, получим каноническое уравнение параболы:
Пучок лучей с источником, расположенном в фокусе, после
отражения от параболы обратится в параллельный пучок лучей. На
этом принципе построены параболические зеркальные антенны.
Пример:
Написать каноническое уравнение параболы с
фокусным расстоянием, равным 3.
Решение:
Так как фокусное расстояние равно 3, то параметр
параболы р = 2 • 3 = 6. Используя уравнение (3.32), получим
каноническое уравнение параболы
Уравнение плоскости в трехмерной системе координат
Положение точки в пространстве определяется тремя координатами.
Прямоугольная система координат в пространстве представляет
из себя три перпендикулярные прямые, снабженные масштабами и
направлениями. Такие прямые называются координатными осями.
Координатами точки называются координаты оснований
перпендикуляров, опущенных из этой точки на координатные оси.
Всякое уравнение, линейное относительно координат, определяет плоскость, и, наоборот, уравнение любой плоскости есть уравнение первой степени.
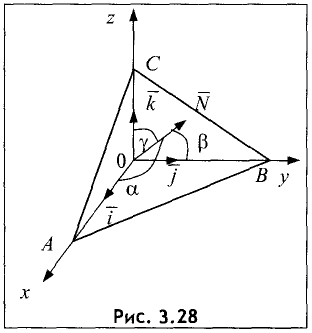
Общее уравнение плоскости имеет вид (рис. 3.28)
Ax + By + Cz + D = 0. (3.33)
Уравнение плоскости может быть представлено в векторной
форме
вектор, перпендикулярный плоскости.
Если D = 0, то плоскость проходит через начало координат.
Если A = 0 (В = 0,С = 0), то плоскость параллельна относительно оси Ox (Оу, Oz).
Пример:
Составить уравнение плоскости, проходящей через
начало координат и перпендикулярной вектору
Решение:
Из (3.34) следует, что уравнение плоскости, проходящей через начало координат, определяется соотношением 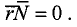
Поэтому искомое уравнение имеет вид
Нормальное уравнение плоскости имеет вид
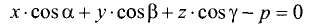
где 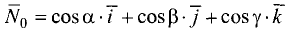
Уравнение плоскости в отрезках:
где а, b и с — отрезки, отсекаемые плоскостью на осях координат с
учетом знака.
Пример:
Составить уравнение плоскости, отсекающей от
каждой оси одинаковое число линейных единиц.
Решение:
Так как а = b = с , то уравнение плоскости имеет вид
Две плоскости, представляемые уравнениями
образуют четыре двугранных угла, равных попарно. Когда говорят
об угле между двумя плоскостями, то имеют в виду любой из этих
углов и приписывают ему значение 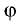
Одно из значений 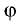
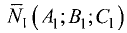
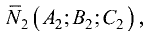
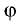
Пример:
Найти угол между плоскостями, заданными
уравнениями
Решение:
Подставив в (3.38) соответствующие коэффициенты,
получим
Таким образом, 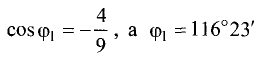
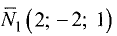
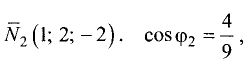
Расстояние от точки 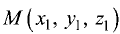
Ax + By + Cz + D = 0
определяется по формуле
Пример:
Найти расстояние от точки М (2,1,1) до плоскости
Решение:
Подставив исходные данные в формулу (3.38), получим
Уравнение прямой в пространстве
Всякая прямая линия представляется системой двух уравнений
первой степени
которые, взятые по отдельности, представляют какие-либо две
плоскости, проходящие через эту прямую.
Если коэффициенты 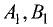
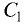
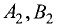
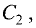
то плоскости параллельны и никогда не пересекутся, т.е. такая
система не представляет прямой линии.
Направляющим вектором прямой называется всякий ненулевой вектор 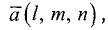
За направляющий вектор прямой (3.39) можно принять векторное
произведение нормальных векторов 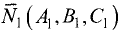
Пример:
Найти направляющие коэффициенты прямой
Решение:
По формулам (3.40) находим
Под углами 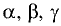
углы между направляющим вектором 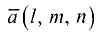
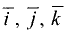
соответственно. Косинусы этих углов вычисляются по формулам
Пример:
Для условий примера 3.27 найти направляющие
косинусы и углы, образуемые прямой с осями координат.
Решение:
По формулам (3.41) находим
Находя арккосинусы, получим
Под углом между двумя прямыми понимается угол между их
направляющими векторами 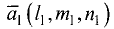
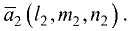
зависимости от выбора направления векторов (каждый из них может иметь два взаимно противоположных направления) этот угол может иметь два значения, дополняющих друг друга до 180°. Косинус угла между прямыми вычисляется по формуле
Пример:
Даны две прямые с направляющими векторами 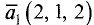
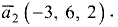
Решение:
Подставим данные примера в формулу (3.42):
Отсюда находим
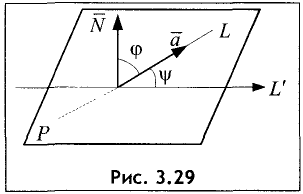
Углом между прямой L и плоскостью Р называют острый угол 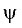
между прямой L и ее проекцией L’
на плоскость Р (рис. 3.29).
Пусть даны направляющий вектор 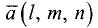
нормальный вектор 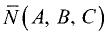
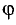
Как следует из рис. 3.29, 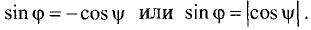
Пример:
Найти угол между прямой
и плоскостью 2x + y + z + 5—0.
Решение:
Направляющими коэффициентами прямой являются числа
Координаты нормального вектора плоскости:
Подставив полученные цифры в (3.43), найдем
Отсюда следует
(коэффициенты 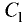
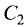
координатную плоскость хОу находится по следующему правилу: чтобы найти проекцию прямой (3.44) на координатную плоскость хОу
достаточно исключить z из уравнений (3.44); полученное
уравнение совместно с уравнением z = 0 представляет искомую
проекцию.
Аналогично находятся проекции прямой на координатные
плоскости yOz и zOx.
Пример:
Найти проекции прямой
на координатные плоскости.
Решение:
Исключив z из системы уравнений, получим уравнение проекции данной прямой на плоскость хОу :
Исключив у из системы уравнений, получим уравнение проекции
данной прямой на плоскость zOx :
Исключив х из системы уравнений, получим уравнение проекции
данной прямой на плоскость yOz :
Пусть задан направляющий вектор 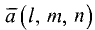
проходящий через точку 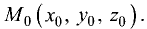
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Найти высоту тетраэдра через вектора
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |













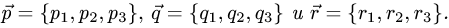
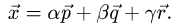
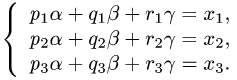
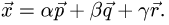
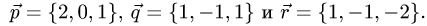
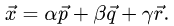
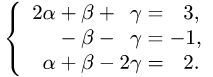
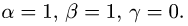
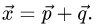
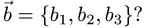
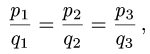
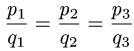
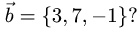
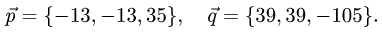
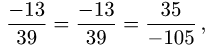
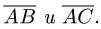
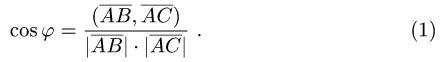
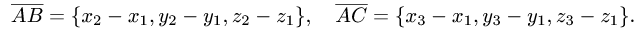
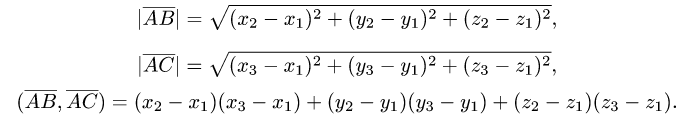
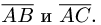
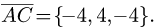
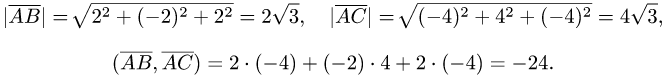
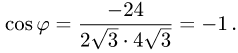


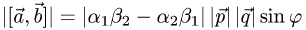
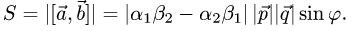
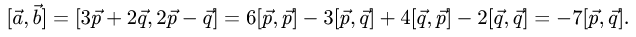
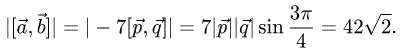
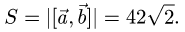
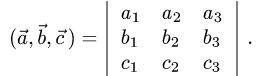
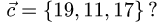

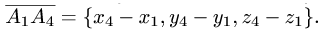
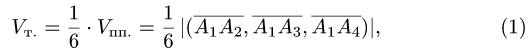
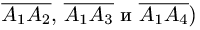
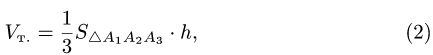
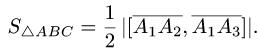
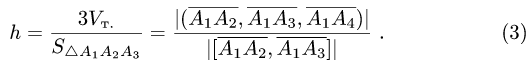
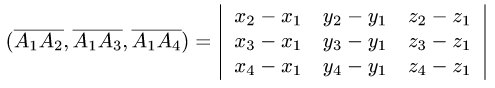
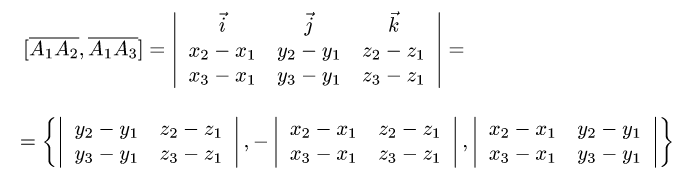
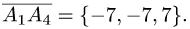
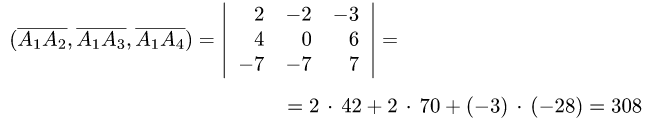
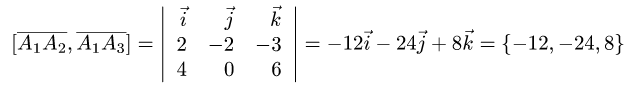
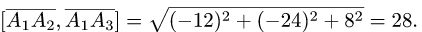
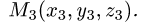
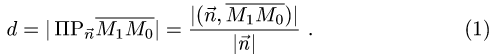
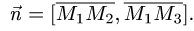
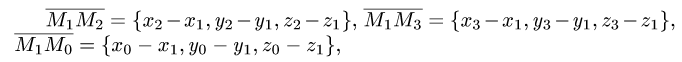
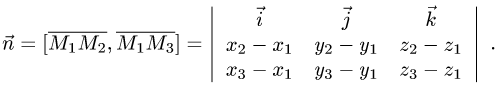
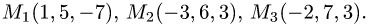
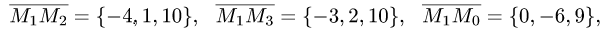
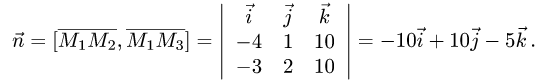
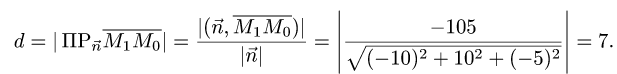
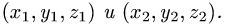
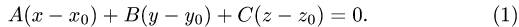
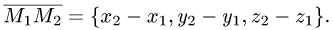
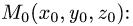
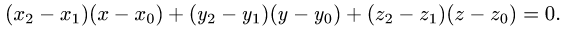
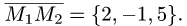
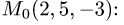
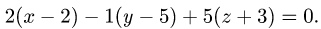
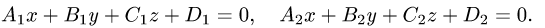
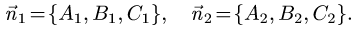
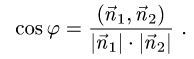
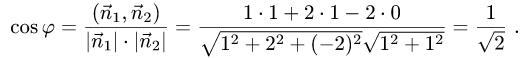
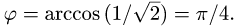
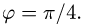
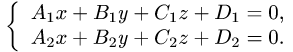
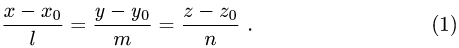
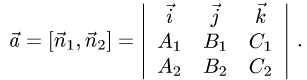
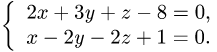
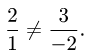
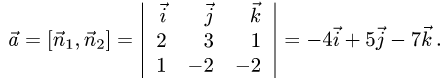
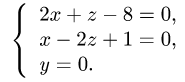
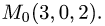
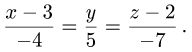
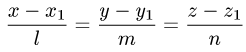
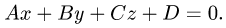
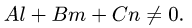
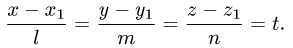
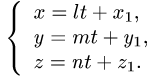
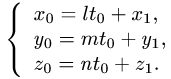
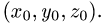
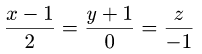
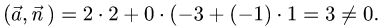
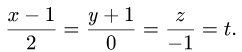
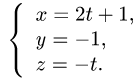
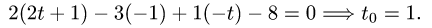
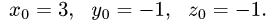
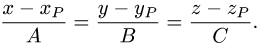
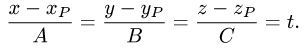
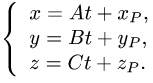
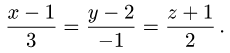
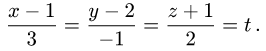
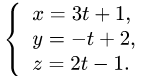
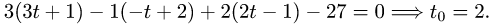
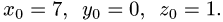
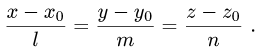
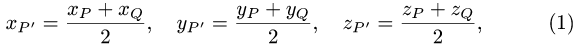
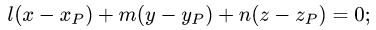
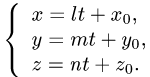
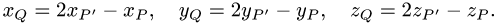
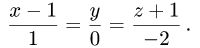
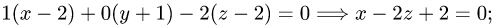
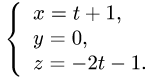
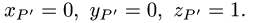
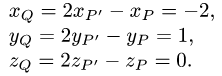
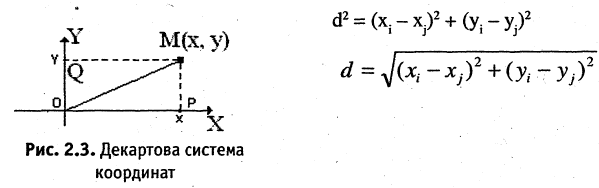
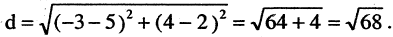
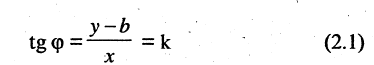
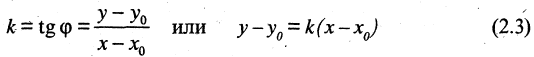
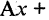
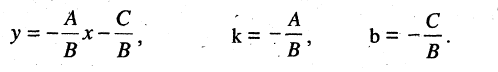
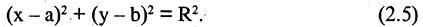
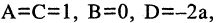
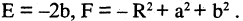
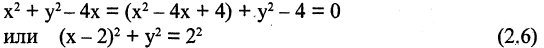
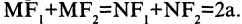
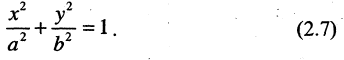

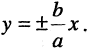

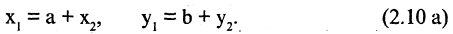
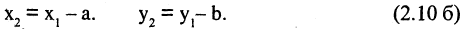
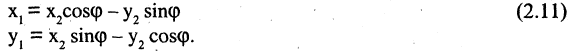

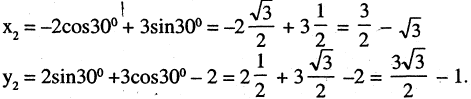
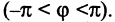

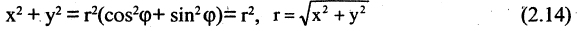
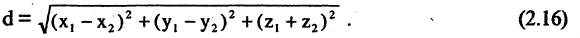
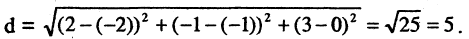

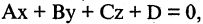 которое описывает плоскость в пространстве. Если
которое описывает плоскость в пространстве. Если 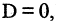 то уравнение
то уравнение 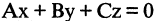 описывает плоскость, проходящую через начало координат (см. главу 2.4).
описывает плоскость, проходящую через начало координат (см. главу 2.4).