Одним из примеров экономического процесса, приводящего к понятию собственного числа и собственного вектора матрицы, является процесс взаимных закупок товаров. Будем полагать, что бюджеты П стран, которые мы обозначим соответственно X1, X2, … , Xn расходуются на покупку товаров. Мы будем рассматривать Линейную модель обмена, или, как ее еще называют, Модель международной торговли.
Пусть Aij — доля бюджета Xj, которую J-я страна тратит на закупку товаров у I-й страны. Введем матрицу коэффициентов Aij:
Тогда если весь бюджет расходуется только на закупки внутри страны и вне ее (можно это трактовать как торговый бюджет), то справедливо равенство
Матрица (16.12) со свойством (16.13), в силу которого сумма элементов ее любого столбца равна единице, называется Структурной матрицей торговли. Для I-й страны общая выручка от внутренней и внешней торговли выражается формулой
Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны ее бюджет должен быть не больше выручки от торговли, т. е. Pi ≥ Xi:, или
Докажем, что в условиях (16.14) не может быть знака неравенства. Действительно, сложим все эти неравенства при I От 1 до N. Группируя слагаемые с величинами бюджетов Xj, Получаем
Нетрудно видеть, что в скобках стоят суммы элементов матрицы А по ее столбцам от первого до последнего, которые равны единице по условию (16.13). Стало быть, мы получили неравенство
Откуда возможен только знак равенства.
Таким образом, условия (16.14) принимают вид равенств:
Введем вектор бюджетов 
, каждая компонента которого характеризует бюджет соответствующей страны; тогда систему уравнений (16.15) можно записать в матричной форме
Это уравнение означает, что собственный вектор структурной матрицы А, отвечающий ее собственному значению λ = 1, состоит из бюджетов стран бездефицитной международной торговли.
Перепишем уравнение (16.16) в виде, позволяющем определить :
Пример. Структурная матрица торговли четырех стран имеет вид:
Найти бюджеты этих стран, удовлетворяющие сбалансированной бездефицитной торговле при условии, что сумма бюджетов задана:
Решение. Необходимо найти собственный вектор , отвечающий собственному значению λ = 1 заданной структурной матрицы А, т. е. решить уравнение (16.17), которое в нашем случае имеет вид
Поскольку ранг этой системы равен трем, то одна из неизвестных является свободной переменной и остальные выражаются через нее. Решая систему методом Гаусса, находим компоненты собственного вектора :
Подставив найденные значения в заданную сумму бюджетов, найдем величину С: С = 1210, откуда окончательно получаем искомые величины бюджетов стран при бездефицитной торговле (в условных денежных единицах):
Найти вектор национальных доходов
Задачи для самостоятельной работы
1. В таблице приведены данные об исполнении баланса за отчетный период, усл. ден. ед.:
Вычислить необходимый объем валового выпуска каждой отрасли, если конечный продукт первой отрасли должен увеличиться в 2 раза, а второй отрасли — на 20%.
2. Структурная матрица торговли трех стран имеет вид
.
Найти соотношение национальных доходов рассматриваемых стран для сбалансированной торговли.
3. Фирмой было выделено 236 тыс. усл. ед. на покупку 29 предметов для оборудования офиса: компьютеров по цене 20 тыс. усл. ед., офисных столов по 8,5 тыс. усл. ед. за стол, стульев по 1,5 тыс. усл. ед. за стул. Другой магазин продавал компьютеры по 19,5 тыс. усл. ед., столы — по
8 тыс. усл. ед., а стулья по той же цене, что и первый магазин. Фирма во втором магазине на ту же самую сумму купила на 1 стол больше. Какое количество единиц каждого вида оборудования было приобретено?
4. Найти равновесный вектор национальных доходов в модели международной торговли для структурной матрицы торговли А , если суммарный доход этих стран составляет 402 усл. ден. ед.:
.
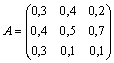
5. Производство состоит из цехов, суммарная прибыль которых в прошедшем году составила 12 млн. усл. ед. На этот год запланировано увеличение прибыли первого цеха на 70%, второго — на 40%. В результате суммарная прибыль должна вырасти в 1,5 раза. Какова величина прибыли каждого цеха в прошлом году?
6. Выяснить, в каком соотношении должны быть национальные доходы трех стран для сбалансированной торговли, если задана структурная матрица торговли А :
.
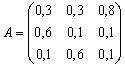
7. Швейная фабрика в течение трех дней производила костюмы, платья, ветровки. Объемы выпуска продукции за три дня и денежные затраты на производство за эти дни представлены в таблице:
Линейная модель обмена
В качестве примера математической модели экономического процесса, приводящейся к понятию собственного вектора и собственного значения матрицы, рассмотрим линейную модель обмена (модель международной торговли).
Пусть имеется п стран Sl,S2 . Sn, национальный доход каждой из которых равен соответственно х1 ,х2 . хп . Обозначим коэффициентами долю национального дохода, которую страна S.- тратит на покупку товаров у страны 5,-. Будем считать, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.
Рассмотрим матрицу А = ^ 21 ^ 22 а2п ,
которая получила название структурной матрицы торговли. В соответствии с (3.32) сумма элементов любого столбца матрицы А равна 1.
Для любой страны S, (/ = 1, 2. п) выручка от внутренней и внешней торговли составит:
Для сбалансированной торговли необходима бездефицитность торговли каждой страны S,, т.е. выручка от торговли каждой страны должна быть не меньше ее национального дохода:
Если считать, что /?, > х,- (i = 1, 2. п), то получаем систему неравенств
Учитывая (3.32), выражения в скобках равны единице, и мы приходим к противоречивому неравенству
Таким образом, неравенство pt >х,- (/ = 1, 2. п) невозможно, и условие Pi^Xj принимает вид Pi=Xi (i = 1, 2. п). (С экономической точки зрения это понятно, так как все страны не могут одновременно получать прибыль.)
Вводя вектор х = <х, х2, хп) национальных доходов стран,
получим матричное уравнение
В котором вектор л: записан в виде вектор-столбца, т.е. задача свелась к отысканию собственного вектора матрицы А, отвечающего собственному значению X = 1.
[> Пример 3.13. Структурная матрица торговли трех стран SlfS2 ,S3 имеет вид:
Найти соотношение национальных доходов стран для сбалансированной торговли.
Решение. Находим собственный вектор х, отвечающий собственному значению X = 1, решив уравнение (А — Е)х = О или систему
Полученный результат означает, что сбалансированность торговли трех стран достигается при векторе национальных доходов
х = ^с; 2с; с j, т.е. при соотношении национальных доходов стран 3/2 : 2 : 1 или 3 : 4 : 2. ?