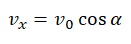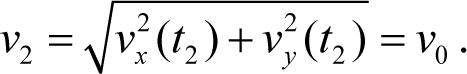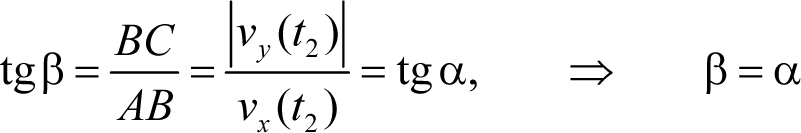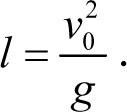Найти угол между вектором скорости и горизонтом (6 видео)

Движение тела, брошенного под углом к горизонту

Содержание

теория по физике 🧲 кинематика
Кинематические характеристики
Тело, брошенное под углом к горизонту с некоторой высоты
Найти угол между вектором скорости и горизонтом
ГЛАВА 5. ДВИЖЕНИЕ ПОД УГЛОМ К ГОРИЗОНТУ
📸 Видео

теория по физике 🧲 кинематика

Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.

Важные факты! График движения тела, брошенного под углом к горизонту:

α — угол, под которым было брошено тело

Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v_0x = v₀cosα. Ее проекция на ось ОУ равна v_0y = v₀sinα.
Проекция мгновенной скорости на ось ОХ равна: v_x = v₀ cosα. Ее проекция на ось ОУ равна нулю: v_y = v₀ sinα – gt.
Проекция ускорения свободного падения на ось ОХ равна нулю: g_x = 0. Ее проекция на ось ОУ равна –g: g_y = –g.

Видео:Угол между векторами. 9 класс.Скачать

Кинематические характеристики

Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:

Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:

Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:

Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: v_y = 0. Время подъема определяется следующей формулой:

Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:

Подставляя в выражение формулу полного времени полета, получаем:

Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:

Учитывая, что x₀ = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v₀ cosα, данная формула принимает вид:

Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:

Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v₀ sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:

Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:

Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?

Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:

Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:

Видео:Угол между векторами | МатематикаСкачать

Тело, брошенное под углом к горизонту с некоторой высоты

Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.

График движения тела, брошенного под углом к горизонту с некоторой высоты:

Время падения тела больше времени его подъема: t_пад > t_под.

Полное время полета равно:

Уравнение координаты x:

Уравнение координаты y:

Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.

Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:

x = v₀ cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.

Алгоритм решения

Решение

Запишем исходные данные:

Построим чертеж и укажем на нем все необходимое:

Нулевой уровень — точка D.

Закон сохранения энергии:

Потенциальная энергия шарика в точке А равна:

Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.

В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:

Перед ударом кинетическая энергия шарика равна:

Согласно закону сохранения энергии:

E p A = E p B + E k B

m g H = m g l 1 + m v 2 2 . .

Отсюда высота H равна:

H = m g l 1 m g . . + m v 2 2 m g . . = l 1 + v 2 2 g . .

Относительно точки В шарик поднимется на высоту h – l₁. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:

h − l 1 = v 2 sin 2 . β 2 g . . = v 2 sin 2 . ( 90 − 2 α ) o 2 g . .

l 1 = h − v 2 sin 2 . ( 90 − 2 α ) o 2 g . .

Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:

H = l 1 + v 2 2 g . . = h − ( g t ) 2 sin 2 . ( 90 − 2 α ) o 2 g . . + ( g t ) 2 2 g . .

H = h − g t 2 sin 2 . ( 90 − 2 α ) 2 . . + g t 2 2 . . = h − g t 2 2 . . ( sin 2 . ( 90 − 2 α ) o − 1 )

H = 1 , 4 − 10 · 0 , 4 2 2 . . ( sin 2 . ( 90 − 6 0 ) o − 1 )

H = 1 , 4 − 5 · 0 , 16 ( sin 2 . 3 0 o − 1 )

H = 1 , 4 − 0 , 8 ( ( 1 2 . . ) 2 − 1 ) = 1 , 4 − 0 , 8 ( 1 4 . . − 1 )

H = 1 , 4 + 0 , 6 = 2 ( м )

pазбирался: Алиса Никитина | обсудить разбор | оценить

В момент t=0 мячик бросают с начальной скоростью v₀ под углом α к горизонту с балкона высотой h (см. рисунок).

Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).

К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.

Алгоритм решения

Решение

Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.

Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.

Координата x меняется согласно уравнению координаты x:

Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:

Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:

В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.

Формула проекции скорости мячика на ось ОХ:

Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.

Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.

Остается последний вариант — координата y. Уравнение этой координаты имеет вид:

Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.

Теперь записываем установленные соответствия в порядке АБ: 42.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?

Для каждой величины определите соответствующий характер изменения:

увеличивается
уменьшается
не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Сделать чертеж, иллюстрирующий ситуацию.
Записать формулы, определяющие указанные в условии задачи величины.
Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.

Решение

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).

Горизонтальная составляющая скорости шарика определяется формулой:

Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).

Ответом будет следующая последовательность цифр — 33.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Видео:Как находить угол между векторамиСкачать

Найти угол между вектором скорости и горизонтом

Математический маятник представляет собой тяжёлый шарик, подвешенный на нерастяжимой нити длиной 1 м. Этот маятник совершает малые свободные колебания так, что нить всё время находится в одной вертикальной плоскости и отклоняется от вертикали на максимальный угол 3°. Из приведённого ниже списка выберите все правильные утверждения, характеризующих движение маятника.

1) Ускорение шарика всегда направлено вдоль его нити.

2) Ускорение шарика постоянно по модулю.

3) Период колебаний маятника равен примерно 2 с.

4) Угол между вектором скорости шарика и горизонтом не может быть больше 3°.

5) Модуль скорости шарика может быть больше 25 см/с.

1. Неверно. При колебаниях возвращающая сила направлена к положению равновесия. Следовательно, ускорение также направлено к положению равновесия и только в этой точке оно направлено вдоль нити.

2. Неверно. При колебаниях вектор ускорения меняется и по модулю, и по направлению.

3. Верно. Период колебаний математического маятника рассчитывается по формуле

4. Верно. Вектор скорости направлен по касательной к траектории, в крайних точках скорость равна 0. Из соображений геометрии угол между горизонтом и вектором скорости не может быть больше 3°.

5. Неверно. Максимальная скорость определяется формулой

Видео:найти угол между единичными векторамиСкачать

ГЛАВА 5. ДВИЖЕНИЕ ПОД УГЛОМ К ГОРИЗОНТУ

Из второй формулы (5.7) и третьего из уравнений (5.2) найдем величину конечной скорости тела v ₂ :

Угол подлета тела к земле – это угол между вектором скорости тела и поверхностью земли. Этот угол можно найти из треугольника, гипотенузой которого является вектор скорости, катетами – его проекции на горизонтальную и вертикальную оси (треугольник АВС , см. рис. 5.2). Имеем

(модуль от проекции v_y ( t ₂) мы взяли потому, что эта проекция отрицательна).

Из полученных соотношений следует, что: (а) полное время движения вдвое больше времени подъема на максимальную высоту (и, следовательно, время подъема равно времени спуска), (б) конечная скорость равна начальной, (в) угол падения равен углу бросания. При этом эти результаты получались «сами» из уравнений движения, то есть их не пришлось предполагать заранее.

Отметим также, что при фиксированной величине начальной скорости дальность полета тела максимальна, если sin 2α = 1 (см. первое из соотношений (5.7)), или α = 45° . При этом сама максимальная дальность полета тела равна

Важной особенностью описания равноускоренного криволинейного движения является возможность представить его как совокупность двух движений: равномерного в направлении, перпендикулярном ускорению, и равноускоренного в направлении ускорения (эту особенность первым понял Г. Галилей). Действительно, уравнения движения, которые получаются в результате проецирования уравнений (5.1) на перпендикулярную и параллельную ускорению оси оказываются такими же, как для равномерно и равноускоренно движущегося тела. Такая возможность позволяет значительно упростить анализ уравнений движения. В качестве примера рассмотрим следующую задачу.