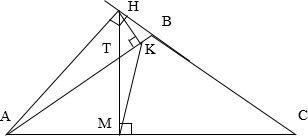
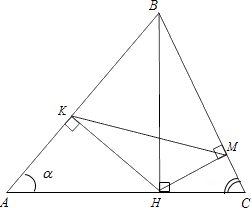
В треугольнике ABC угол ABC тупой, H — точка пересечения продолжений высот, угол AHC равен 60°.
а) Докажите, что угол ABC равен 120°.
б) Найдите BH, если
а) Рассмотрим треугольник AHC. В нем AA1 и CC1 — высоты. Тупой угол между высотами дополняет угол между сторонами, к которым они проведены, до 180°. Поэтому
б) Рассмотрим треугольник AHC, в нем Сторону AC найдём по теореме косинусов:
Тем самым,
Ответ: б)
Докажем утверждение, использованное при решении пункта а).
В четырехугольнике сумма прямых углов
и
равна 180°, поэтому сумма двух других углов
и
также равна 180°. Тогда
Углы
и ABC равны как вертикальные, поэтому
Таким образом, тупой угол между высотами дополняет угол между сторонами, к которым они проведены, до 180°.
Сформулируем теорему, которую мы применили для решения пункта б).
Расстояние от вершины треугольника до точки пересечения его высот равно произведению стороны, противолежащей этой вершине, на котангенс угла при этой вершине. Действительно, пусть высоты AA1, BB1, CC1 треугольника ABC пересекаются в точке H. Стороны прямоугольных треугольников АСС1 и ВНС1 взаимно перпендикулярны, а потому их острые углы АСС1 и ВНС1 равны. Следовательно, эти треугольники подобны. Тогда откуда
Для остроугольного треугольника доказательство аналогично. Для прямоугольного треугольника доказательство напрямую следует из определения котангенса.
Рекомендуем сравнить эту задачу с заданием 505425 из экзаменационного варианта ЕГЭ 2014 года.
Приведем другое решение пункта б):
Рассмотрим треугольник C1CH, заметим, что угол C1CH равен 30°. Поэтому в прямоугольном треугольнике CBA1 катет BA1 вдвое меньше гипотенузы: BA1 = 4. Значит, АA1 = 11. Из треугольника AA1H находим Теперь по теореме Пифагора вычисляем:
Приведем ещё одно решение пункта б):
Заметим, что в треугольнике АНС точка В — ортоцентр. В силу свойства ортоцентра откуда получаем:
(это же следует из подобия треугольников
и
).
Из прямоугольного треугольника CBA1 находим катет BA1, противолежащий углу в 30°: BA1 = 4. Из треугольника АВС находим высоту:
Тогда
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
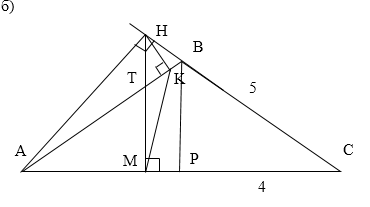
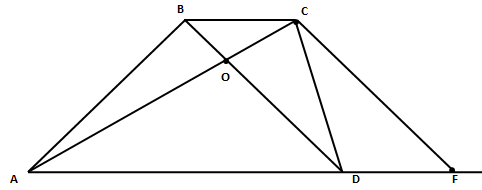
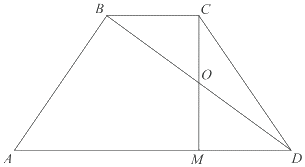
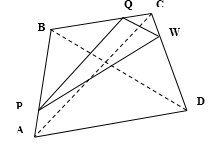
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать  16. ПланиметрияФормат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков. Примеры ответов: 7 или здесьисейчас или 3514 В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно. а) Докажите, что отрезки AM и MK равны. б) Найдите MK, если AB=5, AC=8. Пусть $angle BAC=angle BCA=alpha .$ Тогда $angle ABC=180^-2alpha .$ $angle HBA=180^-180^+2alpha =2alpha $ как смежный с $angle ABC.$ Так как треугольник $AHB$ — прямоугольный, то $angle HAB=90^-2alpha .$ $angle HAC=angle HAB+angle BAC=90^-alpha .$ Так как треугольник $AHM$ — прямоугольный, то $angle AHM=90^-90^+alpha =alpha .$ Аналогично из прямоугольго треугольника $HKB$ получаем, что $angle BHK=90^-2alpha .$ Рассмотрим $angle AHB=90^=angle AHM+angle THK+angle BHK=alpha +angle THK+90^-2alpha Rightarrow angle THK=alpha .$ В треугольниках $ATM$ и $HTK$ $angle TAM=angle THK$ по доказанному, $angle AMT=angle HKT=90^$ по условию. Значит, данные треугольники подобны по призкаку подобия по 2 углам. Следовательно, $displaystyle frac=displaystyle fracRightarrow displaystyle frac=displaystyle frac.$ В треугольнике $ATH$ и $MTK$ $angle ATH=angle MTK$ как вертикальные, $displaystyle frac=displaystyle frac$ по доказанномую Значит, данные треугольники подобны по 2 пропорциональнымсторонам и углу между ними. Тогда, $angle AHT=angle TKM=alpha .$ Получили, что в треугольнике $AKM$ углы при стороне $AK$ равны, значит, треугольник — равнобедренный и $AM=KM.$ Проведем прямую $BP//HM.$ В равнобедренном треугольнике $ABC$ отрезок $BP$ будет являться высотой и медианой, поэтому $PC=4.$ По теорем е Пифагора $BP^=sqrt<BC^-PC^>=3.$ Прямая $BP$ отсекает от треугольника $HCM$ подобные ему треугольник $BCP,$ поэтому $displaystyle frac=displaystyle frac,$ $displaystyle frac=displaystyle fracRightarrow HC=displaystyle fracCM.$ Обозначим $CM=x,$ тогда $HC=displaystyle fracx,$ $BH=displaystyle fracx-5,$ $AM=8-x.$ Из треугольника $ABH$ по теореме Пифагора $AH^=AB^-BH^=25-(displaystyle fracx-5)^=displaystyle fracx-displaystyle fracx^.$ Аналогично из треугольника $AHC$ $AC^=AH^+HC^$ $64=displaystyle fracx-displaystyle fracx^+displaystyle fracx^$ Дана трапеция с диагоналями равными 6 и 8. Сумма оснований равна 10. а) Докажите, что диагонали перпендикулярны. б) Найдите высоту трапеции. а) Проведем прямую CF//BD, тогда BCFD – параллелограмм и BC = DF, CF = BD. В треугольнике ACF AC = 8, CF = 6, AF = AD + DF = 10. Если диагонали перпендикулярны, то треугольник ACF – прямоугольный и выполняется теорема Пифагора: Значит, угол между диагоналями равен 90⁰. б) $S_=displaystyle fraccdot h=5h,$ , где h – длинна высоты. С другой стороны $S_=displaystyle fraccdot BDcdot ACcdot sin 90^=24$ Дана равнобедренная трапеция, в которой AD = 3BC, CM — высота трапеции. а) Доказать, что M делит AD в отношении 2:1. б) Найдите расстояние от точки C до середины BD, если AD = 18, $AC=4sqrt.$. а) Поскольку ABCD — равнобедренная трапеция, то $MD=displaystyle frac=displaystyle frac=BC$ Тогда $AM=2BC$. Следовательно, $displaystyle frac=displaystyle frac$ Треугольник AMC прямоугольный. В нем $AM=displaystyle fracAD=12$ по доказанному в пункте а) и $AC=4sqrt$ по условию. По теореме Пифагора $CM^+AM^=AC^$ , откуда $CM=8$ . Треугольники BCO и MOD равны по катету и острому углу (BC=MD по доказанному в пункте а) , углы CBO и ADO равны как накрест лежащие). Тогда BO = OD и СO = OM как соответственные элементы равных треугольников. Значит, СO — искомое расстояние. В остроугольном треугольнике ABC провели высоту BH из точки H на стороны AB и BC опустили перпендикуляры HK и HM соответственно. а) Докажите, что треугольник MBK подобен треугольнику ABC. б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 2, а радиус окружности, описанной около треугольника ABC равен 4. а) Обозначим $angle BAC=alpha .$. Треугольники AKH, CMH, ABH и BKH – прямоугольные. Тогда $angle KHA=angle ABH=90^-alpha .$. Аналогично $angle KHB=90^-(90^-alpha )=alpha .$. В четырехугольнике BKHM $angle BKH+angle BMH=90^+90^=180^,$, значит, вокруг этого четырехугольника можно описать окружность. Углы $angle KHB=angle KMB=alpha $ как опирающиеся на одну и ту же хорду. В треугольниках ABC и MKB $angle KMB=angle BAC,angle ABC$ — совпадающий. Значит, они подобны по признаку подобия по 2 углам. б) Обозначим k – коэффициент подобия треугольников ABC и MKB (k Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB=CQ:QB=CW:WD=1:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ=16, QW=12, угол PWQ — острый. а) Докажите, что треугольник PQW — прямоугольный. б) Найдите площадь четырёхугольника ABCD. а) По теореме синусов из треугольника $PQW:$ $sin angle PWQ=displaystyle frac,sin angle QPW=displaystyle frac.$ Заметим, что $sin ^angle PWQ+sin ^angle QPW=displaystyle frac+displaystyle frac=1.$ $sin ^angle QPW=cos ^angle PWQ,$ $sin angle QPW=cos angle PWQ,$ так как угол $QWP$ — острый. Тогда $angle QPW+angle PWQ=90^$ и треугольник $PQW$ — прямоугольный. б) Треугольник $PBQ$ и $ABC$ подобные по двум стронам и углу между ими ($angle B$ — общий, $displaystyle frac=displaystyle frac=displaystyle frac).$ Значит, $ACparallel PQ$ и $AC=displaystyle fracPQ=20.$ Аналогично, из подобия треугольников $QCW$ и $BCQ$ получаем, что $BDparallel QW$ и $BD=5QN=60$ Угол между прямыми $BD$ и $AC$ равен углу между прямыми $PQ$ и $QW,$ поэтому $S_=displaystyle fracBDcdot ACcdot sin 90^=displaystyle frac60cdot 20=600.$ Видео:7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать  Дан тупоугольный треугольник abc2021-11-23
Следовательно, $angle BACgt180^$. Пусть $OA=R$ — радиус описанной окружности треугольника $ABC$. По теореме синусов Пусть $S$ — площадь треугольника $ABC$, $p$ — полупериметр, $r=O_H$ — радиус вписанной окружности. Тогда 💥 ВидеоЗадача 6 №27350 ЕГЭ по математике. Урок 42Скачать  Задача 6 №27346 ЕГЭ по математике. Урок 39Скачать  №196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать  Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать  Треугольники: остро-, тупо- и прямоугольныеСкачать  Задача 6 №27345 ЕГЭ по математике. Урок 38Скачать  Высота, биссектриса, медиана. 7 класс.Скачать  Задача 16 из досрочного ЕГЭСкачать  №103. Начертите треугольник ABC с тремя острыми углами и треугольник MNP, у которого угол М тупой.Скачать  Построение медианы в треугольникеСкачать  Построение высоты в треугольникеСкачать  Решаем геометрию ОГЭ по математике 2024! Задание №15.Скачать  7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать  Высота медиана биссектриса в тупоугольном треугольникеСкачать  Построение биссектрисы в треугольникеСкачать  В тупоугольном треугольнике все углы тупые. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать  №1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать  32. Остроугольный, прямоугольный и тупоугольный треугольникиСкачать  |