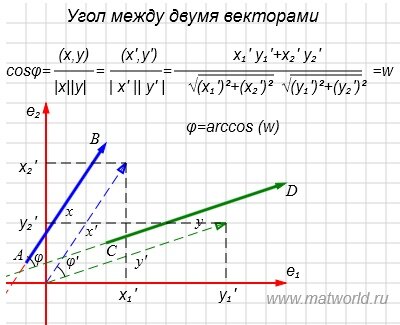
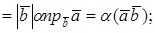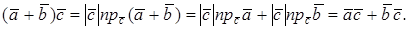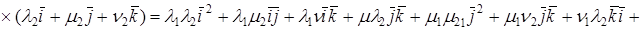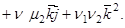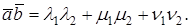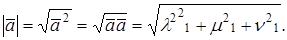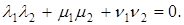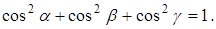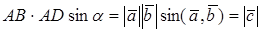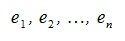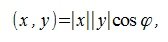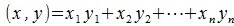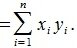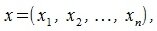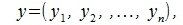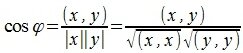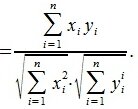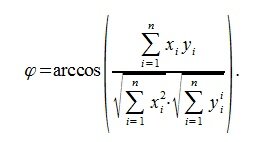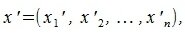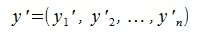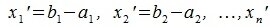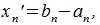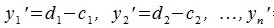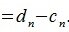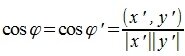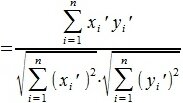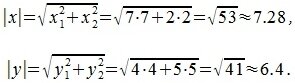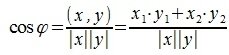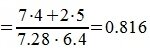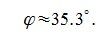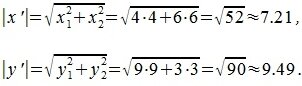Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70
Ответ: a → , b → ^ = — a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,
b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Видео:Угол между векторами | МатематикаСкачать

УГОЛ МЕЖДУ ВЕКТОРАМИ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
ДОКАЗАТЕЛЬСТВО СВОЙСТВ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
Свойство первое следует из определения скалярного произведения: 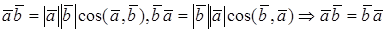
Второе и третье свойства следуют из линейных свойств проекции вектора на ось (направление): 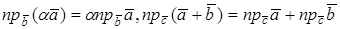
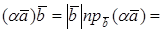
СКАЛЯРНЫЙ КВАДРАТ
Скалярным квадратом называется скалярное произведение 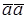
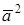
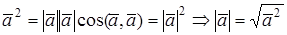
УГОЛ МЕЖДУ ВЕКТОРАМИ
Из определения 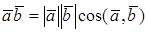
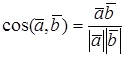
УСЛОВИЕ ОРТОГОНАЛЬНОСТИ ДВУХ ВЕКТОРОВ
Теорема. Векторы 

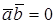
Доказательство необходимости. Пусть 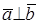
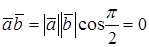

Доказательство достаточности. Пусть 
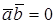
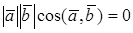
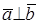
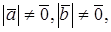
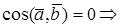
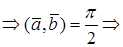
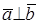
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
Теорема. В ортонормированном базисе скалярное произведение векторов 

Доказательство. Пусть в пространстве выбран ортонормированный базис 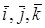


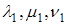

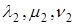
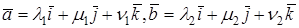
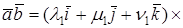
Так как 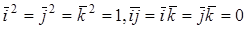
МОДУЛЬ ВЕКТОРА В ОРТОНОРМИРОВАННОМ БАЗИСЕ
Из формулы для скалярного произведения при 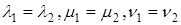
УГОЛ МЕЖДУ ВЕКТОРАМИ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
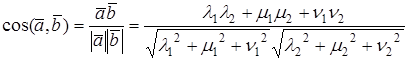
УСЛОВИЕ ОРТОГОНАЛЬНОСТИ ДВУХ ВЕКТОРОВ В
Если 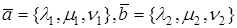
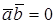
НАПРАВЛЯЮЩИЕ КОСИНУСЫ ВЕКТОРА
Определение. Направляющими косинусами вектора 

Пусть 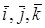
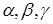

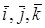
Направляющими косинусами вектора 

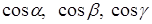
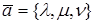
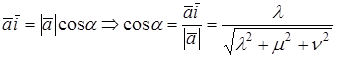
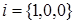
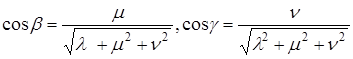
Замечание. Для любого вектора 
ЛИНЕЙНЫЕ СВОЙСТВА ПРОЕКЦИИ ВЕКТОРА НА ОСЬ
В ортонормированном базисе координаты вектора равны проекциям этого вектора на направления соответствующих базисных векторов.
Действительно, если 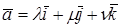
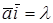
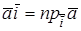
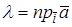
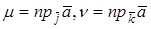
Если 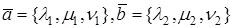
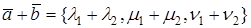
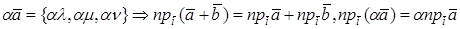
1. Дайте определение скалярного произведения векторов.
2. Выведите условие ортогональности двух векторов.
3. Докажите формулу скалярного произведения векторов в ортогональном базисе.
4. Напишите формулу модуля вектора в ортонормированном базисе.
5. Выведите условие ортогональности двух векторов в ортогональном базисе.
§6. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Векторным произведением вектора 

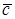
1. 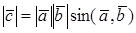
2. 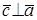
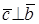
3. Упорядоченная тройка векторов 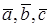
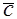
Векторное произведение 

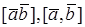
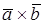
 D C D C 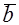 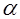 A A  B Рис. 15. B Рис. 15. |     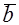 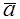  Рис. 14. Рис. 14. |
Замечания. 1. Модуль 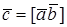


Векторы 

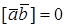
СВОЙСТВА ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
1. 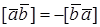
2. 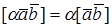
3. 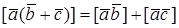
Это свойство примем без доказательства.
ДОКАЗАТЕЛЬСТВО СВОЙСТВ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
1. Пусть 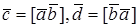
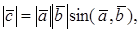
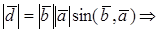
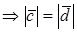
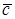
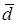


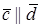
По определению с конца вектора 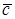


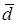


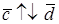
Следовательно, имеем, что 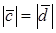
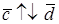
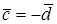
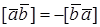
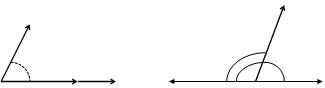   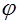 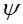 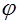 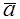 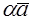 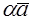 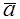 Рис. 16. Рис. 16. |
2. Пусть 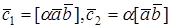
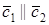
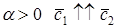
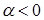
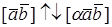
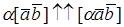
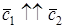
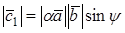
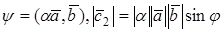
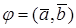
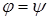
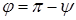
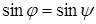
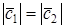
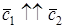
Видео:Угол между векторами. 9 класс.Скачать

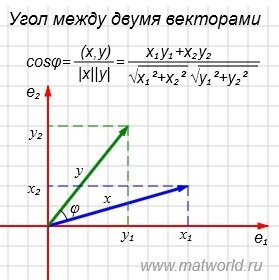
Угол между двумя векторами
Пусть в n-мерном пространстве задан ортонормированный базис
Как известно скалярное произведение ненулевых векторов x и y называется произведение
Если x=0 или y=0, то скалярное произведение равно нулю.
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Так как рассматривается пространство с ортонормированным базисом, то скалярное произведение можно вычислить также из выражения
координаты векторов x и y соответственно.
Из выражений (1) и (2) следует, что косинус угла между двумя векторами равен
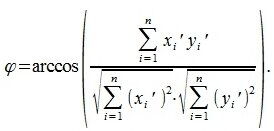
И, следовательно, угол между двумя векторами будет равен
Вариант 2. Начальные точки векторов произвольные.
Пусть заданы векторы x= AB и y= CD, где 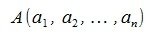
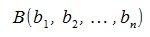
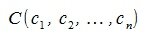
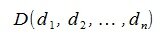
Переместим параллельно векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками):
При таком перемещении угол между векторами x и y равен углу между векторами x’ и y’. Следовательно косинус угла между двумя векторами равен:
Угол между двумя векторами будет равен:
Видео:Нахождение угла между векторами через координаты. 9 класс.Скачать

Примеры вычисления угла между двумя векторами
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Пример . Найти угол между векторами x=(7,2) и y=(4,5).
На рисунке Рис. 1 в двухмерном пространстве представлены векторы x=(7,2) и y=(4,5).
Для вычисления угла между векторами x и y, вычислим нормы векторов x и y:
Косинус угла между векторами x и y, будет равен:
Из выражения (5) вычисляем угол φ:
Вариант 2. Начальные точки векторов произвольные.
Пример . Найти угол между векторами x= AB и y= CD, где A(-1,1), B(3, 7), C(3,2), D(12,5).
На рисунке Рис. 2 в двухмерном пространстве представлены векторы x= AB и y= CD.
Переместим параллельно векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками): x’=(3-(-1),7-1)=(4,6), y’=(12-3,5-2)=(9,3).
Угол φ между векторами x и y равен углу φ’ между векторами x’ и y’. Поэтому вычисляя угол φ’ , получим угол между векторами x и y.
Вычислим норму векторов x’ и y’:
Косинус угла между векторами x’ и y’:
💡 Видео
Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Вывод формулы скалярного произведения векторов, заданных координатами в ортонормированном базисе.Скачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Как находить угол между векторамиСкачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Геометрия 9 класс (Урок№18 - Угол между векторами. Скалярное произведение векторов.)Скачать

11 класс, 5 урок, Угол между векторамиСкачать

найти угол между единичными векторамиСкачать

Косинус угла между векторами. Коллинеарность векторовСкачать

105. Угол между векторамиСкачать

Как разложить вектор по базису - bezbotvyСкачать

Скалярное произведение векторов. 9 класс.Скачать

§48 Ортонормированный базис евклидова пространстваСкачать

100 тренировочных задач #135 Угол между векторамиСкачать

Угол между векторамиСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать