Боковое ребро правильного треугольника

Условие

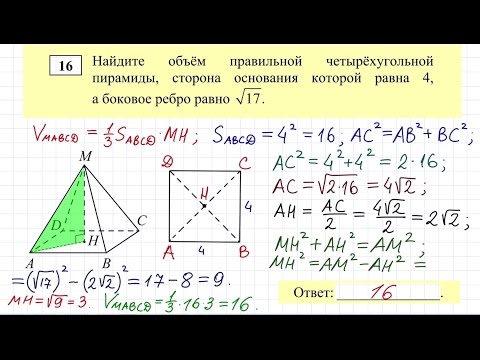
Боковое ребро правильной треугольной пирамиды равно 6см , и составляет с плоскостью основания 60 градусов. Найдите объем пирамиды.
Можно, пожалуйста, с подробным решением, оформлением и рисунком.

Все решения

Δ АВС — равносторонний.
Вершина пирамиды проектируется в точку О.
О- центр вписанной и описанной окружности.

В прямоугольном треугольнике MOA
OA=MA/2=3
катет против угла в 30 градусов равен половине гипотенузы.

По теореме Пифагора
MO^2=MA^2-OA^2=6^2 -3^2=27
MO=3sqrt(3)

Пусть сторона треугольника АВС равна a.
R=asqrt(3)/3 — выражение радиуса описанной около правильного треугольника через сторону.

S_( Δ ABC)=(1/2)a*a*sin60^(o)=a^2sqrt(3)/4

При найденном значении а=3sqrt(3)
S_( Δ ABC)=27*sqrt(3)/4

=(1/3)*(27*sqrt(3)/4) * 3sqrt(3)=81/4

Видео:Самый сложный пример 5 задание проф. ЕГЭ (часть III)Скачать

Боковое ребро правильной треугольной пирамиды равно 6см , и составляет с плоскостью основания 60 градусов?

Геометрия | 10 — 11 классы

Боковое ребро правильной треугольной пирамиды равно 6см , и составляет с плоскостью основания 60 градусов.

Найдите объем пирамиды?

Боковое ребро правильной треугольной пирамиды равно 6см , и составляет с плоскостью основания 60 градусов.

Найдите объем пирамиды.

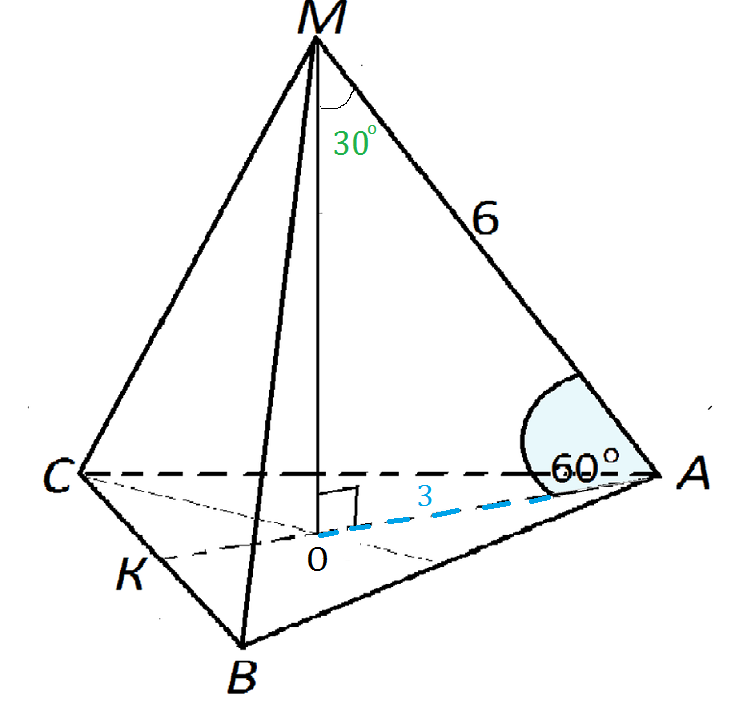
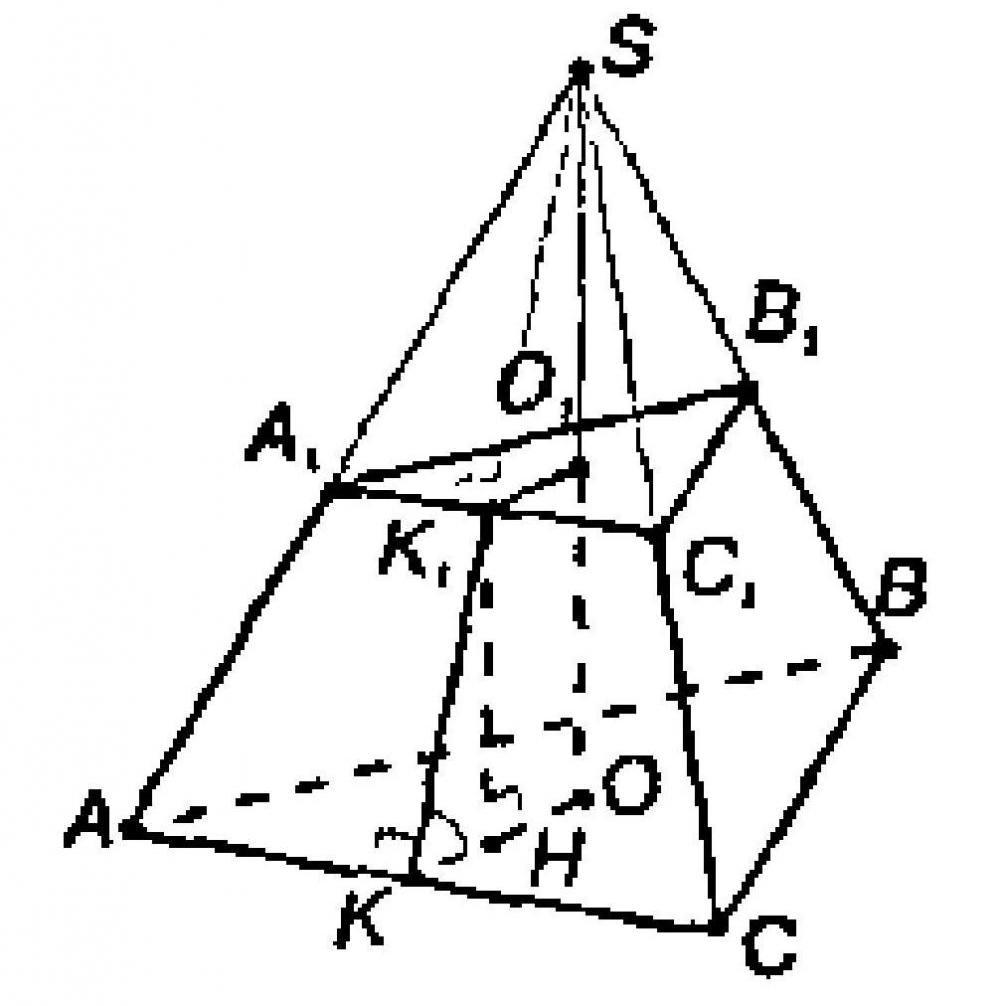
Пусть дана пирамида МАВС,

АК — высота основания.

Площадь равностороннего треугольника (основания), выраженная через высоту, равна

АН противолежит углу 30°и равна 6 : 2 = 3 cм

АН = 2 / 3 высоты основания АК.

Высота основания АК = АН : 2 * 3 = 4, 5 см

S = (4, 5)² : √3 = 6, 75 * √3 см²

V = (6, 75 * √3 * 3√3) : 3 = 20, 25 см³.

Видео:В правильной треугольной пирамиде боковое ребро равно 5Скачать

1)Боковое ребро правильной треугольной пирамиды равно и наклонено к плоскости основания под углом 30°?

1)Боковое ребро правильной треугольной пирамиды равно и наклонено к плоскости основания под углом 30°.

Найдите объем пирамиды.

Видео:Стереометрия Боковое ребро правильной шестиугольной пирамидыСкачать

Найдите косинус угла между боковым ребром и плоскостью основания пирамиды, если все ребра пирамиды равны, а пирамида треугольная?

Найдите косинус угла между боковым ребром и плоскостью основания пирамиды, если все ребра пирамиды равны, а пирамида треугольная.

Видео:№265. В правильной треугольной пирамиде боковое ребро наклонено к плоскости основания под углом 60Скачать

Боковое ребро правильной треугольной пирамиды равно 10 см и составляет с основанием угол 30 градусов?

Боковое ребро правильной треугольной пирамиды равно 10 см и составляет с основанием угол 30 градусов.

Найдите объем пирамиды, Sосн, Sбок, Sполн.

Видео:КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Сторона основания правильной треугольной пирамиды равна 10 см, боковое ребро образует с плоскостью основания угол 60 градусов?

Сторона основания правильной треугольной пирамиды равна 10 см, боковое ребро образует с плоскостью основания угол 60 градусов.

Найти объем пирамиды.

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол в 60 градусов?

Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол в 60 градусов.

Найти объем пирамиды.

Видео:Боковое ребро равно 5, а тангенс угла между боковой гранью и плоскостью основания равен 0,25Скачать

В правильной треугольной пирамиде боковое ребро равно 6 см, угол между боковым ребром и плоскостью основания 60 градусов?

В правильной треугольной пирамиде боковое ребро равно 6 см, угол между боковым ребром и плоскостью основания 60 градусов.

Найдите объем пирамиды.

Видео:Стереометрия, номер 33.1Скачать

Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания 60 градусов?

Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания 60 градусов.

Требуется найти объем пирамиды.

Видео:Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 10. РЕШЕНИЕ!Скачать

Боковые ребра правильной треугольной пирамиды составляют с основанием угол в 60 градусов?

Боковые ребра правильной треугольной пирамиды составляют с основанием угол в 60 градусов.

Найдите объем описанного около пирамиды конуса, если сторона основания пирамиды равна а.

Видео:Откуда берется МАССА у частиц?Скачать

Если можно то поподробнее, боковое ребро правильной треугольной пирамиды равно 6см и составляет с плоскостью основания угол в 60 градусов?

Если можно то поподробнее, боковое ребро правильной треугольной пирамиды равно 6см и составляет с плоскостью основания угол в 60 градусов.

Найти обьем пирамиды.

Видео:Боковые ребра треугольной пирамиды взаимно перпендикулярныСкачать

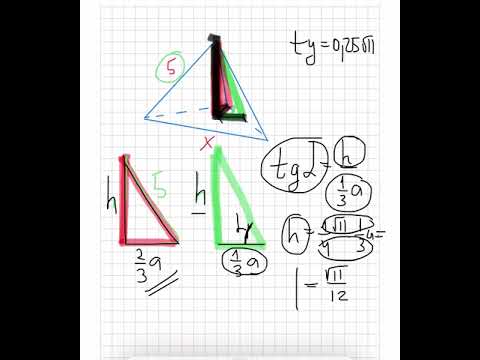
Высота основания правильной треугольной пирамиды составляет три четверти высоты пирамиды?

Высота основания правильной треугольной пирамиды составляет три четверти высоты пирамиды.

Найдите тангенс угла между боковым ребром и плоскостью основания пирамиды.

На этой странице сайта размещен вопрос Боковое ребро правильной треугольной пирамиды равно 6см , и составляет с плоскостью основания 60 градусов? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

Видео:№221. Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 смСкачать

Формулы и свойства правильной треугольной пирамиды. Усеченная треугольная пирамида

Объемной фигурой, которая часто появляется в геометрических задачах, является пирамида. Самая простая из всех фигур этого класса — треугольная. В данной статье разберем подробно основные формулы и свойства правильной пирамиды треугольной.

Видео:Число Бога. Неопровержимое доказательство Бога; The number of God. The incontrovertible proof of GodСкачать

Геометрические представления о фигуре

Прежде чем переходить к рассмотрению свойств правильной пирамиды треугольной, разберемся подробнее, о какой фигуре идет речь.

Предположим, что имеется произвольный треугольник в трехмерном пространстве. Выберем в этом пространстве любую точку, которая в плоскости треугольника не лежит, и соединим ее с тремя вершинами треугольника. Мы получили треугольную пирамиду.

Вам будет интересно: Лихой — это: значение и синонимы

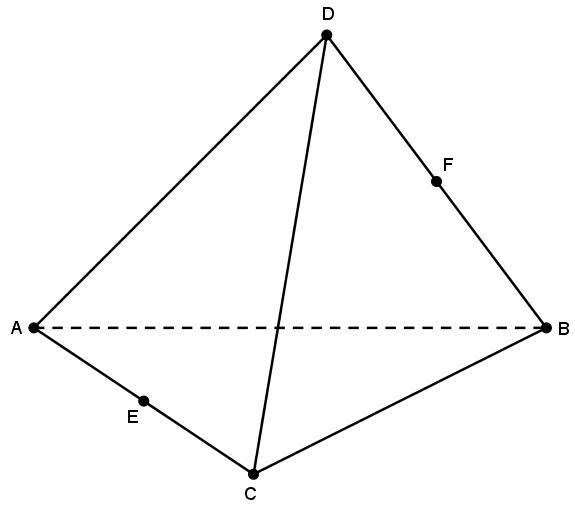
Она состоит из 4-х сторон, причем все они являются треугольниками. Точки, в которых соединяются три грани, называются вершинами. Их у фигуры также четыре. Линии пересечения двух граней — это ребра. Ребер у рассматриваемой пирамиды 6. Рисунок ниже демонстрирует пример этой фигуры.

Поскольку фигура образована четырьмя сторонами, ее также называют тетраэдром.

Видео:Стереометрия, номер 10.1Скачать

Правильная пирамида

Выше была рассмотрена произвольная фигура с треугольным основанием. Теперь предположим, что мы провели перпендикулярный отрезок из вершины пирамиды к ее основанию. Этот отрезок называется высотой. Очевидно, что можно провести 4 разные высоты для фигуры. Если высота пересекает в геометрическом центре треугольное основание, то такая пирамида называется прямой.

Прямая пирамида, основанием которой будет треугольник равносторонний, называется правильной. Для нее все три треугольника, образующих боковую поверхность фигуры, являются равнобедренными и равны друг другу. Частным случаем правильной пирамиды является ситуация, когда все четыре стороны являются равносторонними одинаковыми треугольниками.

Рассмотрим свойства правильной пирамиды треугольной и приведем соответствующие формулы для вычисления ее параметров.

Видео:Найти объем правильной треугольной пирамидыСкачать

Сторона основания, высота, боковое ребро и апотема

Любые два из перечисленных параметров однозначно определяют остальные две характеристики. Приведем формулы, которые связывают названные величины.

Предположим, что сторона основания треугольной пирамиды правильной равна a. Длина ее бокового ребра равна b. Чему будут равны высота правильной пирамиды треугольной и ее апотема.

Для высоты h получаем выражение:

Эта формула следует из теоремы Пифагора для прямоугольного треугольника, сторонами которого являются боковое ребро, высота и 2/3 высоты основания.

Апотемой пирамиды называется высота для любого бокового треугольника. Длина апотемы ab равна:

Из этих формул видно, что какими бы ни были сторона основания пирамиды треугольной правильной и длина ее бокового ребра, апотема всегда будет больше высоты пирамиды.

Представленные две формулы содержат все четыре линейные характеристики рассматриваемой фигуры. Поэтому по известным двум из них можно найти остальные, решая систему из записанных равенств.

Видео:Нахождение бокового ребра правильной пирамидыСкачать

Объем фигуры

Для абсолютно любой пирамиды (в том числе наклонной) значение объема пространства, ограниченного ею, можно определить, зная высоту фигуры и площадь ее основания. Соответствующая формула имеет вид:

Применяя это выражение для рассматриваемой фигуры, получим следующую формулу:

Где высота правильной треугольной пирамиды равна h, а ее сторона основания — a.

Не сложно получить формулу для объема тетраэдра, у которого все стороны равны между собой и представляют равносторонние треугольники. В таком случае объем фигуры определится по формуле:

То есть он определяется длиной стороны a однозначно.

Видео:Угадываем грань кубика вслепую - NumberphileСкачать

Площадь поверхности

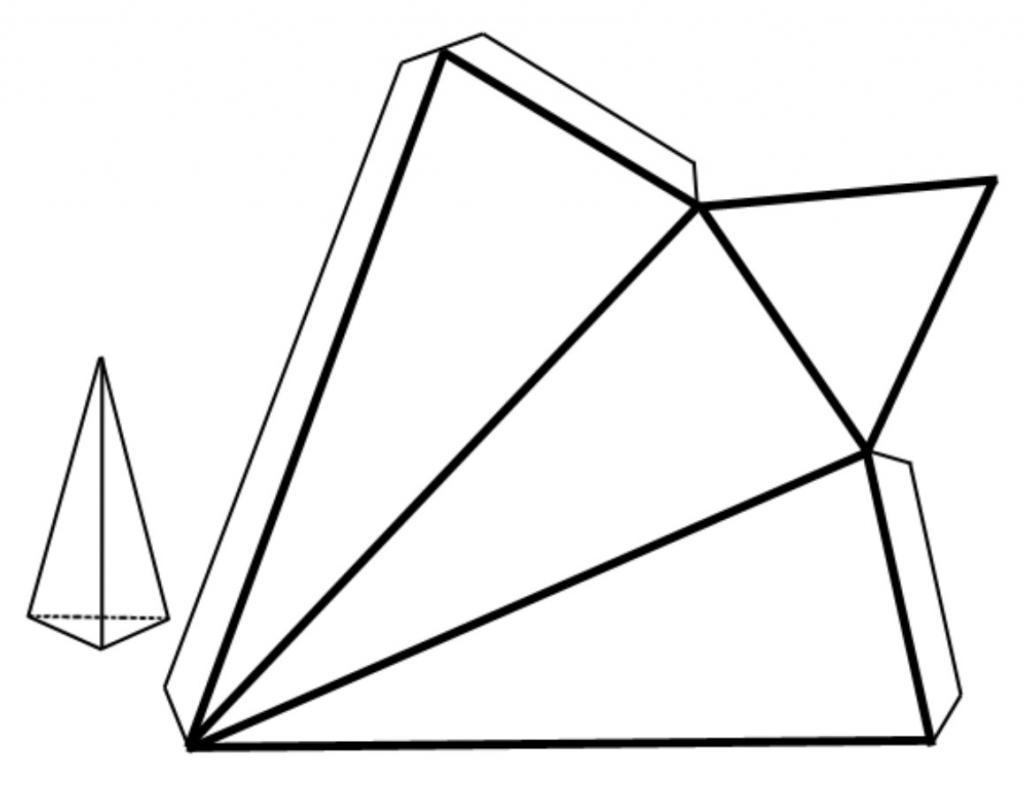
Продолжим рассматривать свойства пирамиды треугольной правильной. Общая площадь всех граней фигуры называется площадью ее поверхности. Последнюю удобно изучать, рассматривая соответствующую развертку. На рисунке ниже показано, как выглядит развертка правильной пирамиды треугольной.

Предположим, что нам известны высота h и сторона основания a фигуры. Тогда площадь ее основания будет равна:

Получить это выражение может каждый школьник, если вспомнит, как находить площадь треугольника, а также учтет, что высота равностороннего треугольника также является биссектрисой и медианой.

Площадь боковой поверхности, образованной тремя одинаковыми равнобедренными треугольниками, составляет:

Данное равенство следует из выражения апотемы пирамиды через высоту и длину основания.

Полная площадь поверхности фигуры равна:

S = So + Sb = √3/4*a2 + 3/2*√(a2/12+h2)*a

Заметим, что для тетраэдра, у которого все четыре стороны являются одинаковыми равносторонними треугольниками, площадь S будет равна:

Видео:Правильная четырехугольная пирамида. Угол между боковой гранью и основанием. Найти ребро основанияСкачать

Свойства правильной усеченной пирамиды треугольной

Если у рассмотренной треугольной пирамиды плоскостью, параллельной основанию, срезать верх, то оставшаяся нижняя часть будет называться усеченной пирамидой.

В случае правильной пирамиды с треугольным основанием в результате описанного метода сечения получается новый треугольник, который также является равносторонним, но имеет меньшую длину стороны, чем сторона основания. Усеченная треугольная пирамида показана ниже.

Мы видим, что эта фигура уже ограничена двумя треугольными основаниями и тремя равнобедренными трапециями.

Предположим, что высота полученной фигуры равна h, длины сторон нижнего и верхнего оснований составляют a1 и a2 соответственно, а апотема (высота трапеции) равна ab. Тогда площадь поверхности усеченной пирамиды можно вычислить по формуле:

S = 3/2*(a1+a2)*ab + √3/4*(a12 + a22)

Здесь первое слагаемое — это площадь боковой поверхности, второе слагаемое — площадь треугольных оснований.

Объем фигуры рассчитывается следующим образом:

V = √3/12*h*(a12 + a22 + a1*a2)

Для однозначного определения характеристик усеченной пирамиды необходимо знать три ее параметра, что демонстрируют приведенные формулы.

🔍 Видео

№258. Боковое ребро правильной четырехугольной пирамиды образует угол в 60° с плоскостью основания.Скачать

Демо-вариант ЕГЭ по математике (базовый уровень) #16-3Скачать