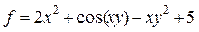Данный пост является продолжением поста Основы работы в Scilab.
Векторы и матрицы представляют собой одномерный и двумерный массивы.
Значение нижней границы индексации элементов массива в Scilab по умолчанию равно единице.
Одномерный массив (вектор-строку) можно задать с помощью команды
где X -название массива, a и b — значения первого и последнего элементов массива, h — шаг, с которым изменяются элементы массива. Возможна запись вида
В этом случае шаг автоматически принимается равным единице. Пример. Задать вектор-строку X с элементами -2,-1,0,1,2.
Пример. Задать вектор-строку X с элементами -2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5, 2.
Другой способ определить вектор — перечислить все его элементы. В этом случае нужно выполнить команду
где X -имя вектора, x1,x2. xn — элементы массива. Пример. Задать вектор-строку X с элементами -5, 0.5, -7, 25.
Для того, чтобы задать вектор-столбец, необходимо перечислить элементы через точку с запятой. Пример. Задать вектор-столбец X с элементами -5, 0.5, -7, 25.
Другой способ задать вектор-столбец — использовать транспонирование матриц. Операция транспонирования задается с помощью знака ‘. Пример.
Для доступа к элементам вектора нужно указать название вектора и в круглых скобках номер элемента. Пример.
Для того, чтобы задать матрицу с элементами xij, нужно выполнить команду вида
Для доступа к элементам нужно указать название матрицы и в круглых скобках номер элемента. Пример.
Матрицы можно формировать на основе имеющихся
С помощью знака «:» можно выполнять различные операции с матрицами Пример.
При работе с матрицами в пакете Scilab можно использовать следующие операции: 1. + — сложение; Пример.
Если к заданной матрице применить некоторую функцию, то элементы матрицы будут преобразованы в соответствии с этой функцией. Пример.
При работе с матрицами можно использовать встроенные функции. Рассмотрим некоторые из них. Функция length(X) возвращает количество элементов матрицы X. Пример.
Функция size(X) возвращает вектор, содержащий количество строк и столбцов матрицы X. Пример.
Функция max(X) возвращает максимальный элемент матрицы X.
Функция min(X) возвращает минимальный элемент матрицы X.
Функция sum(X) возвращает сумму элементов матрицы X.
Функция prod(X) возвращает произведение элементов матрицы X.
Функция det(X) возвращает определитель матрицы X.
Функция inv(X) возвращает матрицу, обратную к X.
Видео:Задача на поиск суммы и произведения элементов спискаСкачать

Найти сумму отрицательных элементов вектора на четных местах scilab
1) Файловая система Scilab и Текущая папка.
2) Встроенный текстовый Редактор SciNotes.
3) Типы программных файлов.
4) Sce-сценарии.
5) Сохранение, вызов и выполнение сценария, сохраненного в sce-файле.
6) Cохранение и восстановление переменных Рабочей области.
7) Числовые выражения и форматирование их результатов.
8) Логические выражения.
9) Простейшие операторы ввода/вывода данных.
1.2.2. Общее задание
1) Изучить материал учебника [1] (п.п. 1.2, 1.5).
2) Выбрать вариант индивидуального задания из табл. 1.2. 3 -1.
3) Выполнить команды clear и clc для очистки окна Обозревателя переменных и Командного окна.
4) Активизировать Редактор SciNotes.
5) Создать sce —сценарий для выполнения индивидуального задания (вычисление выражений) с использованием встроенных в сценарий функций.
6) Сохранить sce —сценарий в sce-файле со смысловым именем .
7) Провести отладку, исправить ошибки и сохранить сценарий.
8) Загрузить sce —сценарий из sce-файла и выполнить его в Командном окне, предварительно присвоив исходным данным допустимые значения.
9) Модернизировать sce-сценарий, вставив в него операторы ввода исходных данных и вывода результата в форматированном виде.
10) Сохранить sce-сценарий под другим именем, исправить ошибки и выполнить.
11) Создать сценарий для решения поставленной задачи и выполнить его.
12) Сохранить все результаты для отчета.
13) Предоставить результаты работы преподавателю, ответить на поставленные вопросы.
14) Оформить отчет по выполненной работе.
Варианты индивидуальных задани й
| № | Задание |
| 1 | 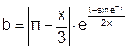 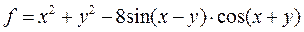 |
| 2 | 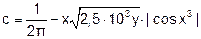 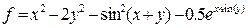 |
| 3 | 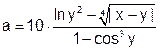 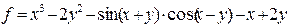 |
| 4 | 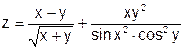 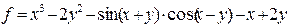 |
| 5 | 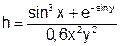 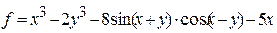 |
| 6 | 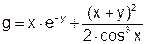 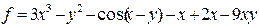 |
| 7 | 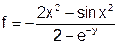 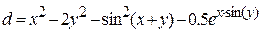 |
| 8 | 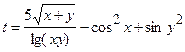 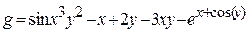 |
| 9 | 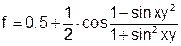 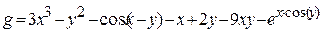 |
| 10 | 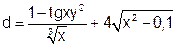 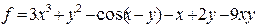 |
| 11 | 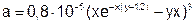 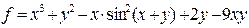 |
| 12 | 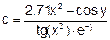 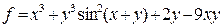 |
| 13 | 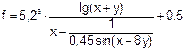 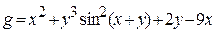 |
| 14 | 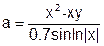 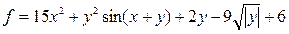 |
| 15 | 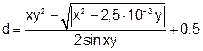 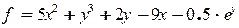 |
| 16 | 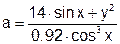 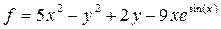 |
| 17 | 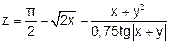 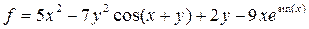 |
| 18 | 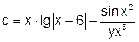 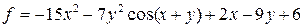 |
| 19 | 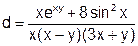 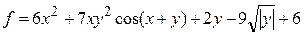 |
| 20 | 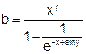 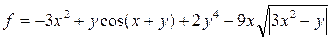 |
| 21 | 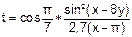 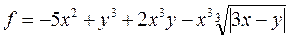 |
| 22 | 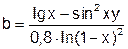 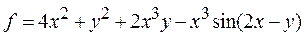 |
| 23 | 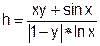 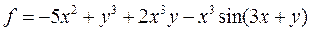 |
| 24 | 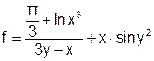 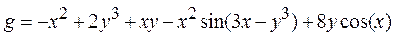 |
| 25 | 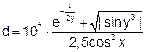 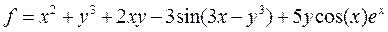 |
| 26 | 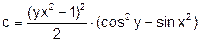 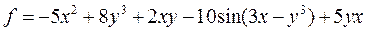 |
| 27 | 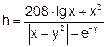 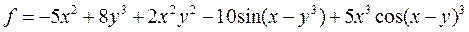 |
| 28 | 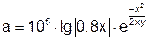 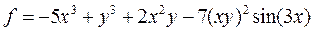 |
| 29 | 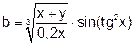 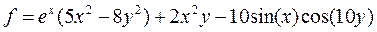 |
| 30 | 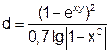 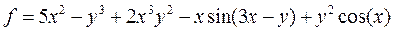 |
Пример выполнения задани я
Пример выполнения задания
1) Решить задачу вычисления арифметических выражений
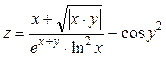
в соответствии с п.п.3-10 общего задания:
2) Результаты выполнения задания (сценарии и протоколы сессии)
//Сценарий Pr 1_2_1. sce вычисления выражений
//Определение функции для вычисления 1-го выражения
//Определение функции для вычисления2-го выражения
function z=f2(x, y)
—>//Протокол сессии Командного окна:
—>// Практическое занятие 1.2 по теме
—>// «Основные объекты системы Scilab»
—>//Присвоение значений,вычисление выражений и вывод результатов
—>// Выполнил:Студент группы БИН1801 Иванов И.И.
—>clear // Очистка окна Обозревателя данных
—>clc // Очистка Командного окна
—>//Загрузка 1-го сценарияPr1_2_1и вызов функций, встроенных в сценарий
—>exec(‘Pr1_2_1.sce’, 0);//Загрузка сценария Pr1_2_1.sceиз текущей папки
—> //Задание начальных значений x и y
—> //Вызов функций f1 и f2, встроенных в сценарий
// Сценарий Pr 1_2_1 mod . sce вычисления выражений
//Определение функции 1-го выражения
//Определение функции 2-го выражения
function z=f2(x, y)
//Ввод исходных данных
//Вычисление значений функций
//Форматирование вывода результата
//Вывод результатов вычисления выражений на экран
—>// Протокол сессии в Командном окне:
—>// Практическое занятие 1.2 по теме
—>// «Основные объекты системы Scilab»
—>// Вариант 0, задание 1 (модифицированное)
—>//Ввод исходных данных, вычисление выражений и вывод результатов
—>// Выполнил: Студент группы БИН1801 Иванов И.И.
—> clear // Очистка окна Обозревателя данных
—> clc // Очистка Командного окна
—>//Загрузка 2-го сценария Pr1_2_1mod
—> exec(‘Pr1_2_1mod.sce’, 0); // Загрузка сценария из текущей папки
Содержание отчета
1) Титульный лист
2) Название и цель практического занятия
3) Общее задание
4) Сценарий, вначале которого должна быть введена информация в виде комментариев:
· имя и назначение сценария;
· вариант индивидуального задания и номер задания.
5) Протокол сессии Командного окна, вначале которого должна быть введена информация в виде комментариев:
· название практического занятия;
· вариант индивидуального задания и номер задания;
· ФИО студента, номер группы;
· краткое перечисление действий, выполняемых во время сессии.
1.2.6. Контрольные вопросы по теме
1) Каким образом открыть новое окно редактора SciNotes?
2) Как в окне Обозреватель файлов сделать нужный каталог текущим?
3) Каким образом открыть в SciNotes ранее созданный файл?
4) Что такое сценарий?
5) Имеет ли сценарий параметры?
6) Допускается ли в SciNotes при вводе текущей строки сценария вернуться к редактированию в предыдущих строках?
7) Какова последовательность действий при сохранении нового сценарий в sce-файле?
8) Каким образом сохранить исправленный текст sce-сценария?
9) Как в редакторе SciNotes осуществляется переход между открытыми окнами, содержащими разные сценарии?
10) Можно ли из одного сценария обращаться к другому?
11) Какой командой, файл, созданный в редакторе SciNotes загрузить в оперативную память?
12) Каким образом в команде exec указывается путь к загружаемому файлу со сценарием?
13) Как и где можно установить текущую папку?
14) Что такое глобальные переменные и когда они используются?
15) Если переменная создана в Командном окне, является ли она видимой для загруженного сценария?
16) Какие переменные являются локальными?
17) Формат оператора ввода данных input?
18) Формат оператора ввода данных x _ dialog?
19) Как с использованием оператора disp осуществить вывод значения переменной или текста можно?
20) Как осуществить вывод результатов вычисления в форматированном виде?
21) Можно ли выполнить сценарий из редактора SciNotes?
1.3 Практическое занятие по теме
« Матри чные операции создания, доступа,
извлечения и модификации »
Цель работы: Изучение способов создания векторов и матриц, операций индексирования, поэлементных выражений с векторами и матрицами.
Вопросы, подлежащие изучению
1) Создание векторов и матриц различного типа.
2) Индексация матриц: векторная, матричная и линейная.
3) Доступ к элементам вектора и матрицы.
4) Матричные операции: арифметических, логических и операций отношения.
5) Функции обработки элементов матриц.
6) Матричная и логическая индексация матриц.
1.3.2 Общее задание
1) Изучить материал учебника [ 1 ] (п.1.3).
2) Выбрать вариант индивидуального задания из табл.1.3-1. Каждое задание содержит две задачи.
3) Выполнить команды clear и clc для очистки окна Обозревателя переменных и Командного окна.
4) Открыть новое окно редактора SciNotes.
5) Создать для выполнения каждой задачи по два сценария. Первый сценарий должен содержать функции, предназначенные для выполнений действий над векторами и матрицами с использованием матричных операций. Второй сценарий предназначен для ввода исходных данных, вызова первого сценария и вывода результатов. Здесь для вывода отдельных значений и пояснений следует использовать функцию mprintf, а для вывода числовых массивов – функции mprintf или disp.
6) Сохранить sce —сценарии в файлах, исправить ошибки.
7) Решить индивидуальные задания, выполнив созданные сценарии.
8) Сохранить все результаты для отчета.
9) Предоставить результаты работы преподавателю, ответить на поставленные вопросы.
10) Оформить отчет по выполненной работе.
Варианты индивидуальных заданий
| № | 1-я задача | 2-я задача |
| 1 | Ввести 3 вектора разной длины и найти сумму отрицательных элементов каждого из них. | В матрице А(3х4)определить произведение элементов, расположенных на нечетных местах в каждой строке. Заменить полученными значениями элементы первого столбца матрицы. |
| 2 | Подсчитать количество «единиц» на четных местах введенного вектора. | В матрице Х(4×5)поменять столбец, в котором находится максимальный элемент, с её первым столбцом. |
| 3 | Найти сумму положительных элементов введенного вектора, стоящих на местах, кратных числу n. | В матрице T(3×5)определить строки, в которых расположено более двух элементов, равных нулю. Заменить все элементы этих строк на 100. |
| 4 | Найти сумму элементов введенного вектора, стоящих на местах кратных трем и больших заданного числа x. | Элементы каждой строки матрицы, значения которых больше среднеарифметического значения данной строки, заменить этим значением. |
| 5 | Найти сумму отрицательных элементов введенного вектора, расположенных на нечетных местах. | Все отрицательные элементы матрицыС(3х4) умножить на х1, а положительные – разделить на х2. Подсчитать количество нулевых элементов. |
| 6 | Найти произведение элементов введенного вектора, больших или равных, введенному значению х. | В введенной матрице Ввсе элементы, модули которых равны модулям максимального или минимального элемента, заменить значением y. |
| 7 | Найти сумму последних n элементов введенного вектора, меньших числа х. | Найти сумму элементов прямоугольной матрицы D, не лежащих в интервале [a,b]. Заменить этим значением все элементы, попавшие в этот интервал. |
| 8 | Среди n первых элементов введенного вектора найти сумму отрицательных элементов. | Элементы квадратной матрицы ниже главной диагонали уменьшить на х1 , а элементы выше главной диагонали увеличить на х2. |
| 9 | Найти сумму и количество элементов введенного вектора, больших числа х. | Найти количество отрицательных элементов в каждой строке квадратной матрицы F(nxn)и заменить полученными значениями элементы главной ее диагонали. |
| 10 | Подсчитать количество элементов введенного вектора, принадлежащих интервалу [a,b]. | В матрице А(4×5)определить столбцы, в которых все одинаковые элементы. Заменить элементы этих столбцов случайными целыми числами от 0 до 100. |
| 11 | Найти первый отрицательный элемент введенного вектора и вывести его номер и значение. | Максимальный элемент каждой строки матрицы D(4,4)заменить числом х. |
| 12 | Найти количество элементов введенного вектора, меньших единицы. | Найти среднегеометрическое значение элементов каждого столбца квадратной матрицы и заменить им элементы главной диагонали матрицы Y. |
| 13 | Найти количество нулевых элементов введенного вектора среди его последних n элементов. | В каждой строке матрицы К(m×n) найти количество элементов больше х1и заменить их на значение последнего элемента строки. Вывести полученную матрицу по столбцам. |
| 14 | Найти произведение ненулевых элементов вектора. | Минимальный элемент в каждом из столбцов матрицы заменить нулевым значением. |
| 15 | Найти произведение положительных элементов вектора, расположенных на нечетных местах. | В матрице поменять строку, в которой находится минимальный элемент, с последней строкой. |
| 16 | Определить среднее значение всех отрицательных элементов вектора Р. | В матрице определить строки, в которых не все элементы одинаковы. Увеличить элементы этих строк на значение х. |
| 17 | Найти сумму элементов вектора, не попавших в интервал [a,b]. | В матрице определить сумму отрицательных элементов каждого столбца. Заменить полученными значениями элементы второй строки. |
| 18 | Найти сумму отрицательных элементов вектора на четных местах. | Найти среднее арифметическое значений элементов матрицы A(nxn)и заменить этим значением элементы последней строки и последнего столбца. |
| 19 | Определить сумму положительных и произведение отрицательных элементов вектора. | В матрице определить столбцы, в которых расположено более двух нулевых элементов. Заменить элементы в этих столбцах назначение х. |
| 20 | Определить количество элементов вектора, кратных x. | Элементы каждого столбца матрицы, которые меньше среднеарифметического значения данного столбца, заменить этим значением. |
| 21 | Найти максимальное значение среди элементов вектора между номерами n1 и n2. | В вещественной матрице определить суммы элементов, расположенных на нечетных местах в каждой строке. Заменить полученными значениями элементы последнего столбца матрицы. |
| 21 | Найти общее количество элементов вектора, равных х1и х2. | Максимальные элементы матрицы (их может быть несколько) увеличить на среднее значение всех элементов, расположенных выше главной диагонали. |
| 22 | Найти предпоследний отрицательный элемент введенного вектора Х. | Все элементы матрицы, кратные х, заменить минимальным значением элемента матрицы. |
| 23 | Подсчитать сумму и произведение первых n положительных элементов введенного вектора. | Во введенной матрице заменить все элементы, равные числу х, на среднее значение элементов матрицы. |
| 24 | Определить номер минимального по модулю элемента вектора-столбца. | Найти количество элементов матрицыС(5х5), лежащих в интервале [a,b], и заменить этим значением элементы, лежащие на главной диагонали. |
| 25 | Найти наибольший отрицательный элемент вектора. | Найти произведение положительных элементов главной диагонали квадратной матрицы А. Заменить полученным значением все отрицательные элементы матрицы. |
| 26 | Подсчитать сумму квадратов четных и сумму квадратов нечетных элементов вектора. | В матрице определить произведения элементов, расположенных на четных местах в каждом столбце. Заменить полученными значениями элементы первой строки матрицы. |
| 27 | Вывести значение и номер последнего нечетного отрицательного элемента вектора. | Элементы матрицы уменьшить на минимальное значение её элементов, кратных х. |
| 28 | Определить элемент вектора, наиболее близкий по своему значению к заданному x. | В матрице симметрично поменять между собой элементы выше главной диагонали с элементами ниже главной диагонали, а элементы главной диагонали расположить в обратном порядке. |
| 29 | Определить первый максимальный элемент вектора и заменить его нулем. | Для матрицы А найти среднее арифметическое сумм элементов, расположенных над и под главной диагональю. |
| 30 | В векторе Х поменять местами минимальное и максимальное значения элементов. | Ввести квадратную матрицу и получить из ее элементов другую, каждый элемент которой умножен на значение ее определителя. |
Примеры выполнения задани й
Пример выполнения задания 1
1) В соответствии с п.п.5-7 общего задания решить задачу 1: Среди n последних элементов вектора найти количество элементов, равных вводимому
Видео:Найти сумму направляющих косинусов вектораСкачать

Сумма элементов вектора scilab
Видео:Паскаль с нуля [ч10]. Вывод массива, задача с четными числамиСкачать
![Паскаль с нуля [ч10]. Вывод массива, задача с четными числами](https://i.ytimg.com/vi/a4_jOnRmAmo/0.jpg)
IT Novella
Данный пост является продолжением поста Основы работы в Scilab.
Векторы и матрицы представляют собой одномерный и двумерный массивы.
Значение нижней границы индексации элементов массива в Scilab по умолчанию равно единице.
Одномерный массив (вектор-строку) можно задать с помощью команды
где X -название массива, a и b — значения первого и последнего элементов массива, h — шаг, с которым изменяются элементы массива. Возможна запись вида
В этом случае шаг автоматически принимается равным единице. Пример. Задать вектор-строку X с элементами -2,-1,0,1,2.
Пример. Задать вектор-строку X с элементами -2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5, 2.
Другой способ определить вектор — перечислить все его элементы. В этом случае нужно выполнить команду
где X -имя вектора, x1,x2. xn — элементы массива. Пример. Задать вектор-строку X с элементами -5, 0.5, -7, 25.
Для того, чтобы задать вектор-столбец, необходимо перечислить элементы через точку с запятой. Пример. Задать вектор-столбец X с элементами -5, 0.5, -7, 25.
Другой способ задать вектор-столбец — использовать транспонирование матриц. Операция транспонирования задается с помощью знака ‘. Пример.
Для доступа к элементам вектора нужно указать название вектора и в круглых скобках номер элемента. Пример.
Для того, чтобы задать матрицу с элементами xij, нужно выполнить команду вида
Для доступа к элементам нужно указать название матрицы и в круглых скобках номер элемента. Пример.
Матрицы можно формировать на основе имеющихся
С помощью знака «:» можно выполнять различные операции с матрицами Пример.
При работе с матрицами в пакете Scilab можно использовать следующие операции: 1. + — сложение; Пример.
Если к заданной матрице применить некоторую функцию, то элементы матрицы будут преобразованы в соответствии с этой функцией. Пример.
При работе с матрицами можно использовать встроенные функции. Рассмотрим некоторые из них. Функция length(X) возвращает количество элементов матрицы X. Пример.
Функция size(X) возвращает вектор, содержащий количество строк и столбцов матрицы X. Пример.
Функция max(X) возвращает максимальный элемент матрицы X.
Функция min(X) возвращает минимальный элемент матрицы X.
Функция sum(X) возвращает сумму элементов матрицы X.
Функция prod(X) возвращает произведение элементов матрицы X.
Функция det(X) возвращает определитель матрицы X.
Функция inv(X) возвращает матрицу, обратную к X.
Видео:Бинарный поиск по ответу: задачи «Дипломы» и «Коровы — в стойла»Скачать

Обработка структурированных данных в Scilab
Краткие теоретические сведения
В Scilab можно использовать различные типы структурированных данных, т.е. данных, содержащих несколько элементов. К основным структурированным данным относятся массивы чисел (вектора, матрицы, многомерные массивы).
Массив — это последовательность однотипных элементов, снабженных индексами (порядковыми номерами). Вектором принято называть одномерный массив. Матрица — это двумерный массив. Векторы в Scilab делятся на векторы-строки и векторы-столбцы.
Занести числа в вектор можно несколькими способами.
1) Непосредственный ввод
Чтобы задать вектор-строку, значения его элементов следует перечислить в квадратных скобках, разделяя пробелами.
Чтобы задать вектор-столбец, значения его элементов следует перечислить в квадратных скобках, используя для разграничения строк точку с запятой.
Обращение к элементу вектора выполняется указанием имени вектора и номера элемента в векторе в круглых скобках.
Например, V(2) à 3
2) Ввод с использованием диапазона
Общий вид диапазона:
xn – начальное значение диапазона;
dx – шаг изменения значений диапазона;
xk – конечное значение диапазона;
Для формирования вектора следует задать:
В результате будет сформирован вектор, первый элемент которого равен xn, второй – xn+dx, третий — xn+dx+dx и т.д. Последний элемент будет не больше xk для положительного шага dx , и не меньше xk – для отрицательного. Если величина шага отсутствует, то по умолчанию его значение равно 1 или -1, тогда вид диапазона таков:
Примеры правильной записи задания вектора с использованием диапазонов приведены ниже.
| Фрагмент программы a=5:2:15 disp(a) v=3:5 disp(v) | Командное окно 5 7 9 11 13 15 3 4 5 |
Задачу о табулировании функции можно решить с помощью формирования векторов X и Y, например:
X=0:0.5:6.28
Y=cos(X)
В этом случае в каждый элемент вектора Y поместится косинус от каждого элемента вектора Х.
Чтобы задать матрицу, значения ее элементов следует перечислить в квадратных скобках, разделяя элементы в строках пробелами или запятыми, а для разграничения строк использовать точку с запятой.
| Фрагмент программы A=[ 3 1 -3; 2 0 1.5] | Командное окно 3. 1. -3. 2. 0 1.5 |
Для указания отдельного элемента матрицы после имени матрицы в круглых скобках указываются два индекса: номер строки и номер столбца.
Например, M(2,3) – это второй по строке и третий по столбцу элемент матрицы M.
Система имеет обширный набор стандартных функций и операций по обработке матриц, который позволяет:
— формировать новые матрицы стандартного вида;
— выполнять матричные арифметические операции;
— вычислять матричные характеристики и математические функции.
Для формирования новых матриц стандартного вида применяются следующие системные функции:
rand(M,N) – формирует прямоугольную матрицу размерностью M×N, элементами которой являются случайные числа в интервале (0.0; 1.0), функция rand без параметров формирует одно случайное число в том же интервале.
ones(M,N) формирует матрицу размерностью M×N, состоящую из единиц.
zeros(M,N) формирует матрицу размерностью M×N, состоящую из нулей.
diag(V) создает диагональную матрицу, в которой элементы вектора V являются элементами главной диагонали.
Матричные арифметические операции представлены следующими:
A+B , A-B матричное сложение и вычитание. Оба операнда этой операции должны иметь одинаковую размерность, если они являются матрицами. Один из операндов может выть скалярной величиной.
A*B матричное умножение. Операция выполняется по правилам матричного умножения, число столбцов матрицы A должно быть равно числу строк матрицы B.
Х ^ Р возведение матрицы в степень. Эта операция при скалярном значении Р возводит квадратную матрицу Х в степень Р. Если Х – скалярная величина, а Р – квадратная матрица, то Х^Р возводит Х в матричную степень Р. Эта операция является ошибочной, если оба операнда – матрицы.
В Scilab существуют матричные операции, которые выполняются над каждым элементом матрицы, это такие операции, как:
.* поэлементное матричное умножение.
.поэлементное левое деление матриц.
. / поэлементное правое деление матриц.
.^поэлементное возведение матрицы в степень.
Оба операнда этих операций должны иметь одинаковую размерность, или один из них должен являться скалярной величиной.
Операция «апостраф» ′ вычисляет транспонированную матрицу.
Ниже приведены примеры выполнения матричных арифметических операций.
| Фрагмент программы умножения двух матриц x=[2 3 4; 5 6 7] y=[9 8; 7 6; 5 4] z=x*y disp(z) | Командное окно 59 50 122 104 |
| Фрагмент программы умножения матрицы на вектор x=[2 3 4; 5 6 7] t=[3; 6; 9] z=x*t disp(z) | Командное окно |
| Поэлементное умножение двух матриц x=[2 3 4; 5 6 7] y=[9 8 7 ; 6 5 4] z=x .*y disp(z) | Командное окно 18 24 28 30 30 28 |
| Вычисление транспонированной матрицы y=[9 8 7 ; 6 5 4] w=y’ disp(w) | Командное окно 9 6 8 5 7 4 |
Система содержит стандартные функции, позволяющие вычислять различные характеристики матриц:
det(A) вычисляет определитель матрицы;
trace(A) вычисление следа матрицы;
rank(A) вычисление ранга матрицы;
inv(A) вычисление обратной матрицы.
Ниже приведены примеры вычисления этих характеристик для матриц А и В.
| Фрагмент программы вычисления определителя матрицы x=[2 3 4; 5 6 7; 1 2 2]; d=det(x) disp(“определитель =”) disp (d) | Командное окно определитель = |
| Фрагмент программы вычисления обратной матрицы x=[2 3 4; 5 6 7; 1 2 2]; Z= inv(x) disp(Z) | Командное окно -0.6667 0.6667 -1. -1. 0 2. 1.3333 -0.3333 -1. |
Над массивами можно выполнять различные операции, заданные системными функциями.
max(А) — вычисление максимального элемента массива;
min(А) — вычисление минимального элемента массива;
sum(A) — вычисление суммы элементов массива;
prod(A) — вычисление произведения элементов массива;
mean(A) — вычисление среднего значения элементов массива.
[Amax, Nmax]= max(A) — вычисление максимального элемента в массиве и его номера. Порядок применения этих функций и результаты их выполнения рассмотрены на примерах.
| Поиск максимального значения матрицы и номера его строки и столбца y=[2 3 4; 55 6 7; 1 12 2]; [ymax,nmax]=max(y) disp(y) disp(ymax) disp(nmax) | Командное окно 2. 3. 4. 55. 6. 7. 1. 12. 2. 55. 2. 1. |
| Фрагмент программы вычисления суммы элементов матрицы x=[2 3 4; 5 6 7; 1 2 2]; s=sum(x), disp(s) | Командное окно |
Практическая часть
Задание 1. Создание нескольких векторов с указанными параметрами
Постановка задачи. Создать вектор х, значения которого изменяются от 22 до 37 с шагом 1.
Создать вектор d, значения которого изменяются от 2 до 7 с шагом 0,5.
Пример программы по выполнению этого задания приведен ниже.
| Программа | Результаты расчетов |
| x=22:37disp(«вектор х»)disp(x)d=2:0.5:7disp(«вектор d»)disp(d) | вектор х 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. вектор d 2. 2.5 3. 3.5 4. 4.5 5. 5.5 6. 6.5 7. |
Индивидуальные задания приведены в таблице 2.2.
| № | Задание |
| Создать вектор х, значения которого изменяются от 22 до 37 с шагом 1. Создать вектор d, значения которого изменяются от 2 до 7 с шагом 0,5. | |
| Создать вектор х, значения которого изменяются от 32 до 43 с шагом 1. Создать вектор y, значения которого изменяются от 12 до 27 с шагом 0,2. | |
| Создать вектор х, значения которого изменяются от 3 до 13 с шагом 1. Создать вектор q, значения которого изменяются от 1,2 до 2,7 с шагом 0,05. | |
| Создать вектор х, значения которого изменяются от 15 до 26 с шагом 1. Создать вектор b, значения которого изменяются от 18,2 до 23,7 с шагом 0,5. | |
| Создать вектор х, значения которого изменяются от 9 до 18 с шагом 1. Создать вектор u, значения которого изменяются от 6,2 до 13,7 с шагом 0,5. | |
| Создать вектор х, значения которого изменяются от 42 до 57 с шагом 1. Создать вектор r, значения которого изменяются от 16,2 до 30,7 с шагом 0,5. | |
| Создать вектор a, значения которого изменяются от 17 до 32 с шагом 1. Создать вектор w, значения которого изменяются от 26,7 до 44,2 с шагом 0,8. | |
| Создать вектор х, значения которого изменяются от 32 до 47 с шагом 1. Создать вектор d, значения которого изменяются от 12 до 17 с шагом 0,5. | |
| Создать вектор х, значения которого изменяются от 23 до 40 с шагом 1. Создать вектор y, значения которого изменяются от 2 до 17 с шагом 1,2. | |
| Создать вектор х, значения которого изменяются от 8 до 23 с шагом 1. Создать вектор q, значения которого изменяются от 13,2 до 22,7 с шагом 0,9. | |
| Создать вектор х, значения которого изменяются от 25 до 36 с шагом 1. Создать вектор b, значения которого изменяются от 8,2 до 13,7 с шагом 0,5. | |
| Создать вектор х, значения которого изменяются от 19 до 38 с шагом 1. Создать вектор u, значения которого изменяются от 16,2 до 23,7 с шагом 0,7. | |
| Создать вектор х, значения которого изменяются от 22 до 37 с шагом 1. Создать вектор r, значения которого изменяются от 26,2 до 43,7 с шагом 0,5. | |
| Создать вектор a, значения которого изменяются от 27 до 39 с шагом 1. Создать вектор w, значения которого изменяются от 22,7 до 40,2 с шагом 0,9. | |
| Создать вектор a, значения которого изменяются от 17 до 41 с шагом 1. Создать вектор w, значения которого изменяются от 16,7 до 34,2 с шагом 0,6. |
Задание 2.Создание одномерного массива как диапазона с заданными пределами изменения
Постановка задачи. Создать одномерный массив как диапазон с заданными пределами изменения. Массив должен содержать не менее 10 чисел. Сформировать новый одномерный массив, содержащий значения функции от элементов исходного массива.
| Функция | хн | хк |
 |
Для выполнения этого задания запрограммируем следующие действия:
Шаг 1. Создадим вектор x, значения которого будут изменяться от 0 до 2 с шагом 0.2 (вектор создается с использованием диапазона).
Шаг 2. Создадим вектор y, каждое значение которого вычисляется с помощью заданной формулы (не забываем про поэлементные операции над векторами).
Шаг 3. Выведем в командное окно числовые значения полученных векторов.
| Программа | Результаты расчетов |
| clearx=0:0.2:2y=(4-x^2).*x^2disp(«вектор x»)disp(x)disp(«вектор y»)disp(y) | вектор x 0. 0.2 0.4 0.6 0.8 1. 1.2 1.4 1.6 1.8 2. вектор y 0. 0.1584 0.6144 1.3104 2.1504 3. 3.6864 3.9984 3.6864 2.4624 0. |
Индивидуальные задания приведены в таблице 2.3.
| № вар. | Функция | X1 | X2 | № вар. | Функция | X1 | X2 |
| 1. |  | 2. |  | ||||
| 3. |  | -3 | 4. |  | -1 | ||
| 5. |  | 6. |  | ||||
| 7. |  | -2 | 8. |  | |||
| 9. |  | 10. |  | ||||
| 11. |  | 12. |  | ||||
| 13. |  | 14. |  | -1 | |||
| 15. |  | 16. |  | -1 |
Задание 3. Обработка матриц и векторов
Постановка задачи. Даны две матрицы А и В.
A=  B= B=  |
1) Создать вектор V1 из второго столбца матрицы А, вектор V2 из третьей строки матрицы В и вектор V3 из первого столбца матрицы B.
Порядок составления программы таков.
Шаг 1. Создаем матрицы перечислением элементов по строкам, разделителем между строками является «;».
Шаг 2. Выводим матрицы в командное окно.
Шаг 3. Формируем вектор V1 из всех строк второго столбца матрицы A, поэтому в качестве номера строки матрицы указываем символ «:», что означает «все», а в качестве номера столбца указываем 2. Аналогично формируются вектора V2 и V3;
Шаг 4. Выводим значения векторов в командное окно.
| Программа | Результаты расчетов |
| A=[2 -1 -3; 8 -7 -6; -3 4 2]B=[2 -1 -2; 3 -5 4; 1 2 1]disp(A)disp(B) | 2. — 1. — 3. 8. — 7. — 6. — 3. 4. 2. 2. — 1. — 2. 3. — 5. 4. 1. 2. 1. |
| V1=A(:,2)V2=B(3,:)V3=B(:,1)disp(V1)disp(V2)disp(V3) | — 1. — 7. 4. 1. 2. 1. 2. 3. 1. |
2) Вычислить V2×V1 и A×V1.
Порядок составления программы таков.
Шаг 1. Выбираем переменные, например, R1 и R2, которые будут являться результатами выполнения операций умножения.
Шаг 2. Так как операции умножения выполняются по законам математики, то точка перед знаком умножения не ставится. Ожидаемый результат умножения двух векторов – одно число, а результат умножения матрицы на вектор – это вектор-столбец из трех элементов.
Шаг 3. Выводим результаты в командную область с помощью оператора disp.
| Программа | Результаты расчетов |
| R1=V2*V1disp(R1)R2=A*V1disp(R2) | — 11. — 7. 17. — 17. |
3) Вычислить A×B, A -1 , B T .
Порядок составления программы таков.
Шаг 1. Выбираем переменные, например, W1, W2, W3, которые будут являться результатами выполнения операций.
Шаг 2. Так как операции умножения матриц выполняются по законам математики, то точка перед знаком умножения не ставится. Ожидаемый результат умножения двух матриц – матрица из трех строк и трех столбцов.
Шаг 3. Вычисляем обратную матрицу с помощью стандартной функции inv, выводим результат в командную область с помощью оператора disp.
Шаг 4. Вычисляем транспонированную матрицу матрицу с помощью стандартной операции «апостраф» — B’, выводим результат в командную область с помощью оператора disp.
| Программа | Результаты расчетов |
| W1=A*Bdisp(W1)W2=inv(A)disp(W2)W3=B’disp(W3) | — 2. — 3. — 11. — 11. 15. — 50. 8. — 13. 24. — 0.6666667 0.6666667 1. — 0.1333333 0.3333333 0.8 — 0.7333333 0.3333333 0.4 2. 3. 1. — 1. — 5. 2. — 2. 4. 1. |
4) Вычислить определители А и В.
Порядок составления программы таков.
Шаг 1. Выбираем переменные, например, S1, S2, которые будут являться результатами выполнения операций.
Шаг 2. Определители матриц вычисляем в программе с помощью стандартной функции det. Выводим результат в командную область с помощью оператора disp.
| Программа | Результаты расчетов |
| S1=det(A)S2=det(B)disp(S1)disp(S2) | — 15. — 49. |
5) Вычислить вектор V3 поэлементным умножением векторов V1 и V3.
6) Вычислить матрицу D поэлементным умножением матриц A и B.
Порядок составления программы таков.
Шаг 1. Выбираем переменные, например, Z1, Z2, которые будут являться результатами выполнения операций.
Шаг 2. Так как операция умножения двух векторов выполняется поэлементно, то перед знаком умножения ставится точка. Ожидаемый результат поэлементного умножения двух векторов – вектор из трех элементов.
Шаг 3. Так как операция умножения двух матриц выполняется поэлементно, то перед знаком умножения ставится точка. Ожидаемый результат поэлементного умножения двух матриц – матрица из трех строк и трех столбцов.
| Программа | Результаты расчетов |
| Z1=V1.*V3disp(Z1) Z2=A.*Bdisp(Z2) | — 2. — 21. 4. 4. 1. 6. 24. 35. — 24. — 3. 8. 2. |
Индивидуальные варианты приведены в таблице 2.4.
| 1. | A=  B= B=  | 2. | A=  B= B= 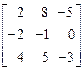 |
| 3. | A=  B= B=  | 4. | A=  B= B=  |
| 5. | A=  B= B=  | 6. | A=  B= B=  |
| 7. | A=  B= B=  | 8. | A=  B= B=  |
| 9. | A=  B= B=  | 10. | A=  B= B=  |
| 11. | A=  B= B=  | 12. | A=  B= B=  |
| 13. | A=  B= B=  | 14. | A=  B= B=  |
| 15. | A=  B= B=  | 16. | A=  B= B=  |
Задание 4. Вычисление суммы и произведения
Постановка задачи. Вычислить сумму и произведение элементов по заданным формулам.
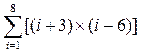 |  |
Порядок составления программы таков.
Шаг 1. Создаем вектор, который будет изменяться от нижнего предела суммирования до верхнего, например, от 1 до 8.
Шаг 2. Создаем вектор F, каждый элемент которого вычисляется по формуле, стоящей под знаком суммирования.
Шаг 3. Находим сумму элементов этого вектора с помощью стандартной функции sum, результат помещаем в переменную SS и выводим ее в командную область с помощью оператора disp.
Шаг 4. Для вычисления произведения проделываем ту же самую последовательность шагов, только воспользуемся стандартной функцией prod.
| Программа | Результаты расчетов | Программа | Результаты расчетов |
| i=1:8F=(i+3).*(i-6)SS=sum(F)disp(SS) | — 48. | i=1:5F1=(i+2*i-1)PP=prod(F1) disp(PP) | 12320. |
Индивидуальные варианты приведены в таблице 2.5.
 |  |
 |  |
 |  |
 |  |
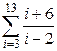 |  |
 | 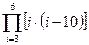 |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Задание 5. Решение задач с матрицами
Постановка задачи.Дана матрица Y(3´4). Вычислить сумму элементов третьей строки и произведение элементов второго столбца матрицы Y. Вычислить максимальный элемент матрицы Y.
Порядок составления программы таков.
Шаг 1. Создаем матрицу, элементы которой подберем самостоятельно. Выведем матрицу в командную область.
Шаг 2. С помощью стандартной функции sum найдем сумму элементов третьей строки, для этого укажем Y(3,:), что означает – третья строка и все столбцы в ней. Поместим сумму в переменную S и выведем результат в командную область.
Шаг 3. Для вычисления произведения проделываем ту же самую последовательность шагов, только воспользуемся стандартной функцией prod и выбираем второй столбец матрицы — Y(:,2). Поместим произведение в переменную S1 и выведем ее в командную область.
Шаг 4. Для вычисления максимума воспользуемся стандартной функцией max, и так как нужно вычислить максимум среди всех элементов матрицы, то номер строки и столбца не указываем. Поместим результат в переменную М и выведем его в командную область.
| Программа | Результаты расчетов |
| Y=[2 -1 -3 8; -7 -6 -3 4; 2 5 8 2]disp(Y)S=sum(Y(3,:))disp(S)S1=prod(Y(:,2))disp(S1)M=max(Y)disp(M) | 2. — 1. — 3. 8. — 7. — 6. — 3. 4. 2. 5. 8. 2. 17. 30. 8. |
Индивидуальные варианты приведены в таблице 2.6.
| № | Дана матрица | Вычислить |
| Y(3´4) | Вычислить сумму элементов третьей строки и произведение элементов второго столбца матрицы Y. Вычислить максимальный элемент матрицы Y. | |
| P(4´3) | Вычислить сумму элементов второй строки и произведение элементов третьего столбца матрицы P. Вычислить максимальный элемент матрицы P. | |
| M(4´4) | Вычислить сумму элементов последней строки и произведение элементов первого столбца матрицы M. Вычислить минимальный элемент матрицы M.. | |
| A(3´3) | Вычислить сумму элементов второй строки и произведение элементов третьего столбца матрицы А. Вычислить минимальный элемент матрицы A. | |
| Y(3´4) | Вычислить сумму элементов второй строки и второго столбца матрицы Вычислить минимальный элемент матрицы Y. | |
| P(4´3) | Вычислить произведение элементов третьей строки и третьего столбца матрицы P. Вычислить максимальный элемент матрицы P. | |
| M(4´4) | Вычислить сумму элементов последней строки и первого столбца матрицы M. Вычислить максимальный элемент матрицы М. | |
| A(3´3) | Вычислить произведение элементов второй строки и третьего столбца матрицы А. Вычислить максимальный элемент матрицы А. | |
| Z(4´3) | Вычислить среднее арифметическое элементов второго столбца матрицы Z. Вычислить минимальный элемент матрицы Z. | |
| P(4´5) | Вычислить среднее арифметическое элементов второй строки матрицы P. Вычислить минимальный элемент матрицы Р. | |
| M(4´4) | Вычислить сумму элементов последней строки и произведение элементов первого столбца матрицы M. Вычислить сумму элементов матрицы М | |
| A(3´3) | Вычислить сумму элементов второй строки и минимальный элемент третьего столбца матрицы А. Вычислить произведение элементов матрицы A. | |
| Y(3´4) | Вычислить максимальный элемент второй строки и произведение элементов второго столбца матрицы Y. Вычислить сумму элементов матрицы Y. | |
| P(4´3) | Вычислить сумму элементов третьей строки и максимальный элемент третьего столбца матрицы P. Вычислить произведение элементов матрицы Р. | |
| M(4´4) | Вычислить сумму элементов последней строки и минимальный элемент первого столбца матрицы M. Вычислить произведение элементов матрицы М. |
Программирование в Scilab
Краткие теоретические сведения
Для программирования разветвляющихся алгоритмов в Scilab существуют оператор условия и оператор выбора.
Условный оператор представлен в нескольких формах и имеет следующий общий вид.
Видео:Бинарный поиск элемента в массивеСкачать

Математические выражения в Scilab
Математические выражения состоят из чисел, констант, переменных, операторов, функций и спецзнаков. Числа могут быть целыми, дробными, с фиксированной и плавающей точкой. Примеры: -3 2.453 123.12е-3. Последнее число – это 123.12*10 -3 , т.е. 0,12312. Для разделения целой и десятичной части числа используется точка. Числа могут быть вещественными и комплексными. Кроме того, в Scilab существуют так называемые системные переменные и символьные константы:
· %i – мнимая единица (%i= 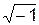
· %pi – число π=3,1415927;
· %e –число е=2,71828184;
· %eps – 2.22d-16;
· %inf – значение машинной бесконечности;
· ans – переменная, хранящая результат последней операции;
· %nan – указание на нечисловой характер данных (not-a-number).
division by zero
division by zero
Системные переменные нельзя переопределить, например, переменной %eps нельзя присвоить другое значение:
—>%eps = 0.1
redefining permanent variable
Символьная константа – это цепочка символов, заключенная в апострофы, например, ‘Hello’.
В Scilab наглядность описания сложных выражений достигается с помощью текстовых комментариев, которые вводят с помощью символов //.
Переменная в Scilab может иметь имя, содержащее сколько угодно символов, но система запоминает и идентифицирует только первые 24 символа. Имя должно начинаться с буквы и может содержать буквы, цифры и символ подчеркивания _.
В памяти компьютера переменные занимают определенное место, называемое рабочим пространством (Workspace). Для очистки рабочего пространства используют функцию clear:
· clear – уничтожение определений всех переменных;
· clear x– уничтожение определения переменной x;
· clear a, b, c– уничтожение определений нескольких переменных.
—> v=[1 2 3 4 5];
—> clear v
undefined variable : v
Большинство операций в Scilab являются матричными операциями, а соответствующие им операторы относятся к матричным операторам. Например, с помощью операторов умножения * и деления / вычисляют произведение и частное от деления двух массивов (векторов или матриц). Есть ряд спецоператоров, например, оператор используют для деления справа налево, а операторы .* и ./ – для поэлементного умножения и деления массивов.
—> v1=[2 4 6 8]; v2=[1, 4, 12, 24]; p=v1/v2, t=v1.*v2, r=v1./v2, h=v1.v2
🔍 Видео
УРОК 5-6. Выполнение арифметических действий над элементами массива (10 класс)Скачать

Как найти количество уникальных элементов в массивеСкачать

Массивы. Описание, ввод и вывод элементов массиваСкачать

С++ для 8 класса, урок 12 (Бинарный поиск корня функции)Скачать

Поток векторного поля через замкнутую поверхностьСкачать

46. Вычисление пределов с помощью эквивалентных бесконечно малых функцийСкачать

Лабораторная работа № 7 по физике для 7 классаСкачать

Теория поиска коротких замыканий с помощью ЛБП и без.Скачать

УРОК 7. Поиск элементов с заданными свойствами. Часть 1. (10 класс)Скачать

Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).Скачать

005 Поиск повторяющихся элементовСкачать

132. Фактор эквивалентности. Число эквивалентности.Скачать

Определение коэффициента вязкости жидкости. Проверка закона СтоксаСкачать

1 Решение задачи графическим и аналитическим методомСкачать