Найти расстояние от точки до образа окружности

Ниже приведена реализация вышеуказанного подхода:

// C ++ программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
#include

using namespace std;

// Функция для поиска кратчайшего расстояния

void dist( double x1, double y1, double x2, double y2, double r)

cout «The shortest distance «

«between a point and a circle is «

sqrt (( pow ((x2 — x1), 2))

double x1 = 4, y1 = 6,

x2 = 35, y2 = 42, r = 5;

dist(x1, y1, x2, y2, r);

// Java-программа для поиска
// Наименьшее расстояние
// между точкой и
// круг

// Функция для поиска кратчайшего расстояния

static void dist( double x1, double y1, double x2,

double y2, double r)

System.out.println( «The shortest distance «

+ «between a point and a circle is «

+ (Math.sqrt((Math.pow((x2 — x1), 2 ))

+ (Math.pow((y2 — y1), 2 )))

public static void main(String[] args)

double x1 = 4 , y1 = 6 ,

x2 = 35 , y2 = 42 , r = 5 ;

dist(x1, y1, x2, y2, r);

/ * Этот код предоставлен PrinciRaj1992 * /

# Python программа для поиска
# Наименьшее расстояние
# между точкой и
# круг

# Функция поиска кратчайшего расстояния

def dist(x1, y1, x2, y2, r):

print ( «The shortest distance between a point and a circle is «

,((((x2 — x1) * * 2 ) + ((y2 — y1) * * 2 )) * * ( 1 / 2 )) — r);

dist(x1, y1, x2, y2, r);

# Этот код предоставлен 29AjayKumar

// C # программа для поиска кратчайшего расстояния
// между точкой и окружностью

// Функция для поиска кратчайшего расстояния

static void dist( double x1, double y1, double x2,

double y2, double r)

Console.WriteLine( «The shortest distance «

+ «between a point and a circle is «

+ (Math.Sqrt((Math.Pow((x2 — x1), 2))

+ (Math.Pow((y2 — y1), 2)))

public static void Main(String[] args)

double x1 = 4, y1 = 6,

x2 = 35, y2 = 42, r = 5;

dist(x1, y1, x2, y2, r);

/ * Этот код предоставлен PrinciRaj1992 * /

// PHP программа для поиска
// Наименьшее расстояние
// между точкой и
// круг

// Функция для поиска кратчайшего расстояния

function dist( $x1 , $y1 , $x2 , $y2 , $r )

echo «The shortest distance between a point and a circle is «

Видео:Расстояние от точки до плоскости. 11 класс.Скачать

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP₁P₂ – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P₁M, P₁P₂) 2 .

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

Видео:Уравнение окружности и формула расстояния между точками на плоскостиСкачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Вычисление расстояний между геометрическими объектами

Видео:Расстояние от точки до плоскости / Вывод формулыСкачать

Линейные многообразия

Видео:Задача 7. Найти расстояние от точки M0 до плоскости, проходящей через три точки M1, M2, M3.Скачать

Расстояние от точки до линейного многообразия (плоскости)

Теорема 1. [1]. Составим квадратную матрицу порядка $ m+1_ $:

Доказательство ☞ ЗДЕСЬ.

Расстояние от точки $ X_ =(x_ ,dots,x_ )^ $ до гиперплоскости (или, в случае $ n=2 $, прямой)

$$ c_1x_1+dots+c_nx_n= h $$ равно $$ d= frac +dots+c_nx_ -h|> > . $$ Ближайшая к $ X_0 $ точка гиперплоскости: $$ X_ =X_0- frac +dots+c_nx_ -h> left(begin c_1 \ vdots \ c_n end right) , . $$

Пусть теперь линейное многообразие (плоскость) задано параметрически $$ mathbb M= subset > $$ при фиксированных столбцах $$ subset ^n . $$ Предположим, что эти столбцы линейно независимы. Составим из них матрицы $$ L=left[ Y_1|dots|Y_k right]_ quad u quad tilde L = left[ Y_1|dots|Y_k| X_0-Y_0 right]_ $$ (здесь $ |_ $ означает конкатенацию).

Теорема 2. Расстояние $ d_ $ от точки $ X_ $ до линейного многообразия $ mathbb M $ вычисляется по формуле

Доказательство. Утверждение теоремы 2 является частным случаем общего результата о вычислении расстояния от точки до линейного многообразия в евклидовом пространстве. ♦

Теорема 3. Ближайшая к точке $ X_0 $ точка многообразия $ mathbb M_ $ (проекция точки на многообразие) определяется по формуле

Доказательство ☞ ЗДЕСЬ.

Пример. Найти расстояние от точки $ X_ =(1,1,1,1)^ $ до плоскости

Ответ. $ d=sqrt approx 0.8808303295 $.

Видео:Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

Расстояние между линейными многообразиями (плоскостями)

Пусть линейные многообразия в $ ^ $ заданы параметрически $$ mathbb M_1= subset mathbb R > ; $$ $$ mathbb M_2= Y_ mid > subset mathbb R > $$ при фиксированных столбцах $$ >subset ^n . $$ Составим из этих столбцов матрицы $$ P=left[ X_1|dots|X_k| Y_1|dots | Y_ right]_ quad u quad tilde P = left[ X_1|dots|X_k| Y_1|dots | Y_ | X_0-Y_0 right]_ $$ (здесь $ |_ $ означает конкатенацию).

Теорема. Расстояние между линейными многообразиями $ mathbb M_1 $ и $ mathbb M_2 $ вычисляется по формуле

Пример. [2]. Найти расстояние между плоскостями

Ответ. $ d=150_ $.

Видео:Лекция 24. Расстояние от точки до прямой на плоскости.Скачать

Квадратичные многообразия (квадрики)

В последующих пунктах, касающихся вычисления расстояний между геометрическими объектами, хотя бы один из которых представлен квадратным уравнением, используется следующая идеология решения. Первоначальной целью ставится построение уравнения расстояний, т.е. алгебраического уравнения от одной переменной, среди корней которого находится квадрат искомого расстояния. После нахождения этого корня, координаты ближайшей точки (или пары ближайших точек) находятся в виде рациональных функций от величины квадрата расстояния. Таким образом, мы «переворачиваем» традиционную схему решения оптимизационных задач:

стационарные точки $ rightarrow $ критические значения

Такая реверсия традиционного подхода оправдана, с одной стороны, тем, что задача сводится к одномерной — поиску корней полинома от одной переменной. Причем нас будет интересовать, как правило, единственный корень этого полинома — минимальный положительный. С другой стороны, уравнение расстояний удается построить в результате чисто алгебраической процедуры: конечного числа элементарных алгебраических операций над коэффициентами уравнений, задающих многообразия. Алгоритм основан на аппарате исключения переменных в системах нелинейных алгебраических уравнений, и ключевым объектом в нем оказывается вычисление дискриминанта полинома (от одной или двух переменных).

Видео:Уравнение окружности (1)Скачать

Расстояние от точки до квадрики

Теорема 1. Пусть квадрика в $ ^ $, задана уравнением

[3]. Квадрат расстояния от начала координат $ in ^ $ до квадрики в $ ^ $, заданной уравнением

$$ X^ AX+2,B^ X-1=0 , $$ равен минимальному положительному корню уравнения расстояний $$ (z)=0, quad npu quad (z)= _ left( f(mu)(mu z-1)-B^ q(A,mu)B right) , $$ и при условии, что указанный корень не является кратным. Здесь $ f(mu_)=det (A-mu E) $ — характеристический полином матрицы $ A_ $, а $ q(A,mu)_ $ — матрица взаимная матрице $ A-mu E_ $.

В частном случае $ B= _ $ (квадрика центрирована к началу координат), имеем:

$$ (z)=left[z^nf(1/z) right]^2 _ (f(mu)) , $$ и расстояние от начала координат до квадрики оказывается равным $ 1/sqrt ^> $, где $ lambda_ ^ $ — максимальное собственное число матрицы $ A_ $.

Пример. Найти расстояние от начала координат до эллипсоида

Ответ. $ d= sqrt approx 1.180968 $.

Нахождение точки на квадрике, ближайшей к заданной точке $ X_ $, возможно с помощью следующего результата.

Теорема 2. При выполнении условий теоремы 1, координаты точки $ X_ $ квадрики, ближайшей к точке $ X_ $ находятся по формуле

$$ X_ =-A^ B — mu_ (A -mu_ E)^ (A^ B+X_0)=(mu_ E- A)^ (B+mu_ X_0) . $$ Здесь $ mu_ $ означает кратный корень полинома $ Phi(mu,z_ ) $, где полином $ Phi(mu,z) $ берется из формулировки теоремы 1, а $ z_ ^ $ означает минимальный положительный корень уравнения расстояний.

Этот результат требует пояснений. Итак, поскольку дискриминант полинома $ Phi(mu,z_ ) $ обращается в нуль, то у этого полинома — как полинома по $ mu_ $ — имеется кратный корень $ mu =mu_ $. Можно доказать [4], что при условии простоты корня $ z=z_ $ уравнения расстояний $ mathcal F(z)=0 $ кратность корня $ mu =mu_ $ для полинома $ Phi(mu,z_ ) $ будет равна ровно $ 2_ $, и других кратных корней этот полином не имеет. Но тогда, выражение для $ mu_ ^ $ может быть найдено в виде рациональной функции коэффициентов полинома $ Phi(mu,z_ ) $. Последнее утверждение может быть доказано разными способами, и в качестве самого наглядного выберем тот, что основан на свойствах дискриминанта, например, на том, что изложено ☞ ЗДЕСЬ.

При выполнении условия предыдущей теоремы, координаты точки $ X_ ^ $, ближайшей на квадрике к точке $ X_ $, являются рациональными функциями от квадрата расстояния.

Точка $ X_ $ квадрики $ X^ AX+2,B^ X-1=0 $, ближайшая к началу координат $ X_0= mathbb O $, находится по формуле:

$$ X_ = — frac )> q(A,mu_ ) B . $$ Здесь $ f(mu_)=det (A-mu E) $ — характеристический полином матрицы $ A_ $, $ q(A,mu)_ $ — матрица взаимная матрице $ A-mu E_ $, а $ mu_ $ означает кратный корень уравнения $$f(mu)(mu z_ -1)-B^ q(A,mu)B=0 , $$ где $ z_ ^ $ — величина квадрата расстояния от $ mathbb O_ $ до квадрики.

Пример. Найти ближайшую к началу координат точку эллипсоида из предыдущего примера.

Проверка. Если подставить вместо $ X_ $ его приближенное значение, то получим: $$ X_ ^ X_ approx mathbf 4, X_ ^ AX_ +2,B^ X_ -1 approx 2.9cdot 10^ , $$ и вектор $ X_ $ перпендикулярен эллипсоиду в точке $ X_=X_ $: $$ AX_ +B approx left(begin 0.040757\ -0.496917 \ 0.456948 end right)approx mu_ X_ . $$

Видео:#30. Как найти расстояние от точки до плоскости?Скачать

Расстояние от линейного многообразия (плоскости) до квадрики

Теорема. [3]. Необходимое и достаточное условие того, что линейное многообразие (плоскость) пересекает эллипсоид зависит от знакоопределенности матрицы $ A_ $:

Условие равенства нулю определителя из теоремы является необходимым и достаточным для существования точки касания эллипсоида и плоскости.

Теорема. [3]. Если условие предыдущей теоремы не выполняется, то квадрат расстояния от эллипсоида до плоскости совпадает с минимальным положительным корнем полинома

Если строки матрицы $ C_ $ ортонормированны, то преобразованием определителя в теореме можно понизить его порядок: выражение под знаком дискриминанта можно преобразовать в

Пример. Найти расстояние от оси $ x_ $ до эллипсоида

$$ 7, x_1^2+6, x_2^2 +5, x_3^2 -4,x_1x_2-4,x_2x_3-37,x_1-12,x_2+3,x_3+54=0 . $$

Расстояния в $ ^ $ от плоскости

$$ c_1x_1+dots+c_nx_n = h iff CX=h $$ до ближайшей и до самой дальней точек эллипсоида $$ X^ AX+2B^ X-1=0 , (A=A^ ) $$ совпадают с модулями корней полинома: $$ (Z)=left| begin A & B & C^ /|C|\ B^ & -1 & Z-h/|C|\ C/|C| & Z-h/|C| & 0 end right| . $$ Здесь $ |C|=sqrt > $ и предполагается, что поверхности не пересекаются.

Пример. Найти расстояние от прямой $ 2, x_1- x_ =0 $ до эллипса

$$ 7,x_1^2-4,x_1x_2 + 6, x_2^2-47, x_1 -24, x_ +124 = 0 .$$

Ответ. $$ d = left| -frac sqrt + frac sqrt right| approx 0.809219_ . $$

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Расстояние между квадриками

Теорема. Пусть $ X^ A_ X =1 $ и $ X^ A_ X =1 $ – квадрики в $ ^ $, причем первая является эллипсоидом. Квадрики не пересекаются тогда и только тогда, когда матрица $ A_ -A_2 $ является знакоопределенной.

Доказательство ☞ ЗДЕСЬ.

Теорема. [3,4]. Если выполняется условие предыдущей теоремы, то квадрат расстояния между

$$ mbox X^ A_ X =1 mbox X^ A_ X =1 $$ совпадает с минимальным положительным корнем уравнения расстояний $$ (z)=0 quad npu quad (z)= _ left( Phi(lambda,z) right) . $$ Здесь $$ Phi(lambda,z)=det (lambda A_1 + (z- lambda) A_2 — lambda (z-lambda) A_1 A_2), $$ $ _ $ — дискриминант полинома рассматриваемого относительно переменной $ lambda_ $. Дополнительно предполагается, что указанный корень не является кратным.

Пример. Найти расстояние между эллипсами

$$10,x_1^2-12,x_1x_2+8,x_2^2=1 qquad u qquad x_1^2+x_1x_2+x_2^2=1 . $$

Ответ. $ d_= sqrt approx 0.23226206 $.

Нахождение координат ближайших точек на квадриках (обеспечивающих найденное расстояние) возможно по алгоритму:

1. Если $ z=z_ $ — корень полинома $ (z) $, то это значит, что полином $$ Phi(lambda, z_ ) = det ( lambda A_1 +(z_ -lambda)A_2 — lambda (z_ -lambda) A_2A_1) $$ имеет кратный корень $ lambda_ = lambda_ $. При выполнении условий теоремы, этот корень будет единственным второй кратности и его можно выразить в виде рациональной функции от $ z_ $ с помощью субдискриминантов.

2. Столбец координат $ X_ ^ $ точки первой квадрики, удовлетворяет тогда однородной системе уравнений $$ ( lambda_ A_1 +(z_ -lambda_ )A_2 — lambda_ (z_ -lambda_ ) A_2A_1) X = mathbb O , $$ которая имеет бесконечное множество решений, поскольку определитель ее матрицы равен нулю. Из этого бесконечного множества мы выделяем те решения, что удовлетворяют условию $ X^ A_ X=1 $.

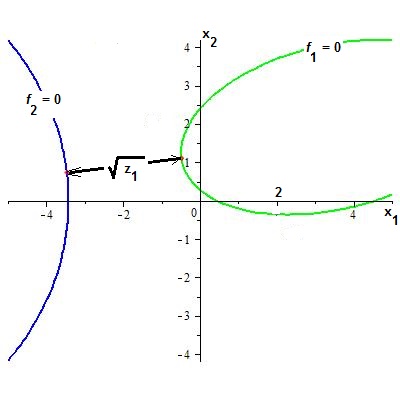
При выполнении условий теоремы таких решений будет два (что соответствует симметрии задачи, см. рисунок).

Аналогично, столбец координат $ Y_ ^ $ точки на второй квадрике $ Y^ A_ Y=1_ $ будет решением системы уравнений $$ ( lambda_ A_1 +(z_ -lambda_ )A_2 — lambda_ (z_ -lambda_ ) A_1A_2) Y = mathbb O . $$

Для нахождения решений воспользуемся одним из результатов теории систем линейных уравнений. Составим столбец из алгебраических дополнений к элементам какой-либо строки матрицы $$ M= lambda_ A_1 +(z_ -lambda_ )A_2 — lambda_ (z_ -lambda_ ) A_2A_1 . $$ Тогда вектор $ X_ ^ $ отличается от этого столбца лишь множителем, который определится из условия $ X^ A_ X=1_ $. Аналогично, для получения столбца координат $ Y_ ^ $ возьмем столбец из алгебраических дополнений к элементам какого-либо столбца той же матрицы $ M_ $ и домножим его на константу, чтобы обеспечить выполнение условия $ Y^ A_ Y=1_ $.

3. Получившиеся пары $ X_ ,Y_ ^ $ надо согласовать: они должны подчиняться условию $$ (X_ -Y_ )^ (X_ -Y_ )=z_ . $$

Пример. Найти ближайшие точки эллипсов из предыдущего примера.

Ответ. $ pm (0.3838312,, 0.4418639)_ $ и $ pm (0.5449964,, 0.6091105)_ $ соответственно (знаки должны быть согласованы).

Теорема. [3,4].Пусть

$$ X^ A_ X+2,B^ _1X-1=0 mbox X^ A_ X+2,B^ _2X-1=0 $$ — квадрики в $ ^ _ $, причем первая является эллипсоидом. Квадрики пересекаются тогда и только тогда, когда среди вещественных корней полинома

Для того, чтобы существовала точка касания квадрик

$$ X^ A_ X+2,B^ _1X-1=0 mbox X^ A_ X+2,B^ _2X-1=0 $$ необходимо и достаточно, чтобы было выполнено условие $$ _lambda left( det left( left[ begin A_2 & B_2\ B_2^ & -1 end right] — lambda left[ begin A_1 & B_1\ B_1^ & -1 end right] right) right) =0 . $$

Теорема. [3,4]. Если не выполняется условие предыдущей теоремы, то квадрат расстояния между

Пример. Найти расстояние между эллипсами

Ответ. $ d approx sqrt approx 3.00306481 $.

Нахождение ближайших точек на квадриках (обеспечивающих найденное расстояние) возможно по следующему алгоритму.

2. Составим матрицу $$ M= mu_ A_1+mu_ A_2-A_2A_1 . $$ Тогда координатные столбцы ближайших точек на квадриках вычисляются по формулам: $$ X_ =M^ (A_2B_1-mu_ B_1-mu_ B_2), Y_ =(M^ )^ > (A_1B_2 — mu_ B_1-mu_ B_2). $$

Пример. Найти ближайшие точки эллипсов из предыдущего примера.

Проверка. $$ (X_ -Y_ )^ (X_ -Y_ )approx mathbf 3 , $$ $$ X_ ^ A_1X_ +2B_1^ X_ -1 approx 1cdot 10^ , Y_ ^ A_2Y_ +2B_2^ Y_ -1approx -3cdot 10^ , $$ и вектор $ X_ -Y_ ^ $ перпендикулярен обоим эллипсам в соответствующих ближайших точках: $$ A_1X_ +B_1= left(begin 1.767863990 \ 0.219610712 end right)=mu_ (X_ -Y_ ), A_2Y_ +B_2= left(begin -0.1254448880 \ -0.0155832356 end right)=-mu_ (X_ -Y_ ) . $$

Пример. Найти расстояние между эллипсоидами

$$ 7,x_1^2+6,x_2^2+5,x_3^2-4,x_1x_2-4,x_2x_3-37,x_1-12,x_2+3,x_3+54=0$$ и $$ 189,x_1^2+x_2^2+189,x_3^2+2,x_1x_3-x_2x_3-27=0 .$$

Ответ. $ d approx sqrt approx 1.1635198754_ $

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Алгебраические кривые и многообразия

Видео:расстояние от точки до плоскостиСкачать

Расстояние от точки до плоской алгебраической кривой

Задача. Пусть алгебраическая кривая задана уравнением $$ Phi(x,y)=0 . $$ Здесь $ Phi_(x,y) $ — отличный от константы полином от $ x_ $ и $ y_ $ с вещественными коэффициентами. Требуется найти расстояние до этой кривой от начала координат.

Здесь возникает проблема, которую для рассмотренных выше случаев удавалось либо обойти, либо же сравнительно дешево решить: это проблема существования решения. Дело в том, что уравнение может не иметь вещественных решений, то есть не определять никакой кривой на плоскости $ mathbb R^ $.

Будем решать задачу сначала для частного случая — пусть полином $ Phi_(x,y) $ является четным по переменной $ y_ $. Геометрически это означает, что кривая (если она существует) будет зеркально симметричной относительно оси $ mathbb Ox $. А с аналитической точки зрения такой полином можно представить в виде полинома $$ F(x,Y) equiv Phi_(x,y) quad npu quad Y=y^2 . $$

Теорема 1 [6]. Пусть $ Phi_(x,y) equiv Phi_(x,-y) $. Уравнение $ Phi_(x,y)=0 $ не имеет вещественных решений если одновременно выполняются два условия:

a) уравнение $ Phi(x,0)=0 $ не имеет вещественных решений;

б) уравнение $$ mathcal F(z)=mathcal D_x( F(x,z-x^2))=0 $$ не имеет положительных решений.

Если хотя бы одно из этих условий не выполняется, то квадрат расстояния от начала координат до кривой $ Phi(x_,y)=0 $ равен либо квадрату минимального по модулю вещественного корня уравнения $ Phi(x,0)=0 $, либо же минимальному положительному корню уравнения $ mathcal F(z)= 0 $, при условии, что последний не является кратным. Здесь $ _ $ — дискриминант полинома, рассматриваемого относительно переменной $ x_ $.

Пример. Найти расстояние от начала координат до кривой

Решение. Уравнение $$ Phi(x,0)=x^6-6,x^5+25,x-45=0 $$ имеет вещественные корни $ mu_1approx -1.621919 $ и $ mu_2 approx 5.986387 $. 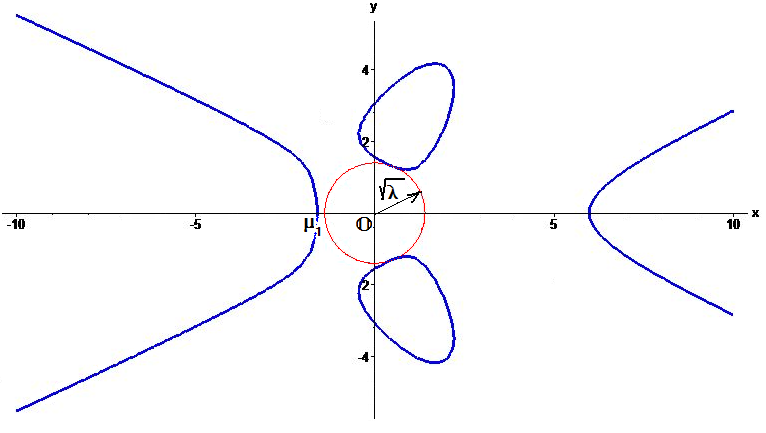Далее, $$ F(x,Y)=x^6-5,x^4Y-Y^3-6,x^5+6,xY^2+10,Y^2+25,x-45 $$ и полином $$ mathcal F(z)=mathcal D_x (F(x,z-x^2))= ,z^ — z^ — ,z^ + ,z^ + z^ $$ $$ — z^ + ,z^9+ ,z^8- ,z^7+ ,z^6+ $$ $$ + z^5 — ,z^4+ ,z^3+ ,z^2- , z+ $$ $$ + $$ имеет минимальный положительный корень равный $ lambda approx 1.965293 $. Поскольку $ sqrt 4) , задача о трёх заводах.

Пример. В точках $ P_ ,P_2,P_3 $ расположены источники полезных ископаемых: железной руды, угля и воды соответственно. Известно, что для производства одной тонны стали необходимо иметь $ m_ $ тонн руды, $ m_2 $ тонн угля и $ m_3 $ тонн воды. В предположении, что стоимость перевозки одной тонны груза не зависит от его природы, где следует расположить сталелитейное производство так, чтобы минимизировать транспортные издержки?

Подробное обсуждение этой задачи (и к ней примыкающих) ☞ ЗДЕСЬ.

Задача о точке Лемуана-Греба

Задача. Найти точку плоскости, cумма квадратов расстояний от которой до сторон треугольника, лежащего в этой же плоскости, минимальна.

Решение. Пусть $ d_1, d_2,d_3 $ — расстояния от точки $ P_ $ плоскости до сторон треугольника с длинами $ D_1, D_2, D_3 $ соответственно. Воспользуемся тождеством Лагранжа: $$ (d_1^2+ d_2^2+d_3^2)(D_1^2+ D_2^2+D_3^2)equiv $$ $$ equiv (d_1D_1+ d_2D_2+d_3D_3)^2+(d_1D_2-d_2D_1)^2+(d_2D_3-d_3D_2)^2+ (d_1D_3-d_3D_1)^2 . $$ Величина $ d_1D_1+ d_2D_2+d_3D_3 $ является постоянной, не зависящей от координат точки $ P_ $: $$ d_1D_1+ d_2D_2+d_3D_3 =2S , $$ где $ S_ $ — площадь данного треугольника. Следовательно $ min (d_1^2+d_2^2+d_3^2) $ достигается при условиях $$ d_1D_2-d_2D_1=0, d_2D_3-d_3D_2=0, d_1D_3-d_3D_1=0 , $$ то есть когда $$ frac =frac =frac . $$ Определяемая этими соотношениями точка называется точкой Лемуана 6) или точкой Греба 7) ; в ней пересекаются симедианы треугольника.

Еще некоторые задачи

Построение прямой на плоскости, сумма квадратов расстояний до которой от заданных точек минимальна ☞ ЗДЕСЬ

Видео:Расстояние от точки до плоскостиСкачать

Наименьшее расстояние между точкой и окружностью

Данный круг с данным радиусом имеет свой центр в определенной позиции в координатной плоскости. В координатной плоскости задается другая точка. Задача — найти кратчайшее расстояние между точкой и окружностью.

Примеры:

Подход :

Ниже приведена реализация вышеуказанного подхода:

// C ++ программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
#include

using namespace std;

// Функция для поиска кратчайшего расстояния

void dist( double x1, double y1, double x2, double y2, double r)

cout «The shortest distance «

«between a point and a circle is «

sqrt (( pow ((x2 — x1), 2))

double x1 = 4, y1 = 6,

x2 = 35, y2 = 42, r = 5;

dist(x1, y1, x2, y2, r);

// Java-программа для поиска
// Наименьшее расстояние
// между точкой и
// круг

// Функция для поиска кратчайшего расстояния

static void dist( double x1, double y1, double x2,

double y2, double r)

System.out.println( «The shortest distance «

+ «between a point and a circle is «

+ (Math.sqrt((Math.pow((x2 — x1), 2 ))

+ (Math.pow((y2 — y1), 2 )))

public static void main(String[] args)

double x1 = 4 , y1 = 6 ,

x2 = 35 , y2 = 42 , r = 5 ;

dist(x1, y1, x2, y2, r);

/ * Этот код предоставлен PrinciRaj1992 * /

# Python программа для поиска
# Наименьшее расстояние
# между точкой и
# круг

# Функция поиска кратчайшего расстояния

def dist(x1, y1, x2, y2, r):

print ( «The shortest distance between a point and a circle is «

,((((x2 — x1) * * 2 ) + ((y2 — y1) * * 2 )) * * ( 1 / 2 )) — r);

dist(x1, y1, x2, y2, r);

# Этот код предоставлен 29AjayKumar

// C # программа для поиска кратчайшего расстояния
// между точкой и окружностью

// Функция для поиска кратчайшего расстояния

static void dist( double x1, double y1, double x2,

double y2, double r)

Console.WriteLine( «The shortest distance «

+ «between a point and a circle is «

+ (Math.Sqrt((Math.Pow((x2 — x1), 2))

+ (Math.Pow((y2 — y1), 2)))

public static void Main(String[] args)

double x1 = 4, y1 = 6,

x2 = 35, y2 = 42, r = 5;

dist(x1, y1, x2, y2, r);

/ * Этот код предоставлен PrinciRaj1992 * /

// PHP программа для поиска
// Наименьшее расстояние
// между точкой и
// круг

// Функция для поиска кратчайшего расстояния

function dist( $x1 , $y1 , $x2 , $y2 , $r )

echo «The shortest distance between a point and a circle is «

📺 Видео

Окружность и круг, 6 классСкачать

Расстояние от точки до прямойСкачать

Расстояние от точки до плоскостиСкачать

Определить расстояние от точки С до прямой АВ. Метод прямоугольного треугольника.Скачать

Найти центр и радиус окружностиСкачать