Найти площадь и высоту треугольника по векторам

Этот онлайн калькулятор позволит вам очень просто найти площадь треугольника построенного на векторах.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади треугольника построенного на векторах и закрепить пройденый материал.

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Калькулятор для вычисления площади треугольника построенного на векторах

Выберите каким образом задается треугольник:

Введите значения векторов: Введите координаты точек:

Инструкция использования калькулятора для вычисления площади треугольника построенного на векторах

Ввод данных в калькулятор для вычисления площади треугольника построенного на векторах

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора вычисления площади треугольника построенного на векторах

• Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Видео:Площадь треугольника, построенного на векторахСкачать

Теория. Площадь треугольника построенного на векторах

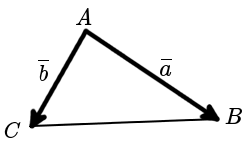
Определение Площадь треугольника образованного векторами a и b равна половине модуля векторного произведения этих векторов:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Вычисляем высоту через координаты вершин 1Скачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Калькулятор онлайн.
Вычисление площади треугольника построенного на векторах.

Этот калькулятор онлайн вычисляет площадь треугольника построенного на векторах. Треугольник может быть задан координатами двух векторов или координатами трех вершин треугольника.

Онлайн калькулятор для вычисления площади треугольника построенного на векторах не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac )

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac )

Видео:Площадь параллелограмма, построенного на данных векторахСкачать

Площадь треугольника по координатам вершин — формулы для расчета

Видео:Найдите площадь параллелограмма, построенного на векторахСкачать

Самый простой многоугольник и вектор

Чтобы найти площадь треугольника через векторы и известные координаты его вершин, необходимо подробнее познакомиться с этими геометрическими объектами. Знание их свойств позволяет легко вычислять разные характеристики изучаемой фигуры, включая периметр, высоту, углы при вершинах и другие. При этом используются универсальные математические операции, которые можно применять с успехом не только для треугольника, но и для других многоугольников.

Фигура на плоскости

Треугольник в геометрии представляет собой самый простой многоугольник, который лежит всегда в одной плоскости, даже если фигура рассматривается в трехмерном пространстве. Состоит он из сторон и вершины.

Сторон и вершин у фигуры по три. Сторона является отрезком, а вершина — это точка пересечения этих отрезков. Для нее характерен определенный угол. Все углы треугольника являются разными в общем случае, их сумма всегда соответствует 180°. Однако, существуют специальные типы фигуры, для которых либо два угла равны друг другу (равнобедренный), либо все три (равносторонний). В задачах называют треугольники по имени их трех вершин, обозначенных латинскими буквами, например, ABC или NPQ.

Для треугольника важное значение имеют следующие отрезки:

• делящий противоположную углу сторону пополам — медиана;
• разделяющий угол при вершине на два равных — биссектриса;
• падающий под прямым углом на противоположную углу сторону — высота.

Высота, например, используется для расчета площади фигуры. Для равностороннего треугольника все эти отрезки совпадают друг с другом для любой вершины, а для равнобедренного они одинаковы лишь для угла, образованного равными сторонами.

Направленный отрезок

Вектором называют линейный элемент, который имеет начало и конец. Для его определения удобнее всего использовать координатную плоскость. Она представляет собой две направленные оси, имеющие шкалу и пересекающиеся под углом 90°. Точка пересечения является началом координат и обозначается буквой O (0; 0). Здесь каждая из цифр указывает точку пересечение перпендикуляра, опущенного из рассматриваемого объекта к каждой из двух осей.

Если начало A (x0; y0) и конец B (x1; y1) вектора известны, тогда легко можно вычислить его собственные координаты. Делается это так:

AB- = B-A = (x1-x0; y1-y0).

Иными словами, чтобы получить вектор AB-, следует из соответствующих координат его конца вычесть его начало. Эта операция эквивалентна параллельному перемещению AB- в начало координатной плоскости, что говорит о существовании бесконечного количества одинаковых AB-векторов.

Направленные отрезки можно складывать, вычитать и умножать. Для каждой из операций существуют определенные правила. Если для сложения и вычитания речь идет о геометрических особенностях, то в случае умножения применяются исключительно алгебраические выражения. Вектор a- можно умножить на b- двумя принципиально разными способами:

1. Скалярно: (a-*b-). В этом случае мы получаем число. Правило умножения записывается следующим образом: (a-*b-) = |a-|*|b-|*cos (ab)=x1*x2+y1*y2. Здесь знаком модуля (||) обозначены длины соответствующих отрезков, cos (ab) — это косинус угла между a- и b-, при этом a-(x1; y1), b-(x2; y2). Этот тип произведения можно использовать для вычисления углов между направленными отрезками, а также для определения объема фигур в пространстве.
2. Векторно: [a-*b-]. Результатом этой операции является вектор, который перпендикулярен исходным, его направление (вверх или вниз) принято определять по правилу правой руки: четыре пальца должны быть направлены от конца a- к концу b-, тогда оттопыренный большой палец укажет направление их векторного произведения. Длина этого перпендикулярного вектора определяется так: [a-*b-] = |a-|*|b-|*sin (ab) = x1*y2-x2*y1. Векторное произведение используют для вычисления площадей фигур.

Видео:Площадь параллелограмма по векторамСкачать

Методы вычисления площади по координатам

Задачи на вычисление площадей, периметров или объемов фигур по известным координатам их вершин являются типичными для школьного курса геометрии. В связи с развитием современных технологий школьники часто ищут в интернете, как решить треугольник онлайн по координатам. Тем не менее, существует ряд простых способов, которые позволяют быстро найти площадь фигуры, если известно расположение трех его вершин на координатной плоскости.

Универсальный подход

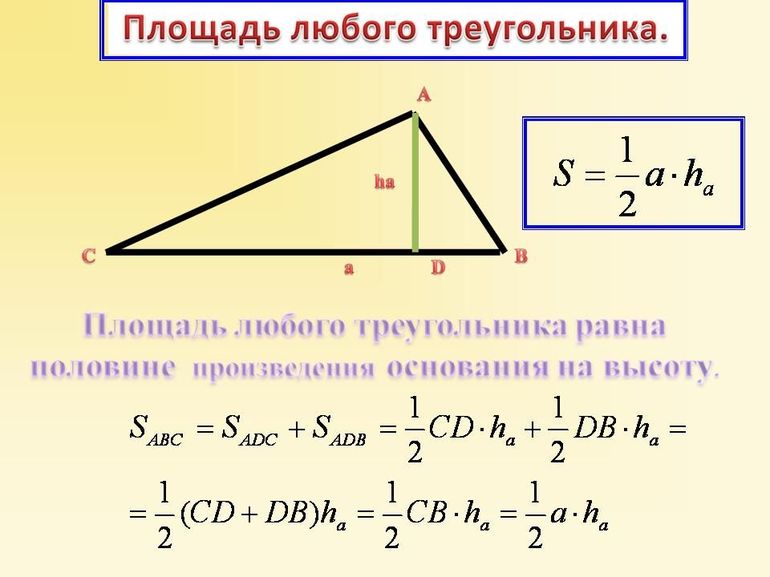
Этот метод можно применять всегда, независимо от того, какой тип треугольника рассматривается. Известно, что площадь фигуры вычисляется, как произведение половины стороны на опущенную на нее высоту: S = ½*a*h.

Пусть имеются координаты вершин заданного треугольника ABC:

Тогда координаты его векторов AB- и AC- выразятся так:

Если провести высоту h треугольника ABC к любой из этих сторон, например, к AC, то ее длина может быть рассчитана с использованием тригонометрической функции синуса:

Здесь α является углом между векторами-сторонами AB- и AC-. Тогда формулу площади можно переписать в следующем виде: S = ½*a*h = ½*AC* AB*sin (α).

Можно заметить, что записанное выражение является не чем иным, как векторным произведением для AB- и AC-, поэтому можно переписать формулу для S так:

S = ½*[ AB-* AC- ] = ½*((x2-x1)*(y3-y1) — (y2-y1)*(x3-x1)).

Можно аналогично показать, что подобные выражения получаются для пар векторов AC-, BC- и AB-, BC-.

Рекомендуется не запоминать конечные выражения для площади треугольника, поскольку они являются несколько громоздкими, и при их использовании ученики могут запутаться. Для решения подобного рода задач достаточно понять свойства векторов и единственную универсальную формулу для S для любого типа треугольников.

Любопытно отметить, что векторное произведение при вычислении площади можно применять не только для треугольников, но и для любых четырехугольников. Так, в случае параллелограмма рассматриваемая характеристика будет точно равна векторному произведению любых смежных (непараллельных) его сторон.

Использование формулы Герона

Этот способ также может считаться универсальным, поскольку он применим к любым типам треугольников. В работе Герона Александрийского, которая называется «Метрика» и относится к I веку нашей эры, впервые было обнаружено выражение, позволяющее по длинам сторон рассматриваемой фигуры определить ее площадь. Формула имеет следующий вид:

Здесь p — полупериметр, a, b, c — длины сторон.

Последовательность этапов решения задачи можно выразить таким образом:

1. Необходимо определить координаты векторов, образующих стороны треугольника.
2. Затем, следует вычислить длины их сторон.
3. Посчитать полупериметр фигуры.
4. Применить формулу Герона.

Ключевым этапом является определение длины вектора. Пусть AB- имеет координаты (x1; y1), тогда его длина вычисляется так:

|AB-| = (x1 2 + y1 2 )^0,5.

Длина любого вектора как на плоскости, так и в пространстве, вычисляется, как сумма квадратов всех его координат, взятых под корень.

Очевидно, что можно записать общее выражение для площади треугольника через координаты с использованием формулы Герона, но оно будет слишком громоздким, поэтому нет никакого смысла запоминать его.

Другие способы

Существуют эмпирические правила, которые можно запомнить и легко решать задачи на определение площади треугольника. Пусть координаты его вершин задаются так: A (x1; y1), B (x2; y2), C (x3; y3). Предположим, что порядок вершин A, B, C расположен против часовой стрелки, тогда существуют следующие правила определения площади ABC:

1. Можно воспользоваться формулой: S = ½*(x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)). То есть выбирается первая координата вершины и умножается на разность вторых координат двух других вершин, возникающих против хода стрелки часов от первой. Затем, все три члена складываются и делятся на 2.
2. Матричный способ. Необходимо выписать в столбик пары координат каждой вершины против часовой стрелки и завершить координатами исходной. После этого следует сложить три попарных произведения первой и второй координат двух соседних вершин, а затем, вычесть три попарных произведений второй и первой координат тех же вершин. Результат поделить пополам. Например: (x1; y1) (x2; y2) (x3; y3) (x1; y1). S = ½*(x1*y2 + x2*y3 + x3*y1 — y1*x2 — y2*x3 — y3*x1).

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Решение задачи

Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).

Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:

Чтобы рассчитать площадь, достаточно вычислить полупроизведение векторное для выбранных направленных отрезков: S = ½*[AB-*BC-] = ½*(1*(-7)-8*(-4)) = 12,5 квадратных единиц.

Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.

📹 Видео

Высшая математика. 3 урок. Аналитическая геометрия. Вычисление площади треугольникаСкачать

Задача о векторах, построенных на медиане, биссектрисе и высоте треугольникаСкачать

Вычисление медианы, высоты и угла по координатам вершинСкачать

Найти площадь треугольника на векторахСкачать

§20 Нахождение объёма параллелипипедаСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Уравнения стороны треугольника и медианыСкачать

Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать