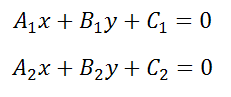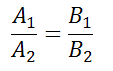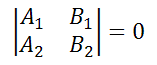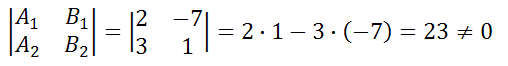Необходимым и достаточным условием параллельности двух прямых, заданных уравнением:
служит равенство их угловых коэффициентов, то есть
Если прямые заданы уравнениями в общем виде, то есть
то условие параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны:
или в другом представлении 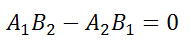
Также это равенство можно записать в виде
Если свободные члены пропорциональны, то есть,
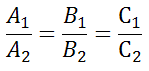
то прямые не только параллельны, но и совпадают.
4x+2y-8=0 и 8x+4y-16=0
представляют одну и ту же прямую, то есть совпадают.
Пример 2
Прямые у=4x-3 ( на графике синего цвета ) и y=4x+7 ( прямая красного цвета ) параллельны, так как у них угловые коэффициенты равны k1=k2=4
Пример 3
Прямые у=5x+1 и y=3x-4 не параллельны, так как у них угловые коэффициенты не равны, т.е. k1=5, k2=3
Пример 4
Прямые 2x+4y+7=0 и 3x+6y-5=0 параллельны, так как выражение равно нулю
Пример 5
Прямые 2x-7y+7=0 и 3x+y-5=0 не параллельны, так как выражение не равно нулю
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Аналитическая геометрия для «чайников»
Настоящая книга позволит вам в сжатые сроки (2-3 недели) освоить основы аналитической геометрии и научиться решать наиболее распространённые задачи по теме. Материал предназначен для студентов-заочников и других читателей, которые хотят быстро освоить минимум теории и максимум практики
Сначала немного о предмете…. Наверняка вам сейчас вспомнился курс школьной геометрии с многочисленными теоремами, их доказательствами, чертежами и т.д. Что скрывать, нелюбимый и часто малопонятный предмет для значительной доли учеников. Аналитическая геометрия, как ни странно, может показаться более интересной и доступной. Что означает «аналитическая»? На ум сразу приходят два «штампованных» математических оборота: графический метод решения и аналитический метод решения.
Графический метод связан с построением графиков, чертежей. Аналитический же метод предполагает решение задач преимущественно посредством алгебраических действий. В этой связи алгоритм решения многих задач аналитической геометрии прост и прозрачен, зачастую достаточно аккуратно применить нужные формулы – и ответ готов! Нет, конечно, совсем без чертежей тут не обойдется, к тому же для лучшего понимания материала я постараюсь приводить их сверх необходимости.
Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Расстояние между прямыми в пространстве онлайн
С помощю этого онлайн калькулятора можно найти расстояние между прямыми в пространстве. Дается подробное решение с пояснениями. Для вычисления расстояния между прямыми в пространстве, задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Расстояние между прямыми в пространстве − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
 . . | (1) |
 , , | (2) |
Прямые (1) и (2) в пространстве могут совпадать, быть паралленьными, пересекаться, или быть скрещивающимся. Если прямые в пространстве пересекаются или совпадают, то расстояние между ними равно нулю. Мы рассмотрим два случая. Первый − прямые параллельны, и второй − прямые скрещиваются. Остальные являются частыми случаями. Если при вычислении расстояния между параллельными прямыми мы получим расстояние равным нулю, то это значит, что эти прямые совпадают. Если же расстояние между скрещивающимися прямыми равно нулю, то эти прямые пересекаются.
1. Расстояние между параллельными прямыми в пространстве
Рассмотрим два метода вычисления расстояния между прямыми.
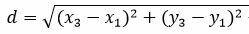  |
которое и является расстоянием между прямыми L1 и L2 (Рис.1).
 |
Пример 1. Найти расстояние между прямыми L1 и L2:
 | (3) |
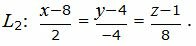 | (4) |
| q1=<m1, p1, l1>= |
| q2=<m2, p2, l2>= |
Найдем проекцию точки M1 на прямую L2. Для этого построим плоскость α, проходящей через точку M1 и перпендикулярной прямойL2.
Для того, чтобы плоскость α было перепендикулярна прямой L2, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L2, т.е. в качестве нормального вектора плоскости α можно взять направляющий вектор прямой L2. Тогда уравнение искомой плоскости, проходящей через точку M1(x1, y1, z1) имеет следующий вид:
| m2<x−x1)+p2(y−y1)+ l2(z−z1)=0 | (5) |
| 2(x−1)−4(y−2)+ 8(z−1)=0 |
После упрощения получим уравнение плоскости, проходящей через точку M1 и перпендикулярной прямой L2:
| 2x−4y+ 8z−2=0 | (6) |
Найдем точку пересечения прямой L2 и плоскости α, для этого построим параметрическое уравнение прямой L2.
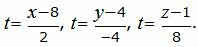 |
Выразив переменные x, y, z через параметр t, получим параметрическое уравнение прямой L2:
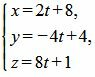 | (7) |
Чтобы найти точку пересечения прямой L2 и плоскости α, подставим значения переменных x, y, z из (7) в (6):
 |
Решив уравнение получим:
 | (8) |
Подставляя полученное значение t в (7), получим точку пересеченияпрямой L2 и плоскости α:
 |
Остается найти расстояние между точками M1 и M3:
 |
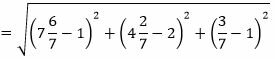  |
Ответ: Расстояние между прямыми L1 и L2 равно d=7.2506.
Метод 2. Найдем расстояние между прямыми L1 и L2 (уравнения (1) и (2)). Во первых, проверяем параллельность прямых L1 и L2. Если направляющие векторы прямых L1 и L2 коллинеарны, т.е. если существует такое число λ, что выполнено равенство q1=λq2, то прямые L1 и L2 параллельны.
Данный метод вычисления расстояния между параллельными векторами основана на понятии векторного произведения векторов. Известно, что норма векторного произведения векторов 
 |
Вычислим координаты вектора 
 |
Вычислим векторное произведение векторов 
 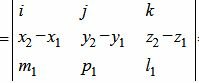 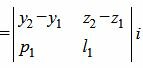  |
Вычисляя определители второго порядка находим координаты вектора c:
Далее находим площадь параллелограмма:
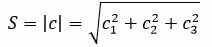 . . |
Расстояние между прямыми L1 и L2 равно:
 , , |
 , , |
Пример 2. Решим пример 1 методом 2. Найти расстояние между прямыми
 | (25) |
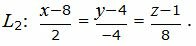 | (26) |
| q1=<m1, p1, l1>= |
| q2=<m2, p2, l2>= |
Векторы q1 и q2 коллинеарны. Следовательно прямые L1 и L2 параллельны. Для вычисления расстояния между параллельными прямыми воспользуемся векторным произведением векторов.
Построим вектор 
Вычислим векторное произведение векторов 

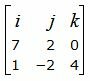 |
Вычислим определитель этой матрицы, разложив ее по первой строке. Результатом этих вычислений получим векторное произведение векторов 
   |
Таким образом, результатом векторного произведения векторов 
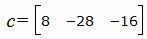 |
Поскольку векторное произведение векторов 
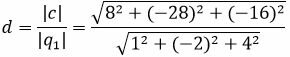  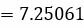 |
Ответ: Расстояние между прямыми L1 и L2 равно d=7.25061.
2. Расстояние между скрещивающимися прямыми в пространстве
Пусть задана декартова прямоугольная симтема координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 (уравнения (1) и (2)).
Пусть прямые L1 и L2 не параллельны (паралельные прямые мы расстотрели в предыдущем параграфе). Чтобы найти расстояние между прямыми L1 и L2 нужно построить параллельные плоскости α1 и α2 так, чтобы прямая L1 лежал на плоскости α1 а прямая L2 − на плоскости α2. Тогда расстояние между прямыми L1 и L2 равно расстоянию между плоскостями L1 и L2 (Рис. 3).
 |
Поскольку плоскость α1, проходит через прямую L1, то он проходит также через M1(x1, y1, z1). Следовательно справедливо следующее равенство:
| A1x1+B1y1+C1z1+D1=0. | (27) |
где n1=<A1, B1, C1> − нормальный вектор плоскости α1. Для того, чтобы плоскость α1 проходила через прямую L1, нормальный вектор n1 должен быть ортогональным направляющему вектору q1 прямой L1, т.е. скалярное произведение этих векторов должен быть равным нулю:
| A1m1+B1p1+C1l1=0. | (28) |
Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:
| A1m2+B1p2+C1l2=0. | (29) |
Решая систему линейных уравнений (27)−(29), с тремя уравнениями и четыремя неизвестными A1, B1, C1, D1, и подставляя в уравнение
| A1x+B1y+C1z+D1=0. | (30) |
получим уравнение плоскости α1. (Как построить уравнение плоскости, проходящей через прямую, параллельно другой прямой подробно изложено здесь).
Аналогичным образом находим уравнение плоскости α2:
| A2x+B2y+C2z+D2=0. | (31) |
Плоскости α1 и α2 параллельны, следовательно полученные нормальные векторыn1=<A1, B1, C1> и n2=<A2, B2, C2> этих плоскостей коллинеарны. Если эти векторы не равны, то можно умножить (31) на некторое число так, чтобы полученный нормальный вектор n2 совпадал с нормальным вектором уравнения (30).
Тогда расстояние между параллельными плоскостями вычисляется формулой:
 . . |
Полученное расстояние между плоскостями α1 и α2 является также расстоянием между прямыми L1 и L2.
Пример 3. Найти расстояние между прямыми
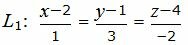 | (32) |
 | (33) |
Построим плоскость α1, проходящую через прямую L1, параллельно прямой L2.
Поскольку плоскость α1 проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(2, 1, 4) и нормальный вектор n1=<m1, p1, l1> плоскости α1 перпендикулярна направляющему вектору q1 прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
| A1x1+B1y1+C1z1+D1=0. | (34) |
а условие параллельности прямой L1 и искомой плоскости α1 представляется следующим условием:
| A1m1+B1p1+C1l1=0. | (35) |
Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:
| A1m2+B1p2+C1l2=0. | (36) |
| A1·2+B1·1+C1·4+D1=0. | (37) |
| A1·1+B1·3+C1·(−2)=0. | (38) |
| A1·2+B1·(−3)+C1·7=0. | (39) |
Представим эти уравнения в матричном виде:
 | (40) |
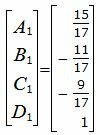 | (41) |
Искомая плоскость может быть представлена формулой:
| A1x+B1y+C1z+D1=0. | (42) |
 |
Упростим уравнение, умножив на число 17.
 | (43) |
Построим плоскость α2, проходящую через прямую L2, параллельно прямой L1.
Поскольку плоскость α2 проходит через прямую L2 , то она проходит также через точку M2(x2, y2, z2)=M2(6, −1, 2) и нормальный вектор n2=<m2, p2, l2> плоскости α2 перпендикулярна направляющему вектору q2 прямой L2. Тогда уравнение плоскости должна удовлетворять условию:
| A2x2+B2y2+C2z2+D2=0. | (44) |
а условие параллельности прямой L2 и искомой плоскости α2 представляется следующим условием:
| A2m2+B2p2+C2l2=0. | (45) |
Так как плоскость α2 должна быть параллельной прямой L1, то должна выполнятся условие:
| A2m1+B2p1+C2l1=0. | (46) |
| A1·6+B1·(−1)+C1·2+D1=0. | (47) |
| A1·2+B1·(−3)+C1·7=0. | (48) |
| A1·1+B1·3+C1·(−2)=0. | (49) |
Представим эти уравнения в матричном виде:
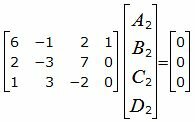 | (50) |
 | (51) |
Искомая плоскость может быть представлена формулой:
| A2x+B2y+C2z+D2=0. | (52) |
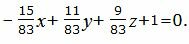 |
Упростим уравнение, умножив на число −83.
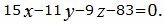 | (53) |
Расстояние между построенными плоскостями (43) и (53) будет расстоянием между прямыми (1) и (2).
Запишем формулы уравнений плоскостей α1 и α2 :
| A1x+B1y+C1z+D1=0. |
| A2x+B2y+C2z+D2=0. |
Поскольку нормальные векторы плоскостей α1 и α2 совпадают, то можно найти расстояние между плоскостями α1 и α2, используя следующую формулу:
 | (54) |
 |
Упростим и решим:
 |
Расстояние между прямыми равно: d=4.839339
📽️ Видео
19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Параллельные прямые (задачи).Скачать

Параллельные прямые. 6 класс.Скачать

Расстояние между параллельными прямымиСкачать

Параллельность прямых. 10 класс.Скачать

7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

№203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

7 класс, 24 урок, Определение параллельных прямыхСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. §13 геометрия 7 классСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Видеоурок "Расстояние между прямыми в пространстве"Скачать

6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать