Построение окружности с данным центром и данным радиусом (8 видео)

Построение окружности с данным центром и данным радиусом

С помощью линейки с делениями, циркуля, угольника, транспортира, лекал (рис. 313) вам не раз приходилось проводить различные геометрические построения.

А можно ли обходиться меньшим количеством чертёжных инструментов? Оказывается, что во многих случаях достаточно использовать только циркуль и линейку без делений . Например, чтобы провести биссектрису угла, совсем не обязательно иметь транспортир, а разделить отрезок пополам можно и тогда, когда на линейку не нанесена шкала.

А стоит ли в наше время, когда созданы точнейшие приборы и совершенные компьютерные программы, позволяющие выполнять сложнейшие измерения и построения, обходиться такими скудными средствами, как циркуль и линейка? На практике конечно нет. Поэтому, например, конструкторы, строители, архитекторы, дизайнеры не ограничивают себя в выборе инструментов.

Однако при построении фигур в геометрии принимают такие правила:

1) все построения выполняются только с помощью циркуля и ли нейки без делений ;

2) с помощью линейки можно через заданную точку провести произвольную прямую, а также через заданные две точки A и B провести прямую AB ;

3) с помощью циркуля можно построить окружность с данным центром и радиусом, равным заданному отрезку .

Итак, договоримся, что если в задаче требуется построить какую-то фигуру, то построение выполняется по описанным выше правилам.

Решить задачу на построение — это значит составить план ( алгоритм ) построения фигуры; реализовать план, выполнив построение; доказать, что полученная фигура является искомой.

Рассмотрим основные задачи на построение.

Задача 1. Постройте угол, равный данному, одна из сторон которого является данным лучом.

Решение. На рисунке 314 изображены угол A и луч OK . Надо построить угол, равный углу A , одной из сторон которого является луч OK .

Проведём окружность произвольного радиуса r с центром в точке A . Точки пересечения этой окружности со сторонами угла A обозначим B и С (рис. 315). Тогда AB = AC = r .

Проведём окружность радиуса r с центром в точке O . Она пересекает луч OK в точке M (рис. 316, a ). Затем проведём окружность с центром в точке M и радиусом BC . Пусть E и F — точки пересечения окружностей с центрами O и M (рис. 316, б ). Проведём лучи ОЕ и OF (рис. 316, в ).

Покажем, что каждый из углов EOM и FOM — искомый. Докажем, например, что ∠ EOM = ∠ BAC .

Рассмотрим треугольники ABC (рис. 315) и OEM (рис. 316, в ). Имеем: AB = OE = r = AC = OM . Кроме того, по построению EM = BC . Следовательно, треугольники ABC и OEM равны по третьему признаку равенства треугольников. Отсюда ∠ EOM = ∠ BAC . Аналогично можно показать, что ∠ BAC = ∠ FOM .

Замечание. Мы построили два угла ЕОМ и FOM , удовлетворяющие условию задачи. Эти углы равны. В таких случаях считают, что задача на построение имеет одно решение.

Задача 2. Постройте серединный перпендикуляр данного отрезка.

Решение. Пусть AB — данный отрезок (рис. 317, а ). Проведём две окружности с центрами A и B и радиусом AB . Точки пересечения этих окружностей обозначим M и N (рис. 317, б ). Проведём прямую MN (рис. 317, в ).

Из построения следует, что MA = MB = AB и NA = NB = AB (рис. 317, г ). Следовательно, точки M и N принадлежат серединному перпендикуляру отрезка AB . Прямая MN и является серединным перпендикуляром отрезка AB .

Содержание

Планиметрия (прямая и окружность)
1.1 Построить угол 60° с заданой стороной
1.2 Построить серединный перпендикуляр к отрезку
1.3 Середина отрезка
1.4 Окружность, вписанная в квадрат
1.6 Найти центр окружности
1.7 Квадрат, вписанный в окружность
Задача Наполеона
Круг. Окружность (центр, радиус, диаметр)
🔥 Видео

Видео:Окружность данного радиуса, проходящей через две заданные точкиСкачать

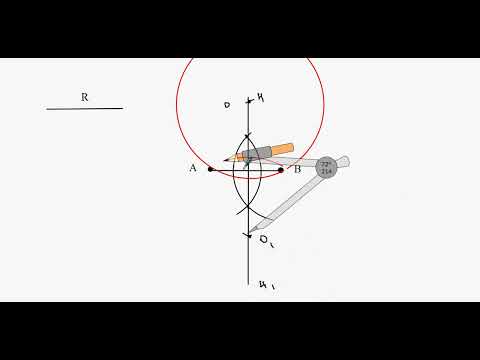
Планиметрия (прямая и окружность)

Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела (кроме 1.5) приложения Euclidea (геометрические построения с помощью циркуля и линейки).

Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.

1.1 Построить угол 60° с заданой стороной

1.2 Построить серединный перпендикуляр к отрезку

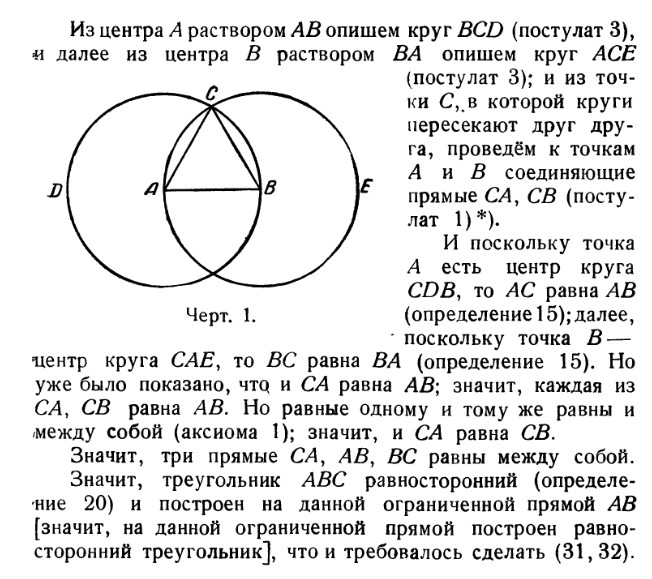
На данной ограниченной прямой построить равносторонний треугольник

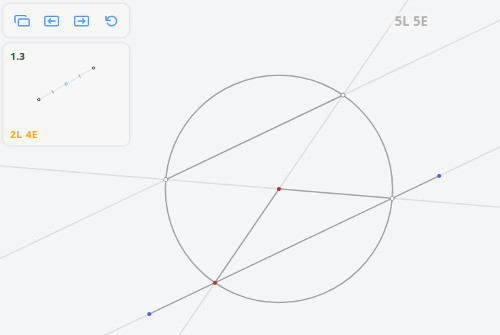
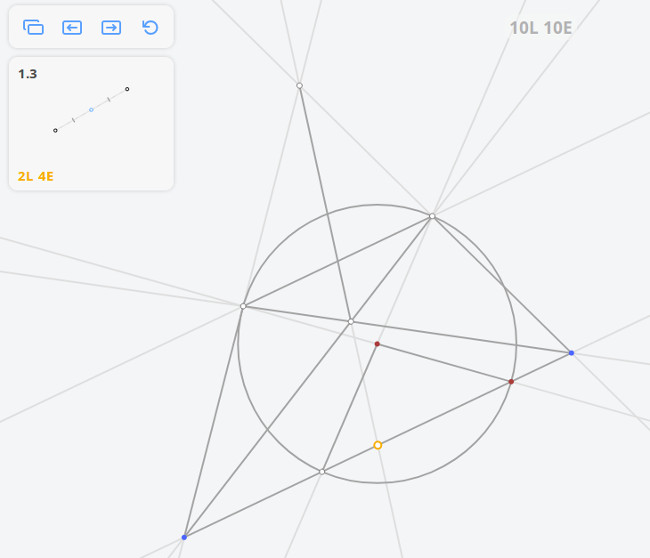
1.3 Середина отрезка

всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.

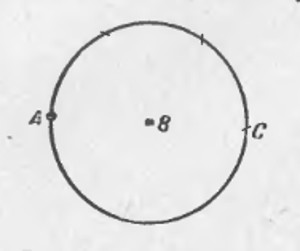
Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.

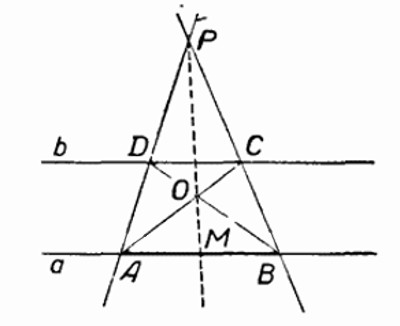
любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.

Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.

Решением задачи 1.3 по методу Штейнера-Понеселе будет:

1.4 Окружность, вписанная в квадрат

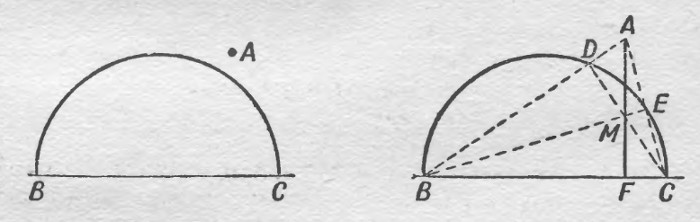
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.

Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.

И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой

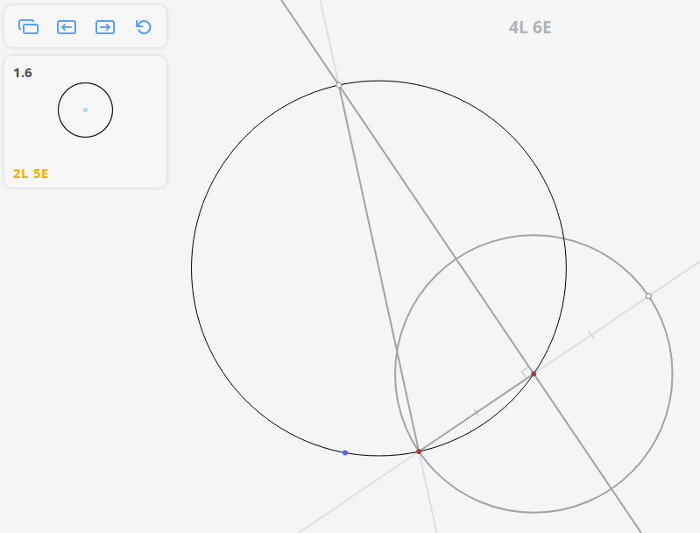
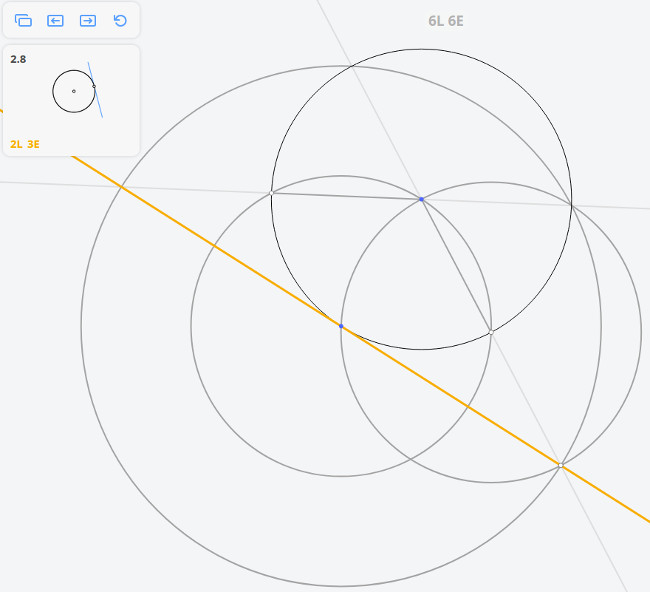
1.6 Найти центр окружности

Плоский угол, опирающийся на диаметр окружности, — прямой.

Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

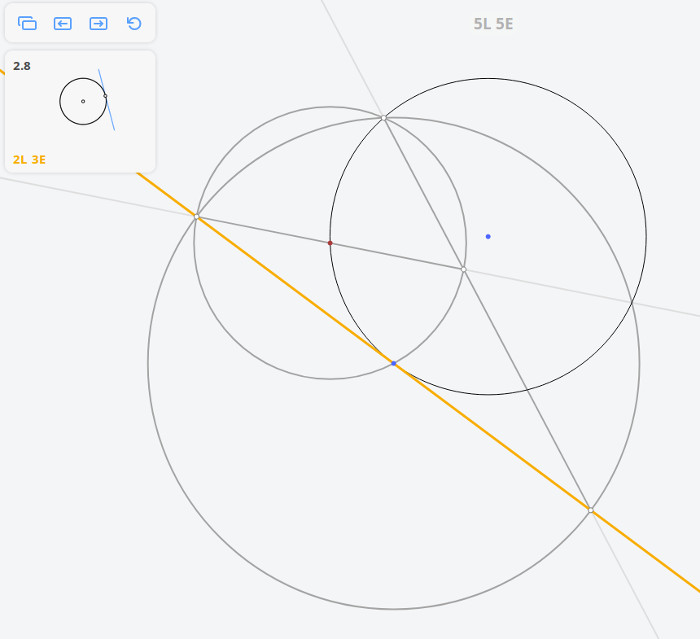
Рассмотрим задачу 2.8
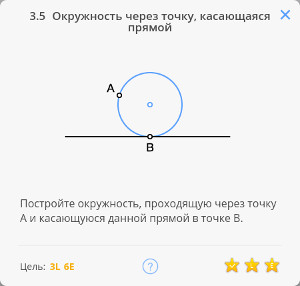
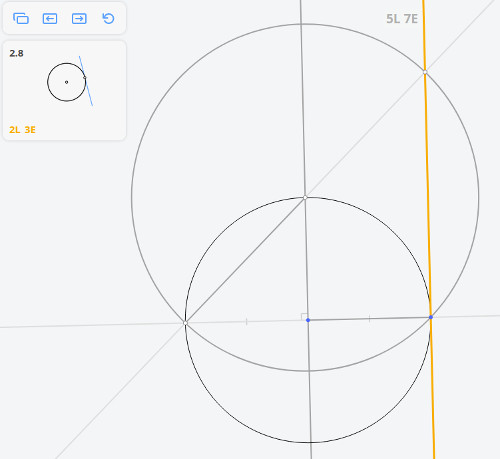
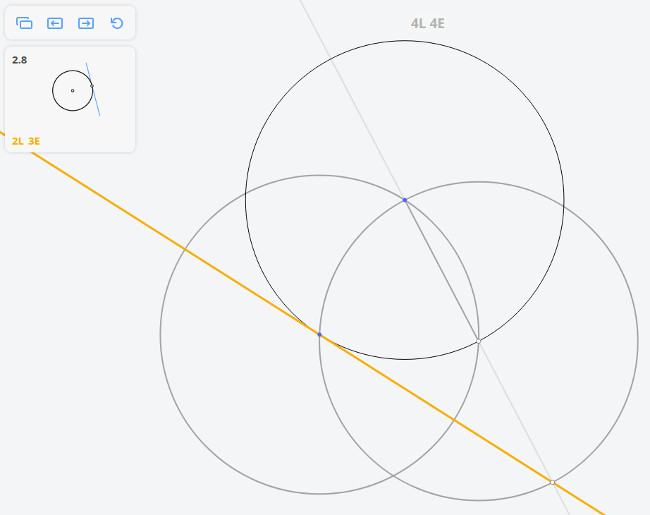
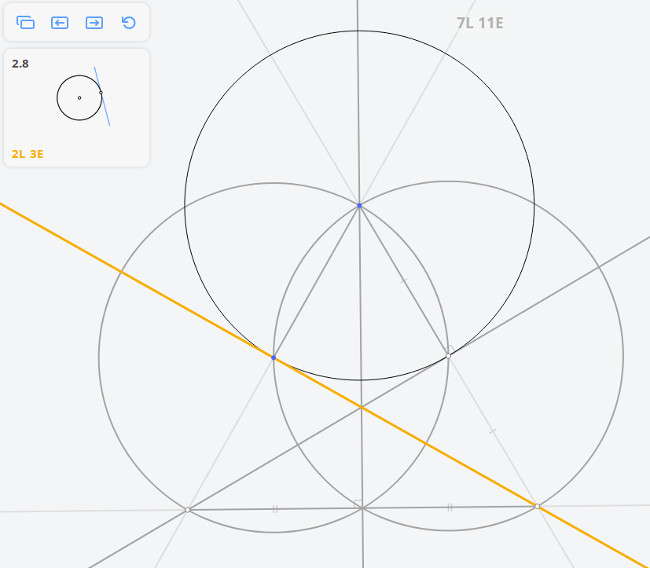
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса

Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.

Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка

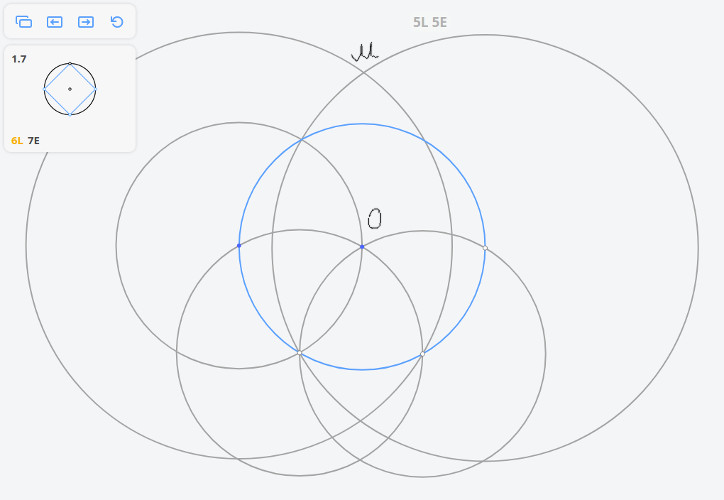
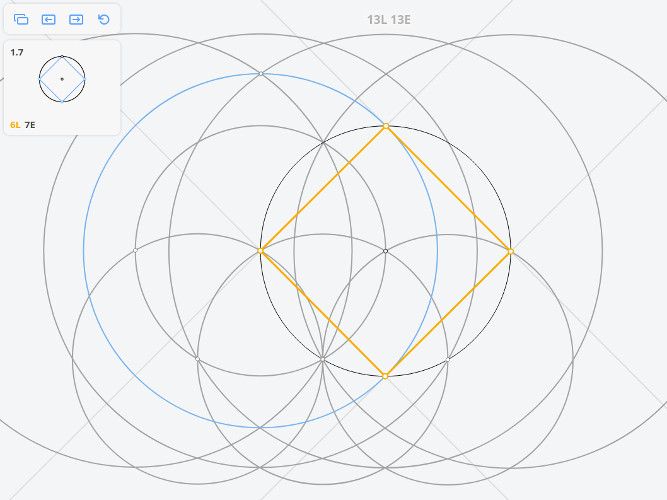
1.7 Квадрат, вписанный в окружность

Задача Наполеона

Решим задачу методом Мора-Маскерони.
Построим три окружности радиусом r и две окружности радиусом

В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом

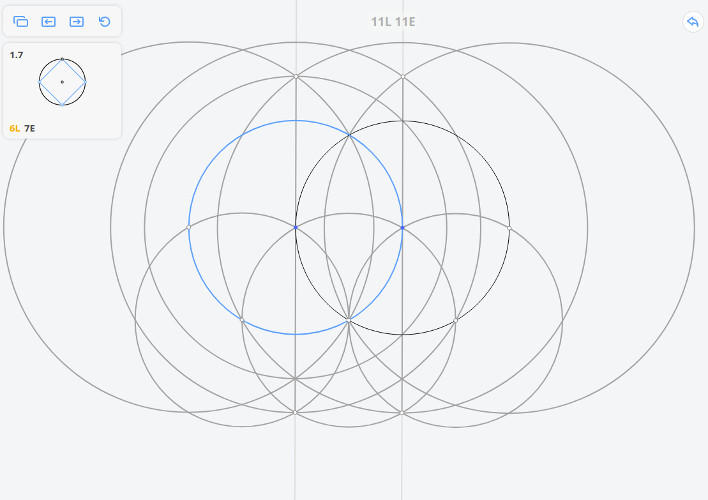
Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО

Видео:Найти центр и радиус окружностиСкачать

Круг. Окружность (центр, радиус, диаметр)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Данный урок посвящён изучению окружности и круга. Также учитель научит отличать замкнутые и незамкнутые линии. Вы познакомитесь с основными свойствами окружности: центром, радиусом и диаметром. Выучите их определения. Научитесь определять радиус, если известен диаметр, и наоборот.