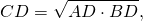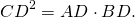В данной публикации мы рассмотрим, с помощью какой формулы можно найти среднее геометрическое чисел, а также разберем примеры задач для ее демонстрации на практике.
Видео:КАК НАЙТИ СРЕДНЕЕ ГЕОМЕТРИЧЕСКОЕ? ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать
Расчет среднего геометрического
Чтобы вычислить среднее геометрическое двух или более чисел, требуется их перемножить, а затем из полученного результата извлечь корень, степень которого равняется их количеству.
Допустим, у нас есть числа . Среднее геометрическое находится по формуле:
Частные случаи формулы:
<table data-id="257" data-view-id="257_15016" data-title="Среднее геометрическое" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value="
» data-order=»«>
<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value="
» data-order=»«>
<td data-cell-id="B4" data-x="1" data-y="4" data-db-index="4" data-cell-type="text" data-original-value="
» data-order=»«>
Видео:Среднее пропорциональное!? А что это!?Скачать
Пример задачи
Задание 1
Найдем среднее геометрическое чисел 3, 6 и 12.
Решение:
Воспользуемся соответствующей формулой для трех чисел:
Задание 2
Среднее геометрическое четырех чисел равняется 4, а также известны три из них – 2, 2 и 4. Найдем четвертое.
Решение:
Обозначим число, которое требуется найти буквой x . Формула выглядит следующим образом:
Помещаем число 4 под знак корня, сохранив равенство (для этого возводим его в четвертую степень, т.е. ):
Видео:Математика | Метрические соотношения в прямоугольном треугольникеСкачать
Проекции катетов на гипотенузу
Так как высота, проведенная к гипотенузе, представляет собой проведенный к ней перпендикуляр, то катеты — это наклонные, а отрезки гипотенузы, на которые делит ее высота — проекции катетов на гипотенузу прямоугольного треугольника.
В треугольнике ABC, изображенном на рисунке, AD — проекция катета AC на гипотенузу AB, BD — проекция катета BC на гипотенузу.
Катеты, их проекции на гипотенузу, гипотенуза и высота прямоугольного треугольника связаны между собой формулами.
1) Свойство высоты, проведенной к гипотенузе.
Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.
2) Свойства катетов прямоугольного треугольника.
Катет прямоугольного треугольника есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.
Видео:Вариант 52, № 2. Среднее пропорциональное (среднее геометрическое) в прямоугольном треугольникеСкачать
Прямоугольный треугольник
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом занятии, посвященном прямоугольному треугольнику, мы еще раз вспомним все то, что изучали ранее. Дадим определение прямоугольному треугольнику – треугольнику с одним углом в 90°. Рассмотрим, как обозначается такая фигура, запишем основные тригонометрические функции.
🎦 Видео
Задача, которую исключили из экзамена в АмерикеСкачать
Тема 6. Среднее пропорциональное (среднее геометрическое) в прямоугольном треугольникеСкачать
пропорциональные отрезки в ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ 8 классСкачать
8 класс, 26 урок, Пропорциональные отрезки в прямоугольном треугольникеСкачать
Подобие прямоугольных треугольников. Среднее геометрическое (пропорциональное). Геометрия 8-9 классСкачать
Задача, которую не запретили в школах. Делим треугольник Как построить среднее геометрическоеСкачать
РАЗБИРАЕМ СРЕДНЕЕ ГЕОМЕТРИЧЕСКОЕ ЧАСТЬ II #shorts #математика #егэ #огэ #профильныйегэСкачать
Задачи на среднее геометрическое (пропорциональное). Геометрия 8 9 классСкачать
Высота как среднее геометрическое отрезков | Профильная математикаСкачать
Хитрый периметрСкачать
Геометрия 8 класс (Урок№19 - Пропорциональные отрезки в прямоугольном треугольнике.)Скачать
6. Среднее пропорциональное (среднее геометрическое) в прямоугольном треугольникеСкачать
Пропорциональные отрезки в прямоугольном треугольнике. Видеоурок 14. Геометрия 8 классСкачать
Геометрия.Прямоугольный треугольник. Пропорциональные отрезки в прямоугольном треугольникеСкачать
Высота в прямоугольном треугольнике. 8 класс.Скачать
Метрические соотношения в прямоугольном треугольнике. 1 часть. 9 класс.Скачать
