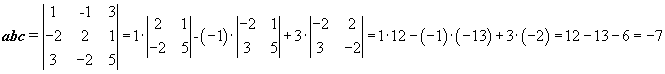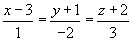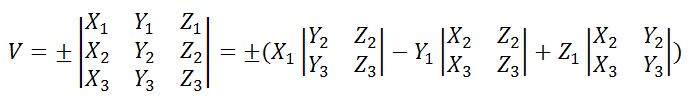Найти объем параллелепипеда построенного векторах (4 видео)

Найти объем параллелепипеда построенного векторах

№ 1
Найти объём параллелепипеда, построенного на векторах , , .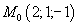

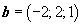
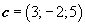
Решение

Объём параллелепипеда, построенного на векторах a, b, c численно равен модулю смешанного произведения этих векторов.

V = | abc |

V = | -7 | = 7

№ 2
Найти объём пирамиды, построенной на векторах , , .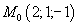

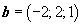
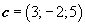
Решение

Объём пирамиды, построенной на векторах a, b, c равен 1/6 объёма параллелепипеда, построенного на этих векторах.

V = | abc |/6

V = | -7 | /6= 7/6

№ 3

Найти объём тетраэдра ABCD.

Решение

Построим векторы AB, AC, AD.

, , .

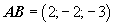
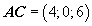
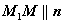
Объём тетраэдра, построенного на векторах AB, AC, AD равен 1/6 объёма параллелепипеда, построенного на этих векторах.

Объём параллелепипеда, построенного на векторах AB, AC, AD численно равен модулю смешанного произведения этих векторов.

V = | AB · AC· AD |/6

V = | 12 | /6 = 12/6 = 2

Видео:Решение, вычислите объем параллелепипеда, построенного на векторах a, b, c пример 4Скачать

Объём параллелепипеда

Объём параллелепипеда, построенного на трех векторах

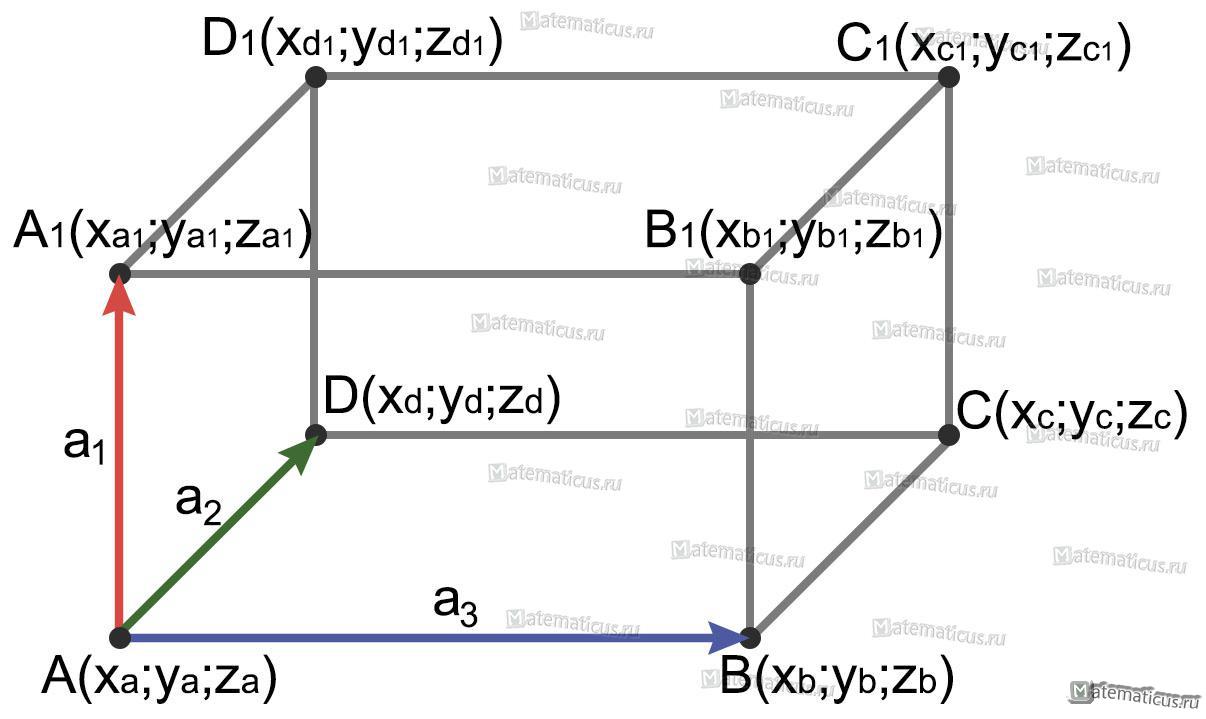
где координаты векторов в соответствии с рисунком

вычисляются следующим образом

Знак плюс берется, когда определитель третьего порядка положителен, а минус наоборот – знак отрицателен.

Найти объём параллелепипеда, построенного на векторах a₁=, a₂= и a₃=

$ = pm left( <2cdotleft( <left( right)cdot2 — 1cdot3> right) — 3left( <left( right)cdot2 — 3cdot3> right) + 2left( <left( right)cdot1 — 3cdotleft( right)> right)> right) = -33$

Так как определитель отрицателен, берем перед ним знак « − ».

Тогда объём параллелепипеда построенного на векторах равен V=33

Видео:Площадь параллелограмма, построенного на данных векторахСкачать

Вектор. Смешанное произведение векторов.

Также его называют тройным скалярным произведением векторов, скорее всего это связано с тем,

что результат — это скаляр (точнее — псевдоскаляр).

Смешанное произведение векторов — скалярное произведение вектора на векторное произведение векторов и .

Или другими словами:

Смешанным произведением векторов является число , состоящее из скалярного произведения вектора на векторное произведение векторов и . Смешанное произведение

векторов записывается следующим образом:

Геометрический смысл смешанного произведения векторов.

Геометрический смысл смешанного произведения векторов: если три вектора правые, то их

смешанное произведение равно объему параллелепипеда построенного на них:

В случае левой тройки , смешанное произведение указанных векторов равно объему

параллелепипеда со знаком “–“:

Если , и компланарны, то их смешанное произведение = 0.

Вывод: объем параллелепипеда, построенного на векторах , и равен модулю смешанного

произведения этих векторов:

Объем пирамиды, построенной на этой тройке этих векторов, находим по формуле:

Геометрические свойства смешанного произведения векторов.

1. Модуль смешанного произведения некомпланарных векторов равен объему

параллелепипеда, построенного на этих векторах. Произведение будет со знаком плюс, если

тройка векторов — правая, и будем иметь отрицательный знак, если тройка — левая,

2. Смешанное произведение =0 тогда и только тогда, когда векторы компланарны:

векторы компланарны.

Алгебраические свойства смешанного произведения векторов.

1. При перемене мест двух множителей смешанное произведение меняет знак на противоположный:

При циклической (круговой) перестановке множителей смешанное произведение остается без изменений:

2. Смешанное произведение линейно по любому множителю.

Первое свойство следует из первого геометрического свойства и свойств ориентации троек векторов, так

как от перестановки двух множителей местами, модуль смешанного произведения остается прежним, а

изменяется только ориентация тройки. При циклической перестановке векторов ориентация тройки

остается без изменений.

Второе свойство следует из линейности скалярного произведения и первого свойства.

Формула вычисления смешанного произведения векторов.

Теорема (формула вычисления смешанного произведения векторов):

Если у векторов в правом ортонормированном базисе координаты, ,

соответственно, то смешанное произведение их вычисляется по следующей формуле:

Из определения следует:

что и требовалось доказать.

Еще некоторые свойства смешанного произведения векторов.

3 .Три вектора компланарны в том случае, если

4. Тройка векторов будет правой только если . Ежели , то векторы, и

создают левую тройку векторов.

10. Тождество Якоби:

Если векторы , и заданы своими координатами, то их

смешанное произведение можно найти по формуле, приведенной ниже:

🎬 Видео

§20 Нахождение объёма параллелипипедаСкачать

Найдите площадь параллелограмма, построенного на векторахСкачать

Решение, найдите объем параллелепипеда, построенной на векторах a, b, c пример 7. Высшая математикаСкачать

Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

как найти площадь параллелограмма построенного на векторахСкачать

Найдите длины диагоналей параллелограмма, построенного на векторах a=(1;-1;-4) и b=(-5;3;8)Скачать

Решение, вычислить объем параллелепипеда, построенного на векторах a, b, c пример 11Скачать

Площадь параллелограмма по векторамСкачать

Задача 4. Вычислить площадь параллелограмма, построенного на векторах.Скачать

Площадь треугольника, построенного на векторахСкачать

Найти угол между векторами и площадь параллелограмма, построенного на этих векторахСкачать

Высшая математика. 4 урок. Аналитическая геометрия. Вычисление объема тетраэдра.Скачать

1. Векторы и параллелограмм задачи №1Скачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Решение, найти высоту параллелепипеда, построенного на векторах a, b, c пример 17 Высшая математикаСкачать

Как найти объем. Принцип Кавальери | Ботай со мной #050 | Борис Трушин |Скачать

Нахождение объема параллелепипеда, построенного на векторах а, b и с. пример 2Скачать